Лекция 22

22. Криволинейные интегралы

22.1. Определение и существование криволинейного интеграла 2-го рода

Пусть в некоторой области D задано плоское силовое поле. Т. е. в области D вектор силы задается формулой:

F=P(x,y) i+Q(x,y) j=(P(x,y);Q(x,y)).

Проведем в области D некоторый контур AB. Разобьем контур на достаточно большое число достаточно малых частей системой точек A=M₀,M₁,M₂,...,M_n=B. На каждом элементарном перемещении вычислим значения

P(x_i ,y_i ) x_i + Q(x_i ,y_i )y_i

и просуммируем полученные значения.

(1)

Обозначим = maxM_i-1M_i . Начнем строить различные интегральные суммы так, чтобы 0 и, соответственно, n.

Определение. Предел интегральных сумм вида (1) при 0, если этот предел существует и не зависит ни от способа разбиения контура L на части, ни от выбора значений M_i(_i,_i) L_i на этих частях, называется криволинейным интегралом 2-го рода по контуру AB. Обозначается

(2)

Теорема. Если функция z=f(x,y) непрерывна в области D и область D ограничена, то интеграл (2) существует. (Без доказательства).

22.2. Свойства криволинейного интеграла 2-го рода

Свойства криволинейного интеграла 2-го рода аналогичны общим свойствам интегралов. Поэтому отметим отличительные свойства. Пусть указанные интегралы существуют. Тогда выполняются следующие свойства.

1. Постоянный сомножитель можно выносить за знак криволинейного интеграла по контуру AB от каждого из слагаемых.

2. При изменении направления движения по контуру знак интеграла изменяется на противоположный.

3. Если контур AB разбить на два контура AC и CB, не имеющие общих внутренних точек, то

Это правило верно и для случая любого числа частей.

Разобрать доказательство по учебнику самостоятельно.

22.3. Вычисление криволинейного интеграла 2-го рода

Пусть нам дан интеграл (2). Рассмотрим случай, когда контур задан параметрически

Тогда

(3)

(Без доказательства)

Если контур задан в явном виде с помощью кривой, то можно свести этот случай к параметрическому, считая

Тогда

Пример. Вычислить

22.4. Определение и существование криволинейного интеграла 1-го рода

Пусть в некоторой области D задана z=f(x,y). Проведем в области D некоторый контур AB. Разобьем контур на достаточно большое число достаточно малых частей системой точек A=M₀,M₁,M₂,...,M_n=B. На каждом элементарном перемещении вычислим значения z=f(x_i,y_i). Найдем элементарную длину контура

вычислим произведения f (x_i,y_i)s_i и просуммируем полученные значения.

(4)

Обозначим = maxM_i-1M_i . Начнем строить различные интегральные суммы так, чтобы 0 и, соответственно, n.

Определение. Предел интегральных сумм вида (1) при 0, если этот предел существует и не зависит ни от способа разбиения контура L на части, ни от выбора значений M_i(_i,_i) L_i на этих частях, называется криволинейным интегралом 2-го рода по контуру AB. Обозначается

(5)

Теорема. Если функция z=f(x,y) непрерывна в области D и область D ограничена, то интеграл (2) существует. (Без доказательства).

22.5. Свойства криволинейного интеграла 1-го рода

Свойства криволинейного интеграла 1-го рода аналогичны общим свойствам интегралов. Поэтому отметим отличительные свойства. Пусть указанные интегралы существуют. Тогда выполняются следующие свойства.

1. При изменении направления движения по контуру величина интеграла не изменяется.

2. Если контур AB разбить на два контура AC и CB, не имеющие общих внутренних точек, то

Это правило верно и для случая любого числа частей.

Разобрать доказательство по учебнику самостоятельно.

22.6. Вычисление криволинейного интеграла 1-го рода

Пусть нам дан интеграл (2). Рассмотрим случай, когда контур задан параметрически

Тогда

(Без доказательства)

Если контур задан в явном виде с помощью кривой , то можно свести этот случай к параметрическому, считая

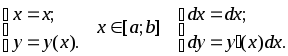
Тогда

22.7. Криволинейные интегралы по замкнутому контуру

Если начало и конец контура совпадают, то контур называется замкнутым. Пусть нам дан криволинейный интеграл по замкнутому контуру. Разобьем контур на две части точками и . Тогда

Для криволинейного интеграла 2-го рода по замкнутому контуру нужно различать направление обхода. Будем считать направление обхода положительным, если при движении вдоль контура область остается слева. Противоположное направление обхода является отрицательным.

22.8. Формула Грина

Теорема. Если область D ограничена замкнутым контуром и функции z=P(x,y) и z=Q(x,y) непрерывна в области D, включая границу, то

Доказательство. Рассмотрим область D и обозначим уравнения границ контура

Вторая часть равенства доказывается аналогично.

Пример. Вычислить

где контур треугольника с вершинами

Решение. Применим формулу Грина

22.9. Криволинейные интегралы по контурам в пространстве

Контур может быть задан и в пространстве. Пусть в некоторой области заданы функции и некоторый контур. Тогда

Тогда криволинейный интеграл 2-го рода равен

Криволинейный интеграл 1-го рода равен