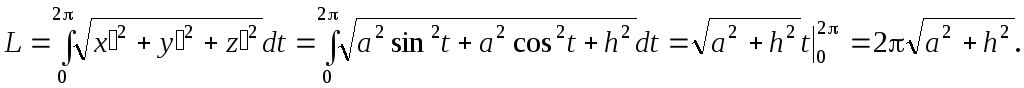Лекция 8

8. Геометрические приложения определенного интеграла

8.1. Вычисление площадей плоских фигур

8.1.1 Площадь плоских фигур в декартовых координатах

Если на интервале [a,b] задана непрерывная функция y=f(x), причем f(x)0 и a<b, то из геометрической иллюстрации видим, что

(1)

где S площадь криволинейной трапеции, ограниченной снизу осью Ox, с боков прямыми x=a и x=b и сверху графиком функции y=f(x) (см. рис. 1)

y

y=f(x)

O a b x

Рис. 1. Вычисление площади криволинейной трапеции

Если условие f(x)0 не выполняется, то нужно разбить интервал [a,b] на части корнями уравнения f(x)=0, выделить интервалы знакопостоянства функции, вычислить интегралы на каждом из интервалов и просуммировать по модулю полученные значения. Получим площадь фигуры, ограниченной осью Ox и графиком функции y=f(x), с боков прямыми x=a и x=b.

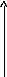y

y=f(x)

O a b x

y=g(x)

Рис. 2. Вычисление площади криволинейной фигуры

Пусть на интервале [a,b] заданы непрерывные функции y=f(x) и y=g(x), причем f(x) g(x) для x[a,b]. Если нужно найти площадь фигуры, ограниченной с боков прямыми x=a и x=b и графиками функций y=f(x) и y=g(x), то (см. рис.2) площадь равна

(2)

Пример

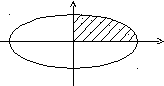
Вычислить площадь (рис. 3), заключенную внутри эллипса

y

O a x

Рис. 3. Площадь эллипса

Уравнение части эллипса, удовлетворяющей условию x0, y0 можно записать в виде

Площадь четверти эллипса равна

Полная площадь эллипса равна S=ab.

Пример.

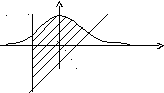
Вычислить площадь, заключенную между линиями

y

y=x - 0,5

-1 1 x

Рис. 4. Вычисление площади фигуры

Изобразим линии на рис. 4. Найдем точку пересечения

Площадь равна

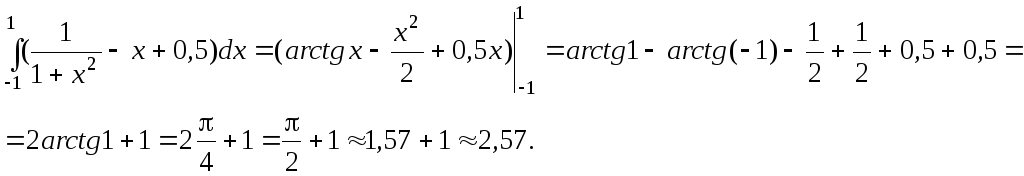
8.1.2. Площадь плоских фигур, ограниченных кривыми, заданными параметрически

Пусть нужно найти площадь криволинейной трапеции вида (1), где функция задана параметрически

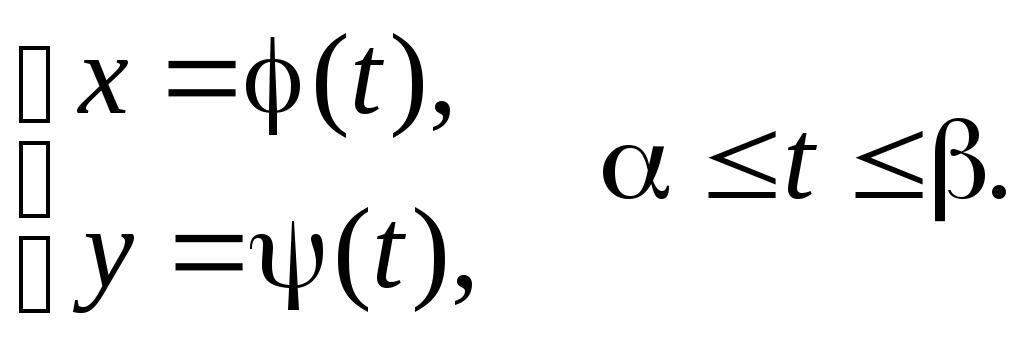
Пусть, для определенности ()=a; ()=b и a<b. Исключим параметр t. Получим функцию вида y=y(x). Если на интервале [a,b] дана функция y= y(x) 0, то площадь равна

Вернемся к параметру t. Тогда

Пример

Вычислить площадь, ограниченную кривой

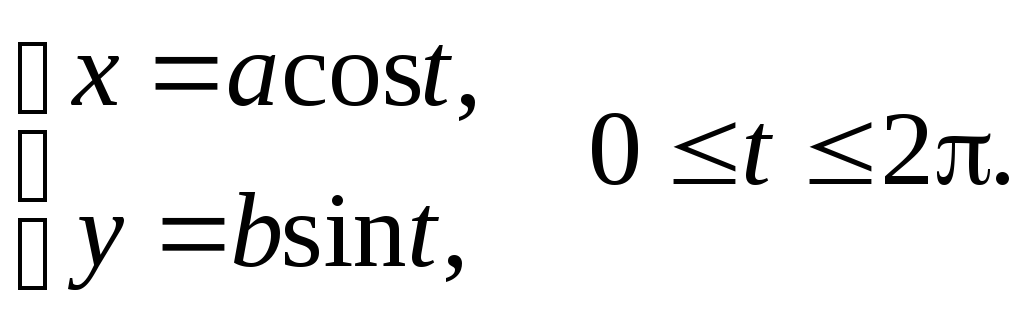
Уравнение задает кривую, которая называется эллипсом. Тогда площадь верхней половины равна

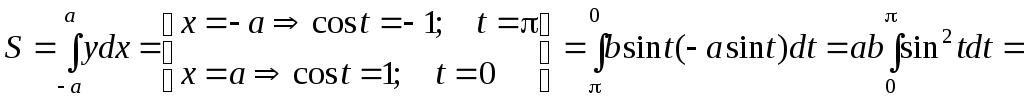
Полная площадь эллипса равна удвоенной величине S=ab. Изображение кривой дано на рис. 3. Результат совпадает с полученным выше в примере. При a=b эллипс является окружностью и S=a².

8.1.3 Площадь криволинейного сектора в полярных координатах

Пусть в полярных координатах задана кривая r=r() при . Проведем лучи = и =. Получим криволинейный сектор. Разобьем интервал [;] на части системой точек =₀,₁,₂,...,_n= и проведем лучи =  _i. Криволинейный сектор разобьется на элементарные секторы. Обозначим  _i=  _i-  _i-1, тогда площадь элементарного сектора S _i приближенно равна площади элементарного кругового сектора S_i 1/2 r_i² _i. Площадь сектора приближенно равна сумме элементарных секторов. Перейдем к пределу при 0. Получим (см. рис. 5) площадь криволинейного сектора, заданного с помощью полярных координат

Замечание: при вычислении этой площади предполагается, что величины углов измеряются в радианах.

= _n  _i

 _{i -1}

 ₁

  ₀= 



Рис. 5. Площадь криволинейного сектора

Пример

Вычислить площадь, ограниченную кривой:

Фигура называется кардиоидой. Ее график дан в лекции 22 рис.15. Она обладает симметрий относительно оси Ox. Поэтому вычислим площадь половины фигуры и удвоим ее. Пределы изменения [0,]

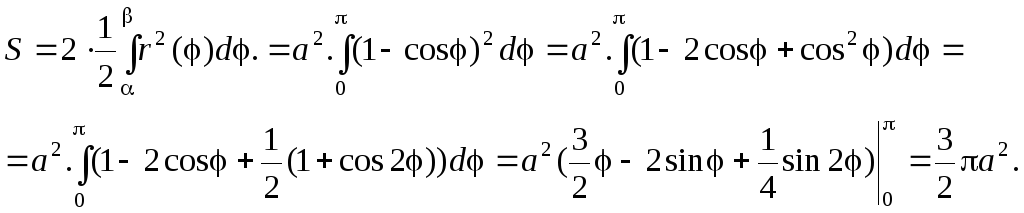
8.2. Длина кривой

8.2.1 Длина дуги в декартовых координатах

Пусть на интервале [a,b] задана непрерывно дифференцируемая функция y=f(x). Ее график является некоторой гладкой кривой. Разобьем интервал [a,b] на части системой точек a =x₀, x₁, x₂, ... ,x_n-1, x_n =b, вычислим y_i=f(x_i) и построим систему точек M_i(x_i,y_i). Интервал [a,b] разобьется на достаточно малые части. Обозначим x_i=x_i- x_i-1, y_i=y_i- y_i-1. Соединим каждую пару соседних точек отрезком M_i-1M_i. В результате в кривую впишется ломаная M₀M₁M₂...M_n. Обозначим длину отрезка M_i-1M_i через l_i

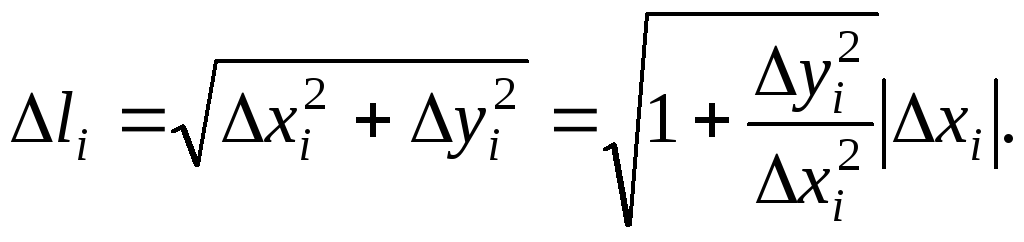
y M_i-1

M₁ M_i

M₀

M_n

O x

Рис. 5. Вычисление длины дуги кривой

Будем считать, что x _i > 0. Длина отрезка кривой L приближенно равна длине ломаной. Перейдем к пределу при 0.

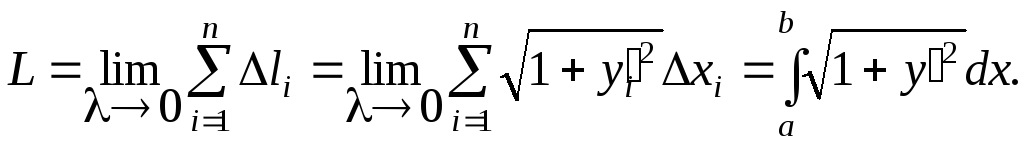
Пример

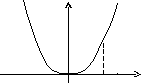
Вычислить длину кривой y=0,5x² при x[0,2]. Изобразим линию на рис. 6.

y

y=0,5x²

O 2 x

Рис. 6. График кривой y=0,5x²

Найдем

Перенесем интеграл из правой части в левую

Длина кривой равна

8.2.2. Длина дуги кривой, заданной параметрически

Пусть нужно найти длину кривой для функции, заданной параметрически

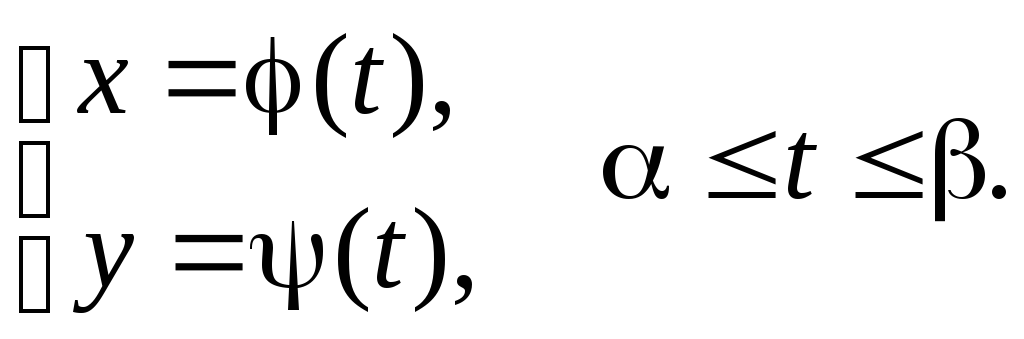
Пусть, для определенности ()=a; ()=b и a<b. Исключим параметр t. Получим функцию вида y=y(x).

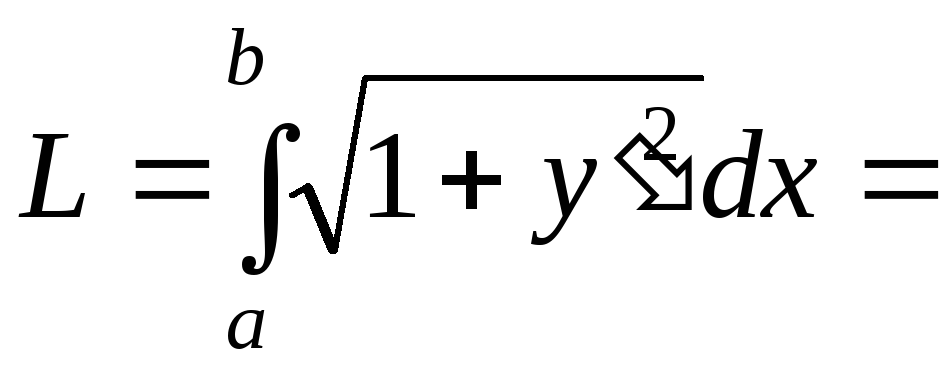
Вернемся к параметру t. Тогда

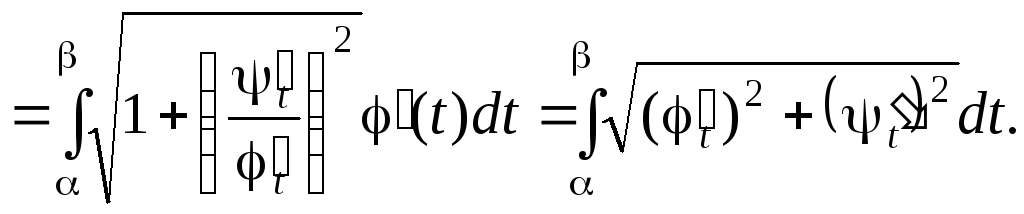
Пример

Вычислить длину витка винтовой линии

Длина равна