Лекция 18

18. Функциональные ряды

18.1. Понятие функционального ряда

Пусть задана последовательность функций вида

Функциональным рядом называется выражение

(1)

Областью определения ряда называется множество значений переменной x, при которых определены все члены ряда. Возьмем некоторое значение и подставим его в ряд (1) получим числовой ряд. Этот ряд может сходиться, а может и расходиться. Множество значений переменной x, для которых ряд (1) сходится называется областью сходимости ряда. Определение области сходимости - сложная задача и мы ограничимся лишь упоминанием о ней. В области сходимости ряда сумма ряда является некоторой функцией, которую мы обозначим S(x). Определяется она так же, как и для числового ряда. Введем частичную сумму из n первых членов ряда.

Определение. Предел последовательности s_n, если он существует, называется суммой ряда (1).

(2)

Отбросим n первых членов ряда (1). Оставшийся ряд называется остатком и обозначается r_n. Т. е.

Теорема. Для того чтобы ряд сходился необходимо и достаточно, чтобы при n сумма остатка ряда стремилась к нулю.

Без доказательства.

Пример. Рассмотрим ряд

Этот ряд является геометрической прогрессией, у которой

При x0 выполняется условие 0<q<1. И сумма ряда равна S(x)=1. При x=0 сумма ряда равна S(0)=0. Область сходимости ряда - вся числовая ось. Сумма ряда разрывная функция. Функция имеет разрыв при x=0.

Из данного примера видно, что обращаться с функциональными рядами так просто нельзя. В частности, если заменить ряд частичной суммой ряда, состоящего из непрерывных функций, получим непрерывную функцию. В то время как сумма функционального ряда может оказаться разрывной. Для того чтобы не возникали подобные неприятности, нужно ввести для функциональных рядов понятие равномерной сходимости.

Определение. Пусть сумма ряда равна S(x) на [a,b]. Функциональный ряд называется равномерно-сходящимся на [a,b], если для любого >0 существует номер N, такой что при всех n> N и всех x[a,b], выполняется неравенство

.

Данное определение носит абстрактный характер и пользоваться им не просто. Поэтому введем более простое понятие, которое является достаточным для равномерной сходимости.

Определение. Если для функционального ряда (1) существует сходящийся числовой ряд (2) с положительными членами

(2)

такой, что для всех n и всех x[a,b] выполняется неравенство

то говорят, что ряд (2) мажорирует ряд (1) на [a,b].

Пример. Ряд

мажорируется рядом на всей числовой оси, так как .

Теорема. Если ряд (2) мажорирует ряд (1) на [a,b], то ряд (1) сходится равномерно на [a,b]. (Без доказательства).

Замечание. Теорема дает достаточное условие равномерной сходимости, но не является необходимым.

Теорема. Если ряд (1) равномерно сходится на [a,b] и члены ряда непрерывные функции, то его сумма, также непрерывна. (Без доказательства).

Первый пример дает пример неравномерно-сходящегося ряда на любом интервале, содержащем 0. Второй пример - пример равномерно-сходящегося ряда на всей числовой оси.

Теорема. Если ряд (1) сходится на [a,b] и его сумма ограничена и члены ряда интегрируемые на [a,b] функции, то

т. е. возможно почленное интегрирование членов ряда. (Без доказательства).

Теорема. Если ряд (1) сходится на [a,b] и члены ряда дифференцируемые на [a,b] функции и ряд, составленный из производных сходится равномерно на [a,b], то

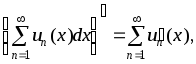
т. е. возможно почленное дифференцирование членов ряда. (Без доказательства).

18.2. Степенные ряды

Степенным рядом называется ряд вида

где a₀, a₁, a₂,..., a_n - const, x₀ - const.

Рассмотрим вначале более простой случай ряда, когда x₀=0.

(4)

Теорема Абеля. Если ряд (4) сходится при некотором значении x₀, то он сходится абсолютно для всех x, удовлетворяющих условию

(5)

Если ряд (4) расходится при некотором значении x₀, то он расходится для всех x, удовлетворяющих условию

.

Доказательство. Пусть ряд (4) сходится при некотором значении x₀. Это значит, что существует сумма ряда Следовательно, выполняется необходимый признак сходимости

Это значит, что для любого >0 существует номер N такой, что при всех n> N выполняется неравенство

Рассмотрим остаток ряда (4)

Из неравенства (5) следует, что

Тогда

Мы видим, что остаток ряда (4) мажорируется геометрической бесконечно-убывающей прогрессией. Следовательно, ряд (4) сходится. Первая часть теоремы доказана. Вторая часть доказывается аналогично. Разобрать самостоятельно.

Из теоремы Абеля следует, что область сходимости ряда (4) имеет вид -R<x<R, где R>0. При x>R ряд (4) расходится. Концы интервала x= -R и x=R могут входить, а могут и не входить в интервал сходимости. Если R=0, то область сходимости состоит из одной единственной точки x=0, Если R=, то область сходимости вся числовая ось (-;).

18.3. Исследование области сходимости степенных рядов

Для исследования сходимости наиболее удобно применять признак Даламбера или радикальный признак Коши. Пусть коэффициенты ряда не содержат нулевых значений и изменяются монотонно. Применим признак Даламбера

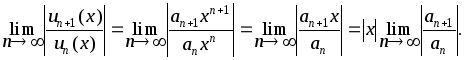
Если предел меньше 1, то ряд сходится, если предел больше 1, то ряд расходится. Пусть предел

Тогда ряд сходится при условии xl<1 или x<1/l=R. Откуда находим -R<x<R.

Пример. Исследовать область сходимости

Применим признак Даламбера

Ряд сходится, если

Исследуем концы. Положим x=2, получим

Получили гармонический ряд. Ряд расходится. Положим x=-2, получим

Получили знакочередующийся ряд. По признаку Лейбница ряд сходится. Следовательно, область сходимости ряда