Варианты задания №10

Найти точку минимума функции f(x) с точностью 0,1 указанным методом: а-оптимальн-пассивный поиск, б-метод деления отрезка пополам, в-метод золотого сечения.

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

31. 32.

33. 34.

35. 36.

37. 38.

39. 40.

Пример выполнения задания №10

Методом золотого сечения найти точку минимума функции с точностью 0.1

1. Находим отрезок локализации. При x=-1 имеем f(-1)=7, при x=0- f(0)=4, при x=1-f(1)=9. Следовательно, на отрезке [-1,1] имеется точка минимума. Полагаем a₀=-1, b₀=1.

2. Методом золотого сечения отрезка находим две точки:

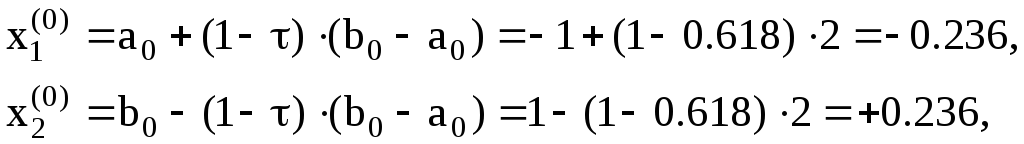
1. Вычисляем значения функции в этих точках:

2. Так как , то точка минимума находится на отрезке.

3. Имеем новый отрезок локализации

4. Определяем длину l₁ отрезка [a₁,b₁]

.

5. Так как l₁=1.236>0.1, то на отрезке [a₁,b₁] методом золотого сечения находим две точки

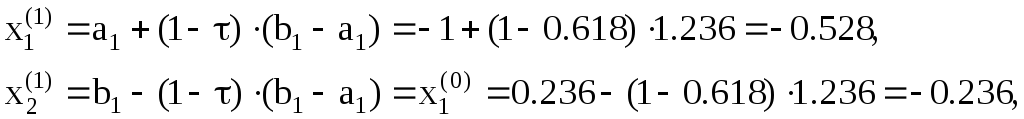6. Вычисляем значение функции в новой точке . В точкезначение функции уже известно. Имеем

7. Так как , то точка минимума находится на отрезке.

8. Имеем новый отрезок локализации

9. Определяем длину l₂ отрезка [a₂,b₂]

.

10. Так как l₂>0.1, то на отрезке [a₂,b₂] методом золотого сечения находим две точки и т.д. В результате получаем

11. Следовательно, точка минимума приблизительно равна

12. Вычисляем значение функции в этой точке

VIII. Методы многомерной оптимизации

1. Основные определения. Задачей многомерной оптимизации является минимизация функции U=f(x₁,x₂,...,x_m) от m переменных (параметров) x₁,x₂,...,x_m. Если нет ограничений на параметры x₁,...,x_m, то говорят о глобальной безусловной минимизации, если есть ограничения на параметры x₁,...,x_m, то говорят об условной минимизации.

Для сокращенного обозначения функции многих переменных удобно использовать векторное обозначение , при этом подразумевается, что каждой величинесопоставлен свой единственный набор значений величинx₁,...,x_m. В соответствии с этим величину можно рассматривать как точку (элемент)m-мерного линейного пространства независимых переменных x₁,...,x_m. Если в этом пространстве ввести единичные векторы , поставленные в соответствие переменнымx₁,...,x_m, то величину можно рассматривать как вектор:, а операции сложения и вычитания производить по правилу векторов.

а) поверхность уровня. Множество точек , для которых называется поверхностью уровня, для двух переменных это множество называется линей уровня

б) градиент. Вектор называется градиентом функциии обозначается:

(8.1)

Векторуказывает направление наискорейшего возрастания функции, а векторназывается антиградиентом и указывает направление наискорейшего убывания функции. Градиент всегда перпендикулярен поверхности (линии) уровня.

2. Необходимое и достаточное условия минимума функции многих переменных:

а) необходимое условие. Необходимым условием минимума функции многих переменных является условие равенства нулю ее градиента:

(8.2)

или

б) достаточное условие. Достаточным условием является условие положительной определенности матриц Гессе:

(8.3)

Для положительной определенности матрица Гесса необходимо, чтобы ее собственные числа ₁,...,_m были положительны. Собственные числа ₁,...,_m являются корнями характеристического уравнения:

(8.4)

где det -определитель квадратной матрицы ранга m, Е - единичная матрица.

Матрица C=G-E называется характеристической матрицей для матрицы G.