
- •«Вычислительная математика»
- •2. Погрешности арифметических операций. Правила оценки погрешностей.
- •Варианты задания №1.
- •Пример выполнения задания №1.
- •Варианты задания №2.
- •Пример выполнения задания №2.
- •Варианты задания №3.
- •Пример выполнения задания №3.
- •Варианты задания №4.
- •Пример выполнения задания №4.
- •Варианты задания №5.
- •Пример выполнения задания №5.
- •IV. Численное интегрирование.
- •Варианты задания №6.
- •Пример выполнения задания №6.
- •V. Системы линейных алгебраических уравнений.
- •Варианты задания №7
- •Пример выполнения задания №7.
- •Пример выполнения задания №8
- •VI. Решения нелинейных уравнений.
- •§3. Метод Ньютона для системы нелинейных уравнений. Пусть имеется следующая система нелинейных уравнений:
- •Варианты задания №9
- •Пример выполнения задания №9
- •VII. Нахождение минимума функций одной переменной.
- •2. Методы прямого поиска:
- •Варианты задания №10
- •Пример выполнения задания №10
- •VIII. Методы многомерной оптимизации
- •2. Необходимое и достаточное условия минимума функции многих переменных:
- •3. Основные методы безусловной многомерной минимизации:
- •Варианты задания №11
- •Примеры выполнения задания №11
- •IX. Обыкновенные диференциальные уравнения. Задача Коши.
- •Пример выполнения задания №12.
§3. Метод Ньютона для системы нелинейных уравнений. Пусть имеется следующая система нелинейных уравнений:
 (6.5)
(6.5)
Как
уже отмечалось выше, для одной переменной
метод Ньютона использует замену искомого
уравнения уравнением прямой или, как
еще говорят, производит линеаризацию
исходного уравнения. Пусть имеется k
- ое приближение:
![]() .
Разложим левые части системы уравнений
в ряд Тейлора и учтем только линейные
члены:
.
Разложим левые части системы уравнений
в ряд Тейлора и учтем только линейные
члены:
 (6.6)
(6.6)
где
![]() ,i=1,2,...,n;
а частные производные вычисляются в
точке k-го
приближения: x1=x1(k),
x2=x2(k),...,xn=xn(k).
,i=1,2,...,n;
а частные производные вычисляются в
точке k-го
приближения: x1=x1(k),
x2=x2(k),...,xn=xn(k).
Заменим в исходной системе нелинейные функции fi(x1,x2,...,xn) на правые части этих приближенных равенств, которые являются линейными функциями относительно переменных xi, i=1,2,...,n. В итоге получим следующую систему линейных уравнений относительно переменных xi, i=1,2,...,n:
 (6.7)
(6.7)
Из
этой системы можно определить значения
xi,
i=1,2,...,n
и вычислить значения k+1-приближения:
![]() .
Данная система уравнений представляют
собой метод Ньютона для системы нелинейных
уравнений.
.
Данная система уравнений представляют
собой метод Ньютона для системы нелинейных
уравнений.
Определитель этой системы называется якобианом.
 . (6.8)
. (6.8)
Для существования решения якобиан должен быть отличен от нуля для каждого шага итерации.
Критерий
окончания.
Итерационный процесс продолжается до
тех пор, пока не выполнятся условия:
![]() ,
для всех i=1,2,...,n.
,
для всех i=1,2,...,n.
Варианты задания №9
С помощью метода Ньютона решить следующую систему уравнений, результаты получить с точностью 0,1.
1. ![]() 2.
2. 
3. ![]() 4.
4. 
5.  6.
6. ![]()
7. ![]() 8.
8. 
9.  10.
10. 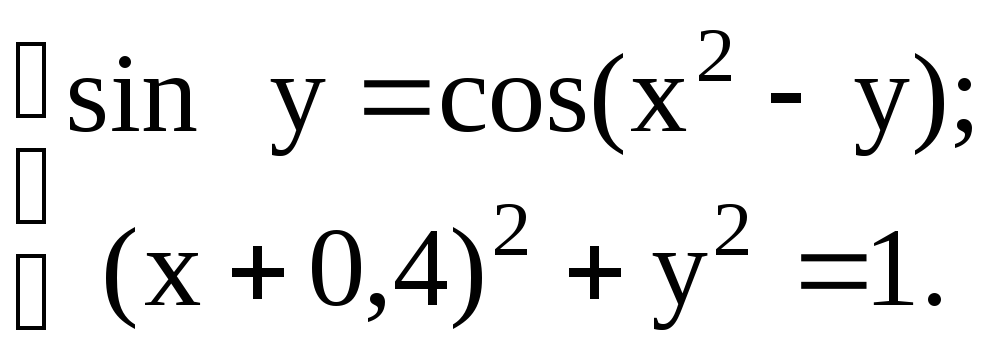
11. ![]() 12.
12. 
13. ![]() 14.
14. ![]()
15. ![]() 16.
16. 
17. ![]() 18.
18. 
19. ![]() 20.
20. 
21. ![]() 22.
22. 
23. ![]() 24.
24. 
25.  26.
26. 
27. ![]() 28.
28. 
29.  30.
30. 
31.  32.
32. 
33.  34.
34. ![]()
35. ![]() 36.
36. 
37.  38.
38. 
39.  40.
40. 
Пример выполнения задания №9
С помощью метода Ньютона решить следующую систему уравнений, результаты получить с точность 0,1.
![]()
1. Согласно метода Ньютона имеем следующую систему уравнений:
![]()
2. Находим частные производные:
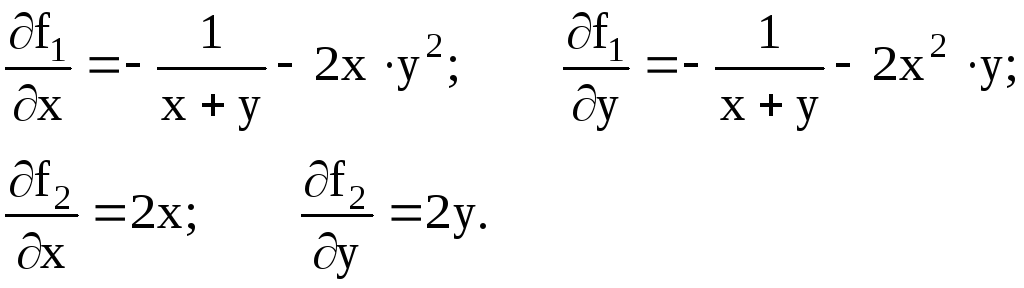
3. Записываем систему уравнений метода Ньютона:

где
![]()
Так как заданная точность равна 0,1, то все вычисления необходимо проводить с точностью как минимум на порядок выше. Поэтому в расчетах будем учитывать два знака после запятой, т.е. расчеты вести с точностью не хуже чем 0,01.
4. Выбираем нулевое приближение: x(0)=1, y(0)=0. Для определения первого приближения имеем следующую систему уравнений относительно x и y:

5. Решая эту систему, получаем: x=0,5; y=-0,5. Находим первое приближение: x(1)=x(0)+x=1,5 и y(1)=y(0)+y=-0,5. Так как x>0,1 и y>0,1; то находим второе приближение, для вычисления которого имеем следующую систему уравнений:

6. Имеем: x=-0,04; y=0,38. Отсюда получаем второе приближение:
x(2)=x(1)+x=1,46 и y(2)=y(1)+y=-0,12. Так как x<0,1 и y>0,1; то записываем систему для третьего приближения:

7. Получаем: x=-0,11 и y=-0,84. Имеем x(3)=x(2)+x=1,35 и y(3)=y(2)+y=-0,96. Так как x>0,1 и y>0,1; то записываем систему для четвертого приближения:

8. Получаем: x=-0,1 и y=0,24. Имеем x(4)=x(3)+x=1,25 и y(4)=y(3)+y=-0,72. Так как x=0,1 и y>0,1; то записываем систему для пятого приближения:

9. Получаем: x=-0,06 и y=0,05. Имеем x(5)=x(4)+x=1,19 и y(5)=y(4)+y=-0,67. Так как x<0,1 и y<0,1; то итерационный процесс прекращаем.
10. После округления имеем приближенное решение: x1,2 и y-0,7.
