ЭМиКМ (пособие)

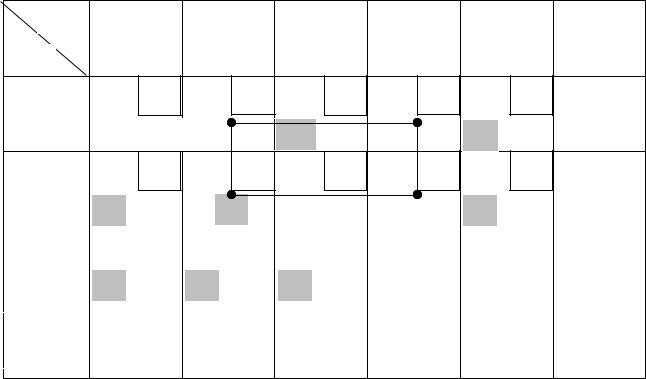
74

Таблица 4.6

Освободим клетку (2, 4), в которой стояло минимальное число, а соответ- ствующую ей переменную x24 исключим из базиса. Получаем новый опорный план ТЗ:

Среди полученных значений симплексных разностей для переменных в свободных клетках имеются положительные числа: 1 в клетках (3, 2) и (3, 3). Это означает, что найденный опорный план не является оптимальным.

Итерация 3. Для каждой занятой клетки таблицы 4.6 (с учетом сделан- ной перестановки) снова рассчитаем значения потенциалов поставщиков и по- требителей:

u1 + v4 = 2;

Полагая u1 = 0, получаем v1 = 2 , v2 = 3, v4 = 2 . Подставляем получен-

Таким образом, имеем следующие значения потенциалов поставщиков и потребителей:

Вычислим симплексные разности для остальных переменных:

Таким образом, имеем следующие значения симплексных разностей:

ij = {−2, − 7, − 5, −1, − 3, − 2,1, 2}. lk = max{ ij} = 33 = 2 ,

xlk = x33 =10.

Подставляем полученные значения в таблицу с опорным планом X2 и

получаем таблицу 4.7.

Пометим заполняемую клетку (3, 3) знаком «+», а затем поочередно клет-

ки (2, 3), (2, 2), (1, 2), (1, 4) и (3, 4) − соответственно знаками «−», «+», «−», «+»

и «−». Среди клеток, образующих цикл и помеченных знаком «−», и вычтем из чисел, стоящих в клетках, помеченных знаком «−».

Таблица 4.7

76

Освободим клетку (1, 2), в которой стояло минимальное число, а соответ- ствующую ей переменную x12 исключим из базиса. Получаем новый опорный план ТЗ:

Среди полученных значений симплексных разностей для переменных в свободных клетках имеются положительные числа: 1 в клетке (3, 2) и 2 в клетке (3, 3). Это означает, что найденный опорный план не является оптимальным.

77

Таблица 4.8

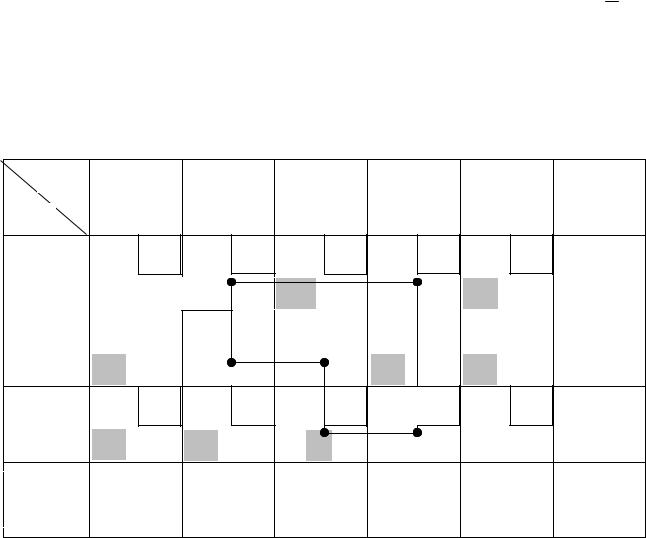
Освободим клетку (2, 4), в которой стояло минимальное число, а соответ- ствующую ей переменную x24 исключим из базиса. Получаем новый опорный план ТЗ:

Z(X4 ) = 2×60 + 2×80 + 4 ×70 +1×60 + 4 ×50 + 3×60 + 2×100 =1200.

Среди полученных значений симплексных разностей для переменных в свободных клетках имеется положительное число: 1 в клетке (2, 4).

79

Таблица 4.9

ПН

ПО

Изменение суммарной стоимости перевозок по мере приближения к оп- тимальному плану показано в таблице 4.10.

Решение ТЗ, имеющих некоторые сложности в постановке

1. В некоторых реальных условиях перевозки груза из определенного пункта отправления Ai в пункт назначения Bj не могут быть осуществлены.

Для определения оптимальных планов таких задач предполагают, что стои- мость перевозки единицы груза из пункта Ai в пункт Bj является сколь угодно

большой величиной M , и при этом условии известными методами находят решение ТЗ. Такой подход к нахождению решения ТЗ называется запрещением перевозок.

2. В отдельных ТЗ дополнительным условием является обеспечение пере- возки по соответствующим маршрутам определенного количества груза. На-

пример, из пункта Ai в пункт Bj требуется обязательно перевести aij единиц

груза. Тогда в соответствующую клетку таблицы, находящуюся на пересечении i -й строки j -го столбца, записывают указанное число aij и в дальнейшем

считают эту клетку свободной со сколь угодно большой стоимостью перевозки

80

M . Для полученной таким образом новой ТЗ находят оптимальный план, ко- торый определяет оптимальный план исходной ТЗ.

3. Иногда требуется найти решение ТЗ, при котором из пункта Ai в пункт Bj должно быть перевезено не менее aij единиц груза. Для определения опти- мального плана такой задачи считают, что запасы Ai и потребности Bj меньше фактических aij единиц. После этого находят оптимальный план новой ТЗ, на

основании которого и определяют решение исходной задачи.

Примечание. При целых ai (i =1, 2,...,m) и bj ( j = 1, 2,...,n) из-за спе-

цифики ограничений ТЗ любое базисное допустимое решение является цело- численным.

81

Глава 5. Задача о назначениях

Задача о назначениях − одна из разновидностей ЗРТ, в которой для вы- полнения каждой работы требуется один и только один ресурс (один работник, один станок, одна автомашина и т. д.). Другими словами, ресурсы не делимы между работами, а работы не делимы между ресурсами. Таким образом, задача о назначениях является частным случаем ТЗ, рассматривающая назначение со- трудников на должности или работы, автомашин на маршруты, водителей на автомашины и т.п.

Экономико-математическая модель задачи о назначениях

Пусть на предприятии (или в подразделении предприятия) имеются n со- трудников S1, S2 , …, Si , …, Sn (i =1,2,...,n), которых необходимо назначить

(распределить) по n работам R1, R2 , …, Rj , …, Rn ( j = 1,2,...,n) . Каждую из

указанных работ может выполнять любой из сотрудников, однако производи- тельность их труда по видам работ различается. В результате проведенных на- блюдений и экспериментов зафиксирована производительность труда сотруд- ников по различным видам работ.

Обозначим aij − производительность i -го сотрудника по j -й работе, а xij − назначение i -го сотрудника на j -ю работу.

82

anj

Из таблицы 5.1 следует, что если сотрудник Si назначен на работу Rj , то xij =1, а остальные элементы этой строки будут равны 0. Таким образом, сумма переменных xij для любой строки или столбца равна 1, т.е. можно запи- сать следующие условия:

i=1 j =1

Таким образом, сущность задачи о назначениях состоит в отыскании та- ких неотрицательных значений xij , чтобы целевая функция (общая производи-

тельность) была максимальной.

Рассмотренная выше задача классифицируется как комбинаторная (пере- борная) задача. Пример решения подобной задачи представлен ниже [17].

Задача. На малом предприятии имеются три работника, которых необхо- димо распределить по трем различным работам. Предварительно определена производительность aij каждого работника по каждой из трех работ (см. табли-

цу ниже).

Представим условие задачи о назначениях в таблице 5.2.