ЭМиКМ (МУ)

УДК 519.8:657.1

Стариков, А.В. Экономико-математическое и компьютерное моделирование [Текст] : метод. указания к выполнению лабораторных работ для студентов специальности 080502 (060800) – Экономика и управление на предприятии (лесной комплекс) / А.В. Стариков, И.С. Кущева ; Федеральное агентство по образованию, Воронеж. гос. лесотехн. акад. – Воронеж, 2006. – 72 с.

Рецензент д–р техн. наук, проф. кафедры информационных и управляющих систем ВГТА В.Ф. Лебедев

4

ВВЕДЕНИЕ

Методические указания предназначены для студентов специальности 080502 (060800) – Экономика и управление на предприятии (лесной комплекс), изучающих дисциплину «Экономико-математическое и компьютерное моделирование». Данные методические указания содержат тексты шести лабораторных работ. Выполнению каждой работы должно предшествовать ознакомление ее с теоретической частью, помещенной, как правило, в начале работы. Студентам надлежит вести рабочую тетрадь, в которой должны отражаться результаты и ход выполнения лабораторных задач, а также основные теоретические выкладки, используемые при этом.

Лабораторная работа №1 рассматривает основные методические

положения по составлению математических моделей и решение задач оптимального планирования производства графическим методом, а также

возможность исследования чувствительности полученного оптимального решения.

Лабораторная работа №2 знакомит студентов с технологией использования табличного процессора Microsoft Excel для нахождения оптимальных решений.

Лабораторная работа №3 рассматривает вопросы нахождения оптимального плана перевозок. В ходе выполнения студенты знакомятся с методикой составления опорного плана перевозок тремя методами: СЗУ, наименьшей стоимости и Фогеля, а затем определением оптимального плана перевозок методом потенциалов. Также рассматривается решение данной задачи с использованием процедуры «Поиск решений» (Solver).

Лабораторная работа №4 знакомит с составлением математической модели и решением задачи о назначениях − частного случая задачи распределительного типа.

Лабораторная работа №5 посвящена вопросам сетевого планирования, в ней описана методика построения сетевого графика, расчета критических путей, временных параметров событий и работ.

Лабораторная работа №6 рассматривает вопросы прогнозирования в экономике и связанные с этим понятия и методы. Студенты на практике овладевают одним из часто используемых методов – линейной регрессией, решив с помощью Microsoft Excel нескольких типовых задач.

5

ЛАБОРАТОРНАЯ РАБОТА №1 (4 часа)

Тема работы: Методика построения экономико-математической модели задачи линейного программирования (ЗЛП). Решение двумерных ЗЛП графическим методом. Анализ и интерпретация результатов решения ЗЛП.

Содержание работы и порядок ее выполнения

Лабораторная работа включает в себя задачу составления оптимального по прибыли плана выпуска двух видов мебельных изделий и рассчитана на 4 часа лабораторных занятий. Условия задач выдаются студентам преподавателем, руководящим выполнением лабораторных работ.

На первом занятии студент занятии знакомится с содержанием работы, а во внеаудиторное время изучает необходимую литературу, составляет по исходным данным математическую модель задачи, выполняет ее решение графическим методом, анализирует полученные результаты, проводит анализ чувствительности решения. По проделанной работе составляется отчет.

Методические указания по составлению и оформлению отчета о лабораторной работе изложены в конце методических указаний.

На втором занятии студент отчитывается по теоретической части лабораторной работы, предоставляет отчет о выполненной работе преподавателю, и защищает полученные результаты.

Методика построения математической модели ЗЛП

Линейное программирование – раздел исследования операций, занимающийся решением таких задач на отыскание экстремальных значений,

для которых классические методы математического анализа оказываются непригодными. К их числу относятся задачи рационального использования сырья и оборудования, составления оптимального плана перевозок, работы транспорта и ряд других, относящихся к области оптимального планирования.

Условие задачи. Предприятию (участку, цеху, отрасли) планируется выпуск n видов продукции (товаров, изделий) Т1,...,Тj‚,...,Тn. Для выпуска этих видов продукции необходимо использовать m видов ресурсов (сырья, оборудования и др.). В начале планового периода эти ресурсы выделены предприятию в количествах b1,...,bi,...,bm соответственно. На производство одного изделия Тj расходуется aij ресурсов i–го вида. От реализации одного изделия Тj предприятие получает прибыль pj=cj–sj, где cj – отпускная оптовая цена изделия Тj, а sj – себестоимость. Найти такой план выпуска продукции, чтобы суммарная прибыль от реализации продукции была наибольшей.

Для составления математической модели этой задачи неизвестные количества изделий каждого j–го вида обозначаются через хj, j=1,2,...,n. Тогда

6

цель задачи – условие получения максимальной суммарной прибыли – можно записать следующим образом:

n

Z = p1x1 +K+ p j x j +K+ pn xn = å p j x j ® max. (1.1)

j=1

Из (1.1) видно, что суммарная прибыль линейно зависит от искомых объемов производства различных видов продукции. Величину Z называют целевой функцией (критерием эффективности) задачи.

Анализ целевой функции (ЦФ) показывает, что увеличение Z имеет место при увеличении любого из хj, однако такое увеличение возможно лишь в пределах, ограниченных выделенными на производство (ограниченными) ресурсами. Поэтому элементы искомого решения xj нельзя выбирать произвольно: суммарное количество i–го ресурса, затраченное на производство всех n видов продукции, не должно превышать имеющегося количества bi этого ресурса. Таким образом, можно записать следующую систему неравенств:

Наконец, определяемый объем производства не может быть отрицательным (продукция или производится, тогда xj>0, или не производится, тогда хj=0). Следовательно, систему неравенств (1.2), носящую название системы ограничений, следует дополнить следующими ограничениями, называемыми естественными или тривиальными:

7

где символ называется квантором общности и заменяет слова «для всех». Аналогично систему ограничений (1.3) можно представить в виде

Соотношения (1.1), (1.2), и (1.3) представляют математическую модель

задачи поиска оптимального по прибыли плана выпуска продукции из имеющихся ресурсов, или задачи оптимального использования ресурсов. При этом неравенства (1.2) и (1.3) составляют систему ограничений, а выражение (1.1) – целевая функция, служащая для оценки качества решения, –

формализует критерий эффективности.

Врассмотренной формализованной постановке задача поиска оптимального по прибыли плана использования ресурсов формулируется так:

найти вектор, т.е. упорядоченный набор неотрицательных значений xj, удовлетворяющий системе ограничений (1.2) и обеспечивающий максимальное значение линейной функции Z (1.1).

Втом случае, когда ЗЛП содержит всего две неизвестные величины x1 и x2, может использоваться простой и наглядный графический метод.

Если среди ограничений (1.2) встречаются как уравнения (равенства), так

инеравенства, задача линейного программирования называется общей. Если же среди ограничений (1.2) имеются только неравенства, задача линейного программирования называется стандартной. Задачу линейного программирования называют канонической, если система ограничений (1.2) содержит только уравнения.

Упорядоченный набор чисел α1,α2,...,αn называется решением системы, содержащей n неизвестных, если в результате подстановки этих чисел на место соответствующих неизвестных х1,х2,...,xn каждое уравнение системы обращается в тождественное равенство.

Если система уравнений имеет хотя бы одно решение, она называется совместной; она называется несовместной, если не имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение, если более одного решения – неопределенной. Именно с такими

системами уравнений приходится иметь дело в задачах оптимального планирования.

Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если они обе несовместны или обе имеют одни и те же решения.

В процессе решения систем линейных уравнений над системой разрешается проводить преобразования, переводящие ее в эквивалентную исходной. Во-первых, обе части любого уравнения системы можно умножать на одно и то же число, не равное нулю; во-вторых, к обеим частям любого

уравнения системы можно прибавлять соответствующие части другого уравнения системы, предварительно умноженные на произвольное число.

Допустимые значения х1 и х2 ограничены располагаемыми объемами ресурсов. Обивочная ткань используется только на производство кроватей, причем, на каждую кровать требуется 3,3 м2 ткани. Следовательно, ограничение

по ткани надо записать так

3,3x2 ≤ 396. (1.7)

То есть общее количество обивочной ткани, необходимое на производство х2 кроватей, не должно превышать имеющегося – 396 м2.

(количество пиломатериалов, затрачиваемых на производство х1 шкафов и х2 кроватей, не должно превышать имеющихся 14,4 м3),

5x1 + 4x2 £ 810 (1.9)

(количество станко-смен оборудования, необходимое на производство х1 шкафов и х2 кроватей, не должно превышать их ресурса, равного 810 станко– сменам),

(количество плитных материалов, нужное для производства х1 шкафов, не должно превышать выделенных для производства 325 м2. По условиям задачи плита не используется на производство кроватей и, следовательно, (1.10) не зависит от х2).

Каждый из рассматриваемых видов мебели может производиться в определенных количествах или не производиться вовсе. Следовательно, можно

записать

Итак, математическая модель задачи поиска оптимального по прибыли

плана выпуска двух видов мебели в виде модели линейного программирования составлена. Это соотношения (1.6) – (1.11). Задачу теперь можно сформулиро- вать так: найти такие неотрицательные значения переменных х1 и х2, которые удовлетворяют линейным ограничениям – неравенствам (1.7) – (1.11) и обеспечивают максимальное значение ЦФ (1.6).

Задание 1. По условию задачи, выданному преподавателем, составить экономико-математическую модель задачи поиска оптимального плана выпуска двух видов мебельных изделий.

Решение ЗЛП графическим методом

10

Ограничения задачи – неравенства (1.2) – (1.3) можно представить как выпуклый многогранник в n-мерном пространстве (симплекс). Здесь n – число переменных. Этот многогранник ограничивает область допустимых значений переменных. Если n=2, как в рассматриваемом случае, симплекс вырождается в

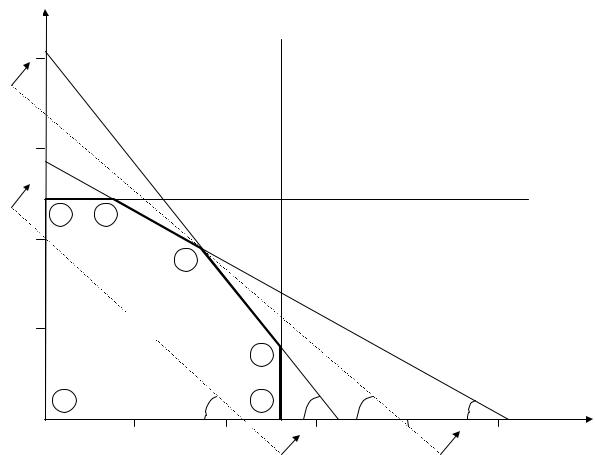
выпуклый многоугольник и его легко построить на плоскости в прямоугольных координатах, как показано на рисунке 1.1.

Для построения симплекса необходимо построить все прямые, соответствующие системе ограничений (1.7) – (1.11). По оси абсцисс откладываются величины х1, а по оси ординат – х2 . Ограничение х1³0 означает, что область допустимых решений расположена правее оси ординат. Аналогично, ограничение х2³0 означает, что точки плоскости, соответствующие допустимым решениям системы ограничений, должны лежать на плоскости выше оси абсцисс. Ограничение (1.7) соответствует прямой, параллельной оси абсцисс и проходящей через точку на оси ординат х2=396/3,3=120.

Рис. 1.1

Прямые, соответствующие ограничениям (1.8) и (1.9) строятся по точкам, лежащим на осях координат. Так, полагая в (1.8) x1=0, находится точка,

лежащая на оси ординат: x2(0) =14,4/0,1=144; аналогично находится точка на оси