ЭМиКМ (пособие)

46

ваний. Обозначим через x1 количество плит, раскраиваемых по первому вари- анту, x2 − по второму варианту, x3 − по третьему варианту. Составим ограни- чение по выпуску заготовок 1-го типоразмера. Из одной плиты по первому ва- рианту раскроя получаются две таких заготовки, из x1 плит 2x1 заготовок 1-го типоразмера. Кроме того, по одной такой заготовке получится при раскрое ка- ждой плиты по второму варианту. Всего по этому варианту раскраивается x2 плит, из которых вырабатывается x2 заготовок 1-го типоразмера. Таким обра- зом, общее количество заготовок 1-го типоразмера равно 2x1 + x2 и по усло- вию задачи оно не должно быть менее 300, т.е. имеем следующее ограничение:

2x1 + x2 ³ 300.

Аналогичным образом составляется ограничение по выработке заготовок 2-го типоразмера

x1 + 2x2 + 3x3 ³ 400.

Выражение для суммарного количества отходов при раскрое является це- левой функцией, имеющей вид:

Z(X ) =18850x1 +18450x2 +18050x3 .

Наконец, следует учесть естественные ограничения на неотрицательность

переменных

x1 ³ 0, x2 ³ 0, x3 ³ 0.

Таким образом, экономико-математическая модель задачи оптимального раскроя ДСтП на заготовки имеет вид: найти такой план раскроя

X = (x1, x2 , x3 ), при котором целевая функция, определяющая суммарную площадь отходов, минимальна

Z(X ) =18850x1 +18450x2 +18050x3 ® min

и выполняются следующие ограничения:

ì2x1 + x2 ³ 300,

ïíx1 + 2x2 + 3x3 ³ 400, ïîx1 ³ 0, x2 ³ 0, x3 ³ 0.

Задача №10. Определить оптимальный план раскроя 100 листов фанеры размером 2,5×1,5 м на прямоугольные заготовки размерами 2×1 м, 1×0,75 м и 0,5×0,5 м в ассортименте 1:4:12.

47

Общая постановка задачи о раскрое одного материала

На раскрой (распил, обработку) поступает материал одного образца в ко- личестве a единиц. Требуется изготовить из него l разных комплектующих изделий в количествах, пропорциональных b1,b2 ,...,bl (условие комплектно- сти). Каждая единица материала может быть раскроена n различными спосо- бами, причем использование i -го способа (i =1, 2,...,n) дает aik единиц k -го изделия (k = 1, 2,...,l).

Необходимо найти план раскроя, обеспечивающий максимальное число комплектов.

Составим экономико-математическую модель задачи. Обозначим xi −

число единиц материала, раскраиваемых i -м способом, и x − число изготавли- ваемых комплектов изделий.

Так как общее количество материала равно сумме его единиц, раскраи- ваемых различными способами, то

X = (x1, x2 ,..., xn ), удовлетворяющее системе уравнений (2.18) и (2.19) и ус-

ловию (2.20), при котором функция Z(X ) = x принимает максимальное значение.

Общая постановка задачи о раскрое нескольких материалов

Задачу о раскрое можно легко обобщить на случай m раскраиваемых ма-

48

(i =1, 2,...,n) дает aijk единиц k -го изделия (k = 1, 2,...,l), а запас j -го мате- риала равен a j единиц.

Обозначим xij − число единиц j -го материала, раскраиваемого i -м спо-

собом. Экономико-математическая модель задачи о раскрое в общей постанов-

ке примет вид: найти такое решение X = (x11, x12,..., xnm ), удовлетворяю-

щее системе

<Здесь должна быть задача о раскрое нескольких материалов. Например, про- изводственный участок мебельного цеха изготавливает столярные ящики, на которые расходуются доски (для каркаса), ДСтП (для передней стенки) и ДВП (для дна). Придумать!!! >

47

Глава 3. Способы решения задачи линейного программирования

В данной главе на примере решения простой задачи производственного планирования рассмотрены следующие два способа решения ЗЛП: графический и симплекс-метод.

Экономико-математическая модель задачи производственного планирования

( j = 1, 2,...,n), причем известно количество i -го вида ресурсов, затрачиваемое на выпуск единицы j -го вида продукции, которое обозначим через aij . Кроме того, известна прибыль от реализации единицы каждого из j видов выпущен- ной продукции, которую обозначим через c j .

С учетом введенных обозначений экономико-математическая модель за- дачи формирования производственного плана, обеспечивающего получение максимальной прибыли, может быть представлена следующим образом: найти

при которых целевая функция задачи (прибыль от реализации произведенной продукции) принимает максимальное значение

Как отмечалось выше, данная задача относится к ЗЛП, поскольку и целе- вая функция, и ограничения являются линейными.

Выражения (3.1) и (3.2) можно записать в краткой форме:

48

n

Z(X ) = åc j x j ® max . (3.5)

j=1

Другим кратким способом записи выражений (3.1) и (3.2) является мат- ричная форма [9]:

X = (x1 x2 ... xn ) , т.е. число, равное сумме произведений соответствующих

состоят соответственно из коэффициентов при переменных и свободных чле- нов.

Пример построения экономико-математической модели задачи производственного планирования

49

Задача №10. Предприятие производит два вида продукции P1 и P2 , используя для этого три вида сырья: S1, S2 , S3. Нормы расхода сырья каждого

вида приведены в таблице 3.1. Найти такой план выпуска продукции, при кото- ром прибыль от ее реализации является максимальной.

Экономико-математическую модель данной задачи можно записать сле- дующим образом: определить объемы производства продукции P1 и P2 , при

которых достигается максимизация целевой функции

где x1 и x2 − количество единиц продукции P1 и P2 .

Так как в математической модели задачи использованы только две пере- менные x1 и x2 , ее можно решить графически.

Графический способ решения ЗЛП

Графический (геометрический) способ решения ЗЛП обычно предполага- ет выполнение следующих действий:

1.Запись математических выражений, представляющих целевую функ- цию и ограничения, в виде равенств (уравнений).

2.Построение на графике прямых для уравнений, соответствующих огра- ничениям.

3.Определение области допустимых решений (ОДР) для задачи.

4.Построение на графике прямой, соответствующей целевой функции.

50

5.Параллельный перенос (перемещение) прямой, построенной для целе- вой функции, в одну из крайних точек ОДР для получения оптимально- го решения.

Пример решения задачи производственного планирования графическим методом

Решим задачу производственного планирования, рассмотренную выше, графическим способом. Вначале определим ОДР, в которой одновременно вы- полняются все ограничения, представленные в модели задачи. Для этого пред- ставим каждое из ограничений (3.13)−(3.17) в виде равенства (уравнения) и по- лучим для них по паре точек, через которые проведем на графике отрезки пря- мых.

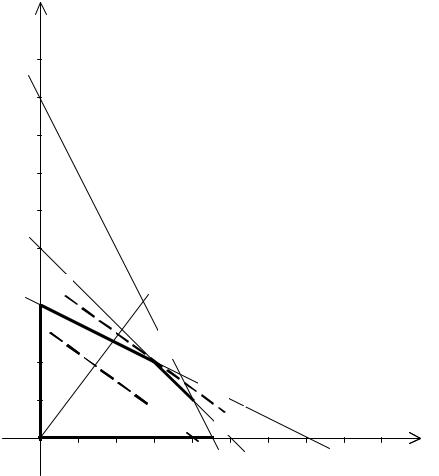
Таким образом, ОДР задачи представляет собой выпуклый пятиугольник ABCDE, показанный на рисунке 6.

В качестве уравнения для целевой функции можно использовать выраже- ние 3x1 + 4x2 =12, правая часть которого равняется произведению коэффици- ентов при неизвестных. Полагая x1 = 0, получим x2 = 3. Аналогично, при x2 = 0, получим x1 = 4 . Следовательно, прямая для целевой функции прохо-

дит через пару точек с координатами (0; 3) и (4; 0). На рисунке эта прямая обо- значена пунктиром.

52

Анализ чувствительности модели задачи производственного планирования

После того, как найдено оптимальное решение задачи производственного планирования, можно выполнить анализ его чувствительности к изменениям исходных данных модели. В частности, целесообразно выяснить следующее

[16]:

1.На сколько можно увеличить запас некоторого вида сырья для улучше- ния полученного оптимального плана?

2.На сколько можно снизить запас некоторого вида сырья при сохране- нии полученного оптимального плана?

3.Увеличение запасов какого вида сырья наиболее выгодно?

4.Каков диапазон изменения того или иного коэффициента целевой

функции, при котором не происходит изменение оптимального реше- ния?

Прежде всего, выполним классификацию ограничений, разделив их на

активные (или связывающие), и неактивные (или несвязывающие). Активные ограничения соответствуют прямым, проходящим через точку, представляю- щую оптимальное решение (на рисунке 7 это вершина C пятиугольника ABCDE). Неактивные ограничения соответствуют прямым, которые ограничивают ОДР, но не проходят через точку оптимального решения.

В данном случае активными ограничениями являются (1) и (3), поскольку соответствующие им прямые проходят через точку, координаты которой и дают оптимальный производственный план. Активные ограничения лимитируют за-

пасы сырья S1 и S3, которые логично отнести к разряду дефицитных, тогда

как неактивное ограничение (2) ассоциируется с видом сырья S2 , запас которо- го имеется в некотором избытке, т.е. оно является недефицитным.

Вначале рассмотрим влияние увеличения запасов сырья S1 (ограничение

1) на улучшение полученного оптимального плана. Из рисунка видно, что при увеличении запаса этого вида сырья соответствующая прямая (в частности, от- резок СD) перемещается вверх параллельно самой себе, постепенно стягивая в точку треугольник CKD. В точке K, соответствующей оптимальному решению, активными являются ограничения (2) и (3), а ограничение (1) становится неак-

тивным. Поэтому запас сырья S1 не следует увеличивать сверх того предела,

когда ограничение становится неактивным. Это предельное значение рассчиты- вается путем подстановки координат точки K(11/3; 5/3) в левую часть ограни- чения (1):

1×113 +1× 53 = 163 ,

Z(K) = 3×113 + 4 × 53 = 533 .

Аналогично рассматривается вопрос о целесообразности увеличения де- фицитного сырья S3. Из рисунка видно, что при увеличении этого вида сырья

соответствующая прямая (в частности отрезок BC), перемещается вверх парал- лельно самой себе. В точке L ограничение (3) становится неактивным, поэтому

объем сырья S3 не следует увеличивать сверх этого предела. Это предельное

значение рассчитывается путем подстановки координат точки L(0; 5) в левую часть ограничения (3):

1×0 + 2 ×5 =10,

Z (L) = 3×0 + 4 ×5 = 20 .

Таким образом, предельные запасы для сырья S1 и S3 составляют соот-

ветственно 5 13 и 10 единиц соответственно. Дальнейшее повышение этих за-

пасов нецелесообразно, поскольку не приведет к улучшению оптимального ре- шения задачи.

Рассмотрим теперь вопрос об уменьшении запаса недефицитного сырья S2 (ограничение 2). Из рисунка видно, что, не изменяя оптимального решения,

соответствующую прямую (в частности, отрезок KE), можно перемещать па- раллельно самой себе до пересечения с точкой C. Уменьшение запасов сырья