30

Оглавление

РАЗДЕЛ 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ КРИПТОГРАФИИ 5

РАЗДЕЛ 2. КРИПТОГРАФИЧЕСКИЕ СИСТЕМЫ С ОТКРЫТЫМ КЛЮЧОМ 15

РАЗДЕЛ 3. Контрольные задания 22

Библиографический список 30

Предисловие

Теория чисел, наряду с геометрией, является одной из древнейших областей математики. Значительный вклад в эту область знаний внесли виднейшие математики древности и нового времени: Евклид, Пифагор, П. Ферма, Эйлер и др. Однако до последнего времени теория чисел считалась одной из наиболее абстрактных областей математики, не имеющей практического применения.

Подобные взгляды господствовали в математике до становления теоретической криптологии в последней четверти XX в. Разработка криптографических систем с открытым ключом обусловила новые области применения теории чисел. Теория чисел из абстрактной научной дисциплины, занимающейся коллекционированием фактов о замечательных свойствах натуральных чисел, превратилась в инструмент синтеза и анализа криптографических систем, чрезвычайно востребованных на практике [7].

Подобное положение дел привлекло к теории чисел повышенный интерес как научных кругов, так и широкой общественности. Обсуждение теоретических вопросов широко освещается в околонаучной прессе. Для решения сугубо научных задач (факторизация больших чисел, поиск простых чисел Ферма и Мерсенна и т.д.) спонтанно организуются массовые сообщества добровольцев.

Подобный всплеск интереса к теории чисел подтверждает актуальность решаемых ею задач и их важность для развития сферы информационных технологий.

Раздел 1. Математические основы криптографии

1.1. Делимость и алгоритм евклида

1.1.1 Отношение делимости

Понятие делимости является одним из фундаментальных понятий теории чисел.

Определение 1. Для данных целых чисел иговорят, чтоделит(или иными словами, чтоделится на), и обозначаютесли существует такое целое число, что:

, где множество целых чисел.

(1)

В этом случае число называют делителем числа. Очевидно, что любое целое числоимеет, по крайней мере, два положительных делителя: 1 и.

Определение 2. Собственным делителем числа называют любой положительный делитель, не равный.

Определение 3. Нетривиальным делителем числа называют любой положительный делитель, не равный 1 или.

Введенное понятие нетривиального делителя используем для определения понятия простого числа.

Определение 4. Простым (prime) называют целое число большее 1, не имеющее нетривиальных делителей.

Определение 5. Составным (complex) называют число, имеющее, по крайней мере, один нетривиальный делитель.

Непосредственно из определения делимости (1) следуют свойства делимости:

1. Если делит, и− любое целое число, тоделит произведение:

.

2. Если делит, а, в свою очередь, делит, тоделит:

.

3. Если делит, иделит, тоделит:

.

В дальнейшем, для некоторого простого и целого, неотрицательного числазапись видабудем использовать для обозначения того факта, что− наивысшая степень, делящая:

.

В этом случае говорят, что точно делит.

Основная теорема арифметики утверждает, что любое натуральное число может быть представлено в виде произведения простых делителей единственным образом, с точностью до перестановки. Данное представление принято записывать в форме произведения делителей в соответствующих степенях, располагая простые числа в порядке возрастания.

Пример 1. Рассмотрим разложение числа в виде делителей в соответствующей степени:

.

Из основной теоремы арифметики следуют свойства отношение делимости:

4. Простое число делит произведение целых чисел, в том и только в том случае, когдаделит, либоделит:

.

5. Если делитиделит, и еслиине имеют общих делителей больших 1, то произведениеделит:

.

Из основной теоремы арифметики следует также простой способ отыскания всех делителей по его разложению. А именно, любой делительчисладолжен быть произведением тех же простых сомножителей в степенях, не превышающих степени, точно делящих.

Таким образом, если , тодля

Пример 2. Для нахождения делителей числа необходимо взятьв степениили, умножить нав степениили, нав степениилии нав степениили.

В этих условиях число всех делителей есть произведение числа способов выбора степени для каждого простого делителя, которое, в свою очередь, равно . Иначе говоря, числоимеет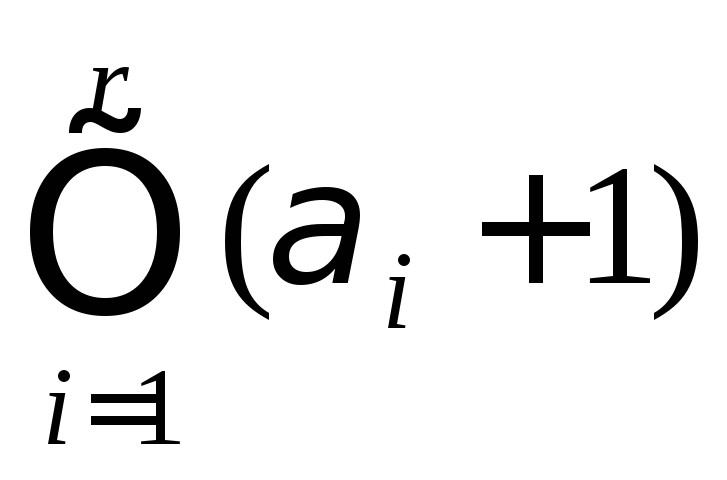различных делителей [8,9].

Пример 3. Число имеетразличных делителей.

Определение 6. Наибольшим общим делителем двух данных чисел и(обозначается), не равных одновременно нулю, называется наибольшее целое число, делящее одновременнои.

Нетрудно показать, что приведенное выше определение эквивалентно следующему.

Определение 7. − есть единственное целое положительное число, которое делит и, и делится при этом на любой их общий делитель.

Из школьного курса математики известен следующий способ нахождения наибольшего общего делителя двух положительных чисел по известному разложению на множители. Для отыскания необходимо взять все простые числа, входящие в оба разложения, и каждое возвести в степень, равную минимуму из двух соответствующих показателей.

Пример 4. Пусть дано и. Тогда.

Определение 8. Наименьшим общим кратным двух данных чисел и(обозначается), не равных одновременно нулю, называется наименьшее целое положительное число, делящееся одновременно наи.

Имея разложение на простые множители чисел и, можно получить значение, взяв все простые числа, входящие хотя бы в одно из разложений, и каждое возвести в степень, равную максимальной из имеющихся в двух разложениях.

Кроме того, нетрудно показать, что наибольший общий делитель и наименьшее общее кратное связаны следующим соотношением:

.
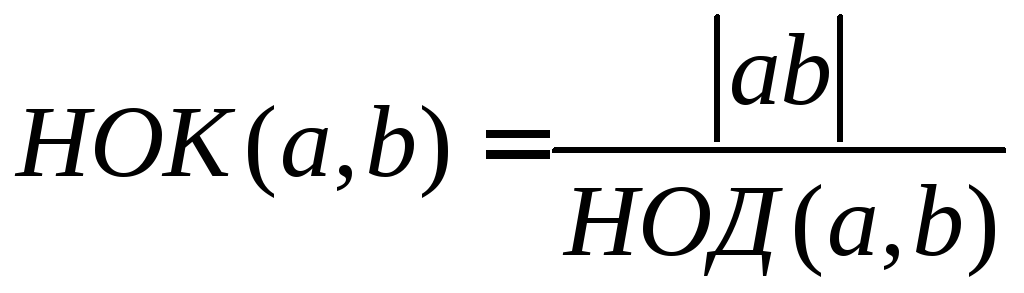