
- •2.6 Стробирование и селекция отметок целей при обработке информации о воздушной обстановке
- •Алгоритмы селекции отметок в стробах.
- •Метод минимальных эллиптических отклонений.
- •3Нание σ*доп позволяет ограничить пределы строба и в дальнейшем сформулировать условие попадания селектируемых отметок Хиj Уиj в площадь оптимального строба.
Метод минимальных эллиптических отклонений.
Данный метод является одним из общих методов селекции траекторий целей, позволявшим учитывать влияние на качество ВОИ таких факторов, как вид совершаемого целью маневра, наличие пропусков отметок в зоне наблюдения в предшествующих циклах наблюдения, ошибки съема координат целей. Селекция отметок осуществляется в стробе эллиптической формы, координаты центра и размеры которого определяются по результатам обработки информации в n предыдущих циклах работы источника информации (обзорах РЛС). Процесс отбора отметки, принадлежащей сопровождаемой цели, разделяется на несколько последовательно выполняемых операций (блок-схема алгоритма стробирования и селекции отметок в стробе методом минимальных эллиптических отклонений представлена на рис. (2.22).
Определение размеров и формирование оптимального строба (блоки 1, 2, 3).
После поступления на вход алгоритма селекции измеренных значений координат отметки Хиj, Уиj, полученных в k-м обзоре РЛС, учета дополнительных данных определяются средние квадратические отклонения координат j-й сопровождаемой цели, δ Δx, δ Δy от центр строба.
По полученным значениям δ Δx, δ Δy, при известных величинах средней плотности ложных отметок μ и порогового значения φ определяются размеры "оптимального" строба, то есть строба, значений которого в процессе селекции гарантирует выполнение требований о том, чтобы значение вероятности принятия о принадлежности ложной отметки к сопровождаемой траектории не превышало заданного уровня. Размеры оптимального строба характеризуются (рис.2.21) величиной полуосей
a=σ*доп δ Δxj и b= σ*доп δ Δyj,
где σ*доп -допустимое значение суммарного эллиптического отклонения.
3Нание σ*доп позволяет ограничить пределы строба и в дальнейшем сформулировать условие попадания селектируемых отметок Хиj Уиj в площадь оптимального строба.
Напомним, что значение σ*доп определяет и величину вероятности попаданий отметки в эллипс рассеивания
P[(Xj, Yj)S],
р
Рис.
2.22. Алгоритм селекции отметок целей
методом минимальных эллиптических
отклонений.
![]() (2.32).
(2.32).
В таб. 2.3 приведены некоторые наиболее часто используемые на практике величины функции (2.32) и соответствующими им значения σ*доп .
Величина σ*доп находиться их выражения (2.32) в предположении что заданный уровень вероятности правильной селекции достигается уже при равенстве отношения правдоподобия Wц(ΔXj,ΔYj)/Wμ(ΔXj,ΔYj) порогового значения φ, то есть из равенства
![]() (2.33)
(2.33)
Таблица 2.2
Допустимые значения суммарного эллиптического отклонения
|
Р[(X,Y)ЄS] |
σ*доп . |
R доп. |
|
0,50 |
1,117 |
1,17 σ Δ |
|
0,60 |
1,354 |
1,35 σ Δ |
|
0,70 |
1,552 |
1,55 σ Δ |
|
0,75 |
1,668 |
1,67 σ Δ |
|
0,80 |
1,794 |
1,79 σ Δ |
|
0,85 |
1,948 |
1,95 σ Δ |
|
0,90 |
2,146 |
2,15 σ Δ |
|
0,95 |
2,448 |
2,45 σ Δ |
|
0,99 |
3,035 |
3,04 σ Δ |
|
0,999 |
3,717 |
3,72 σ Δ |
Расчетная формула для определения *доп выводится из выражения (2.33). После логарифмирования и ряда очевидных преобразований она имеет вид:
*2допj =-2ln2xjyj. (2.34)
Найденные значения σΔх, σΔу и *доп позволяют построить оптимальный строб Хэт, Yэт вычисляются для каждого k-го цикла обработки информации в соответствии с принятым алгоритмом сглаживания и экстраполяции (блок 11).
Стробирование отметок (блоки 4, 5, 6). Отбор отметок попадающих площадь оптимального строба, проводится путем сравнений эклиптических отклонений j-й отметки *j2 и с допустимым значением *допj. В целях сокращения объема вычислений при стробировании сравниваются квадраты отклонений, то есть *j2 и *допj2.Каждая j-я отметка считается попавшей в площадь строба, если выполняется условие *j2 *допj2. Тогда правило стробирования отметок может быть записано в виде:
(Xj,Yj)S, если *j2 *допj2,
(2.35)
(Xj,Yj)S, если *j2 *допj2.
Значение *j2 определяется предварительно по формуле (2.31) учетом соотношений:
Xj-Xиj+Xэтj;
Yj-Yиj+Yэтj;
Все N отметок, для которых справедливо условие (2.35), фиксируются и из их числа в дальнейшем выбирается единственная отметка, имеющая наибольшую вероятность принадлежности к сопровождаемой трассе.
Селекция опечаток в стробе (блоки 7, 8, 9, 10). Дальнейший ход процесса селекции зависит от числа отметок М, зарегистрированных в пределах оптимального строба при выполнении операции стробирования.
Если в строб попадает одна отметка (N -1), то она принимается за продолжение сопровождаемой трассы и ее координаты Хиj, Yиj поступают в алгоритм экстраполяции в качестве действительных значений координат вершины траектории.
При отсутствии отметок в стробе (N - О), а это может иметь место, например, при пропуске j-й цели в k-м обзоре, за продолжение траектории принимается центр строба, то есть полагаются, что Xтj-Xэт и Yтj - Yэт. Но если при сопровождении цели такая ситуация (N-0) повторяется несколько раз подряд, то очевидно, такую цель сопровождать нецелесообразно. Условие сброса цели с сопровождения или необходимости продолжать ее обработку выбирается основе критерия вида l/lдоп, где 1- количество следующих подряд обзоров РЛС, в которых наблюдается отсутствие отметки Хиj, Yиj в пределах строба; 1доп - допустимое (пороговое) значение l.
Решение о сбросе о или продолжении сопровождения 1 j-й цели и принимается по правилу:

При попадании в площадь строба нескольких отметок (N>1) вступает в силу оптимальное правило селекция методом минимальных эллиптических отклонений. Сущность оптимального правила состоит в выборе из числа m попавших в строб отметок той отметки, суммарное эллиптическое отклонения которой от центра строба минимально.
В соответствии с этим правилом к сопровождаемой траектории относиться r-я отметка, имеющая δ*г -[δ*j]min; j-1,m. Координаты этой отметки Хиг, Yиг принимаются за вершину трассы и выдаются в алгоритм экстраполяции.
Оптимальное правило селекции целей методом минимальных эллиптических отклонения базируется на критерии максимального правдоподобия. В соответствии с этим критерием к сопровождаемой траектории следует относить ту отметку, для которой значения функции правдоподобия L(ΔХ, ΔУ) максимально. А это-условие выполняется, как было показано ранее, при минимальном значении эллиптического отклонения.
Главное достоинство минимальных .эллиптических отклонений состоит в том, что используемая при селекции эллиптическая форма строба достаточно корректно отражает реальный характер рассеивания отметок целей относительно экстраполированной траектории учитывать ряд факторов, оказывающих определяющее влияние на величины отклонений отметок от центра строба. Однако практическая реализация алгоритма селекции этим методом связана с необходимостью выполнения большого объема вычислений, что приводит к ужесточению требований производительности ЭВМ АСУ.
Метод минимальных отклонений. В тех случаях, когда средние квадратические отклонения Δх и Δу примерно одинаковы, эллиптическое распределение может быть заменено круговым (замена допустима, если отношение большего СКО к меньшему не превосходит 1.5... 1,6). Это позволяет упростить алгоритм стробирования и селекции отметок. Действительно, если Δх = Δу = Δ , эллипс рассеивания (2.31) превращается в окружность;
![]()
(2,36)
![]()
Радиус R, окружности определяет линейное отклонение отметки Аj от центра строба ЭТ (рис, 2.23). Чем меньше расстояние Rj, тем больше значение плотности распределения Wц(ΔX,ΔY) и, следовательно, выше вероятность принадлежности отметки к сопровождаемой цели. Поэтому при попадании в круговой строб нескольких отметок (N>1) правило селекции цели сводится к отыскано (отметки Аr, лежащей ближе других к центру строба, то есть отметки, которой соответствует минимальное линейное (круговое) отклонение
Rr = min[Rj], j-1, m. (2.37)
В условиях, когда в стробе оказывается не более одной отметки, за продолжение трассы принимается либо центр строба (при N=0) , либо единственная находящаяся в площади строба отметка (при N=1) Следовательно, правила выбора продолжения траектории для обоих рассмотренных методов в подобных ситуациях полностью совпадают (блоки 7 и 9 на рис. 2.).
Размер оптимального строба Rдоп. в пределах которого осуществляется отбор отметок из выражения (2.34) с учетом соотношений
xj=yj=j и допj=Rj/xj;
(2.38)
Rдопj2=-2jln2j.
Кроме того, величина Rдоп может быть выбрана априорно, исходя из условия обеспечения требуемого значения вероятности попадания j-й отметки в круговой строб,
 (2.39)
(2.39)
При известном среднем квадратическом отклонении величина Rдоп находится по табл.2.3. Однако при этом подходе к выбору Rдоп необходимо помнить, что увеличение размеров строба ведет и к росту вероятности попадания в его площадь ложных отметок.
Метод минимальных линейных отклонений даже при правильном выборе Rдоп обеспечивает высокую точность сопровождения целей только в случае равенства величин СКО Δх и Δу, а это равенство далеко не всегда соблюдается на практике.
Вместе с тем данный метод удобен для реализации в АСУ, где селекция отметок в стробе и съем координат выбранной отметки осуществляется оператором, так как отметка, лежащая ближе других к центру строба, достаточно уверенно обнаруживается визуально.
Метод одного строба. Использование при ВОИ рассмотренных выше точных методов селекции и стробирования вызывает необходимость формировать при сопровождении нескольких целей множество перестраиваемых по размерам эллиптических или круговых стробов (блоки 1, 2, 3 на рис. 2.22). Это объясняется тем, что суммарные ошибки измерения к экстраполяции координат Δхj и Δуj, для каждой цели различны в силу индивидуальности характера их движения, неравнозначности условий, в которых осуществляется обнаружение целей и съем координат. А от значений Δхj и Δуj при прочих равных условиях зависят размеры стробов *доп и Rдоп. В связи с этим практическая реализация точных методов возможна только при наличии на пункте управления ЦВМ достаточно высокой производительности.
В тех случаях, когда возможности вычислительных средств АСУ ограничены, при селекции траекторий используется метод одного строба. Основная особенность метода состоит в том, что стробирование разных целей осуществляется с помощью одного и того же строба.
Р
Рис.
2.23. Круговой строб.
О
Рис.
2.24. Равновеликие стробы.
При переходе от эклиптических к прямоугольным стробам идя сохранения в процесс сопровождения целей требуемого значения вероятности попадания реальных отметок в площадь строба Р[(Х, Y)S] оптимальный эллиптический строб ваменяется равновеликим прямоугольным. Центр такого строба совпадает с экстраполированной, точкой ЭТ, а стороны параллельны главным осям рассеивания (рис.2.24).
Размеры прямоугольного строба Хс, Yс определяются из условия равенства площадей эллипса S1 и прямоугольника S2:
S1=ab-S2-4XcYc. (2.40)
Однако из условия нельзя получить однозначного решения задачи и выбора размера строба. Поэтому на величину одной из сторон рав-новеликого прямоугольника, например, 2Xc, обычно накладывается следующее ограничение:
2Xc=a![]() .
.
тогда в соответствии с выражением (2.40):
Xc
=0,5 a![]() -0,89a-0,89*допx;
-0,89a-0,89*допx;
(2.41)
Yc
=0,5 b![]() -0,89b-0,89*допy.
-0,89b-0,89*допy.
П
 Рис.
2.25. График функции P=f(*доп).
Рис.
2.25. График функции P=f(*доп).
![]() .
.
Стороны равновеликого прямоугольного строба могут быть выбраны и более простым способом. Предположим, что в качестве Хс выбрана длина большей полуоси эллипса а. Тогда из равенства (2.40) находим Yс = /4b - 0,785b. Дополнительная относительная погрешность в величине Р[(Х, Y)S] при этом возрастает до 2,5% (кривая 2 на рис. 2.25).
Аналогичным образом осуществляется переход от оптимального кругового строба к равновеликом-/ квадратному (рис. 2.24).
Размеры квадратного строба Хс-Yс определяются из условия равенства площадей круга S3 и квадрата S4:
S3=R2доп – S4 -4X2c - 4Y2c;
(2.42)
Xc
-Yc
= 0,5![]() Rдоп
– 0,89Rдоп.
Rдоп
– 0,89Rдоп.
Замена кругового строба равновеликим квадратным практически не сиазывает влияния на величину вероятности попадания отметки в площадь строба.
При использовании для сопровождения целей одного прямоугольного или квадратного строба его размеры Xc, Yc задаются заранее. Поэтому операции формирования строба и собственно стробирование производятся по более простым предписаниям, нежели в метод дах минимальных эллиптических или круговьк отклонений (рис. 2.26). Стробирование отметок (блоки 1, 2, 3) выполняется по следуютщим правилам:
![]()
![]()
(2.43)
![]()
![]()
Если в площади строба оказывается не более одной отметку (N1), селекция задается по правилам, принятым в методе минимальЧ кых эллиптических отклонений (блоки 4,5,6). При попадании в строй двух и более отметок (N>1) возникает неопределенная ситуация, непосредственно неразрешимая методом одного строба. В подобных случаях для разрешения неопределенности возможно применение приближенных правил отбора.
Так, за продолжение
траектории может быть принята каждая
из находящихся в стробе отметок. Но
это приводит к появлению ложных трасс
(рис.2.20). Селекция отметок может
производиться по
правилу случайного выбора; когда за
вершину траектории принимается любая
из попавших в площадь строба отметок,
например, появившаяся в нем, первой по
времени. При полуавтоматическом
сопровождении применимы и другие, чисто
эвристические правила выбора п
Рис.
2.26.Алгоритм стробирования отметок
целей методом одного строба.
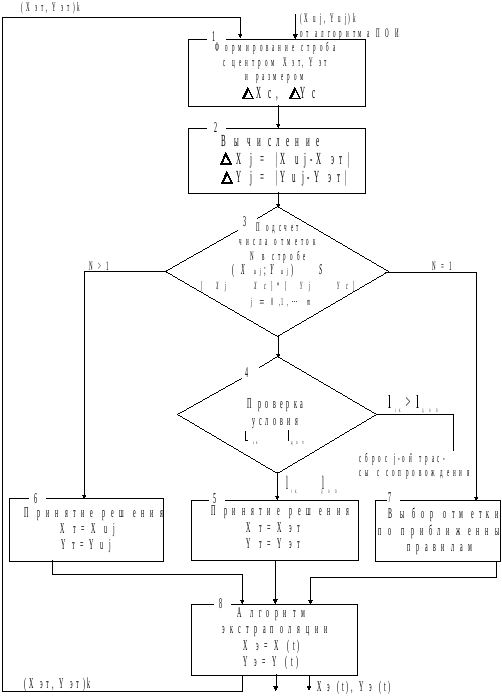
 Рис.
2.27. Селекция отметок методом двух
стробов.
Рис.
2.27. Селекция отметок методом двух
стробов.
Применение в алгоритмах селекции нескольких стробов, с одной стороны, снижает вероятность неправильного сброса трасс с сопровождены при маневрах целей, и с другом - позволяет ограничить количество селектируемых в каждом обзоре отметок за счет выделения для анализа сравнительно небольшой зоны воздушного пространства.
Процесс селекции и стробировааня в случае применения нескольких стробов по многоступенчатой схеме. Седекция отметок на каждой ступени отбора ведется по методу одного строба, так, при использовании двух стробов на первом этапе производится грубый отбор отметок по большому стробу S (рис. 2.27), размеры которого выбраны из условия обеспечения в очередном k-м обзоре максимальной вероятности попадания отметки Ад в площадь строба. Затем из числа попавших в большой строб отметок с помощью малого строба Sm выбирается та, которая с большей вероятностью принадлежит сопровождаемой траектории. Процедура селекции отметок в малом стробе выполняется в соответствии с рассмотренными выше правилами отбора (блоки 4, 5, 6, 7 на рис. 2.26).
