Иванченко

Міністерство освіти і науки України

Департамент науки і освіти Харківської області державної адміністрації

Харківське територіальне відділення МАН України

Відділення: математика

Секція: математика

Геометрія шахової дошки. Шахові фігури.

Роботу виконала:

Іванченко Станіслава Сергіївна,

Учениця 9-А класу

Люботинської гімназії №1

Харківської області

Науковий керівник:

Касьяненко Лілія Григорівна

Учитель математики

Люботинської гімназії №1

Харківської області,

Спеціаліст вищої категорії

Люботин – 2014

ТЕЗИ

Назва роботи: Геометрія шахової дошки. Шахові фігури.

Автор роботи: Іванченко Станіслава Сергіївна

Назва територіального відділення МАН:

Харківське територіальне відділення МАН України

Навальний заклад: Люботинська гімназія №1 Харківської оласті

Населений пункт: м . Люботин Харківської області

Науковий керівник Касьяненко Лілія Григорівна, вчитель математики Люботинської гімназії №1, спеціаліст вищої категорії.

Мета: розповідь про геометрію шахової дошки, введенню швидкостей фігур, а також вивчення їх властивостей.»

Серед скарбниць гробниці Тутанхамона (єгипетського фараона початку XIV ст. до н.е.), можна знайти гральну дошку, яка розділена на 30 квадратів, та фігурки конічної та котушкоподібної форми, що на ній стоять. Гральні дошки знаходили і в більш древніх похованнях Месопотамії. У колекції Британського музею зберігається так званий Папірус Рінда, який був виготовлений єгипетським писарем Ахмесом близько 1550 р. до н.е. (за іншими джерелами - близько 1700 р. до н.е.) і переписаний з більш раннього папірусу. У ньому міститься декілька десятків конкретних математичних задач з їхніми рішеннями (дії з дробами, обчислення довжин та площі). Отже, як ми бачимо, і шахи, і математика сягають своїми коренями в глибоку давнину. Це, звісно ж, лише посереднє, але все ж таки підтвердження спорідненості між ними, яка складається з абстрактного та аксіоматичного характеру математики та шахів.

ЗМІСТ

Вступ………………………………………………..стр. 4

1.Король…………………………………………….стр.5

2. Пішак……………………………………………..стр.7

Висновок……………………………………………стр.8

Список використаних джерел……………………стр.9

ВСТУП

У звичайному житті ми весь час зіштовхуємося з так званою евклідовою геометрією. Однак для шахівниці вона, чесно кажучи, не дуже зручна. Розглянемо найпростіший приклад.

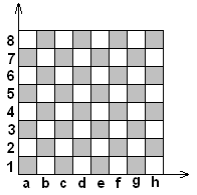(Мал. 1)

Король з поля h1 може дійти до полів g2, h2 и g1 за один хід – див. мал. 2.1.1. Тобто з точки зору ходів короля, відстані між цими клітинами та клітиною h1 рівні. У той час, як в звичайній евклідовій геометрії виконується рівність: h1, g2  √2,h1,h2  h1, g1 1, для ферзя h1, g1  h1,a8 1 , так як і до поля а8, і до поля g1 з поля h1 ферзь може дістатися за один хід. Як бачимо, звичайна геометрія в даному випадку дуже незручна. Існує два способи обійти дану проблему: 1) ввести «швидкість» фігури, як відношення відстані між клітинами та кількості ходів, за яку вона може її подолати, залишивши при цьому правила підрахунку відстаней. При цьому, звичайно ж, у деяких фігур швидкість буде залежати від напрямку руху.

2) відстань між полями шахівниці вимірювати як мінімальну кількість ходів, за яку дана фігура попаде з одного з цих полів на інше. Зрозуміло, що відстань, введена таким чином, залежить від конкретної фігури. Ми зупинимося детальніше на першому способі, оскільки при його вивченні ми все одно будемо вимушені знаходити мінімальну кількість ходів для фігур. Тобто, розглядаючи перший варіант, ми розглянемо і другий. Зауваження: ми будемо описувати результати для «дискретного» випадку, тобто для руху фігур на шахівниці, а потім намагатися природним шляхом узагальнювати їх для неперервного випадку (тобто, якщо фігура рухалась не тільки з клітини в клітину, а в будь-якому напрямку на будь-яку «доступну» їй відстань). При цьому відстані між центрами сусідніх за стороною клітин вважаються рівними 1 ум. од. Крім того, введемо «дискретні» координати: центр поля а1 має координати (0,0), поля а2 - (1,0) і т.д. – м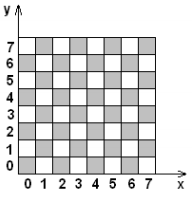ал. 2

(Мал. 2)

Король

Розрахуємо спочатку швидкість короля V_кр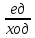 залежно від його напрямку руху. Якщо король рухається з поля (0,0) на поле (x,y), то:   2 2 V_карmax (x, y)=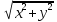, бо дійти до поля (x,y) він може за мінімальну кількість ходів – max(x,y), а відстань між центрами полів (0,0) та (x,y) у звичайній евклідовій геометрії дорівнює:.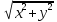

Нехай тепер φ – кут між вектором із координатами (х,у) та віссю Ох, при чому відлік відбувається проти годинникової стрілки.

Тоді: .

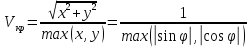З отриманої формули видно, що швидкість короля не залежить від початкової та кінцевої точок його шляху, а залежить лише від кута між прямою, що містить ці точки, та віссю Ох, тобто від напрямку руху. Примітка: Якщо продовжити міркування в цьому напрямку та ввести метрику, яка відповідає отриманій формулі для швидкості короля, можна отримати геометрію Банаха-Мінковського, у якій відстань вимірюється по- різному в різних напрямках.

Це пов’язано з тим, що скориставшись формулами зведення для тригонометричних функцій, у кожному з цих випадків отримаємо в знаменнику виразу для швидкості максимум від синусу та косинусу кута  .

4. При такому введенні V_кр король проходить відстань між полями а і b за таку ж саму кількість ходів, що й відстань між полями b і а.

Такий спосіб задавання V_кр дає можливість легко узагальнити його для неперервного випадку руху короля

.

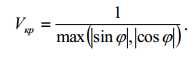Пішак

Обчислимо тепер швидкість руху для пішака.

Зауваження: будемо вважати, що пішак не перетворюється у ферзя (або будь-яку іншу фігуру), коли досягає останньої горизонталі. Якщо пішак рухається з поля із координатами (x,1) (білий пішак) до поля із координатами (x,y), у ≥ 3, то її швидкість:

Бо перший хід пішак робить на 2 клітини вперед (при у ≥ 3) через те, що ми розглядаємо мінімальну кількість ходів.

При у=2: V_п 1. Якщо ж пішак рухається з поля (х, у₀)до поля х, у₁), у₀ ≥ 2, то її швидкість задовольняє наступній умові: V_п y₁  y₀   y₁  y₀ V_п 1 .

Властивості V_п :

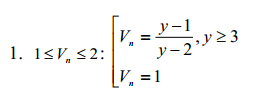
2. V_п залежить від відстані, яку необхідно подолати пішаку тільки якщо вона рухається з другої горизонталі.

3. V_п змінюється в тому випадку, коли пішаку доводиться бити іншу фігуру. У цьому випадку: V_п  2 . Зауважимо, що у короля цього не відбувається. Особливість пішака в тому, що з другої горизонталі він може зробити хід одразу на дві клітини. Це заважає узагальнити закон його руху для неперервного випадку. Однак у більшості випадків можна вважати швидкість пішака V_п  1, особливо при русі на великі відстані.

Висновок: У даній роботі були представлені досліди деяких особливостей геометрії шахової дошки, розглянуті способи застосування отриманих результатів та намічені шляхи подальшого розвитку даної теми. Введення швидкостей шахових фігур дозволило використовувати при обчисленнях звичайну евклідову геометрію, що значно полегшило самі обчислення.

Список літератури

[1] Е.Я. Гик. Математика на шахматной доске.

http://www.wysotsky.com/0009/536.htm

[2] І. М. Мітельман. Розфарбуємо клітчасту дошку.

http://matematuka.inf.ua/konkurs/mitelman/mitelman_rozf.html

9