1. Основные матричные операции

Основными матричными операциями являются умножение матрицы на число, сложение и перемножение двух матриц.

По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.

Суммой двух матрицодинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Операция умножения матрицы на матрицу определяется более сложным образом. Пусть заданы две матрицы А и В, причём число столбцов первой из них равно числу строк второй. Если

, ,

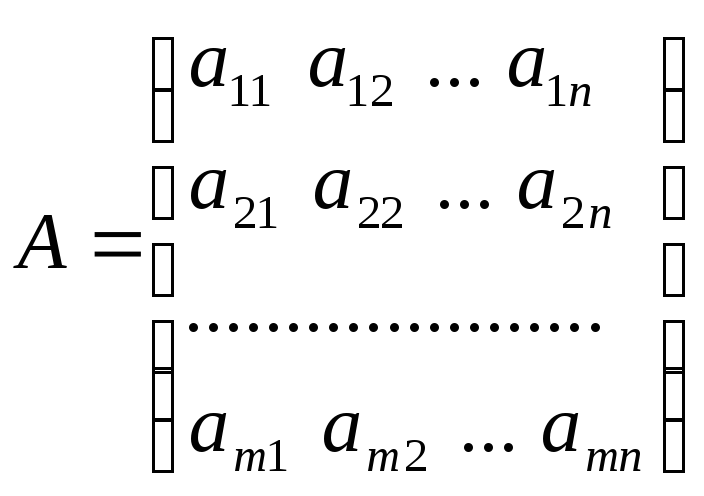то произведением матриц А и В называется матрица

,

элементы которой вычисляются по формуле

c_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj , где i = 1,…,m, j = 1,…,k.

Единичная матрица– это квадратная матрица, все диагональные элементы которой – единицы, а остальные – нули:

Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица – частный случай скалярной матрицы.

Для прямоугольных матриц определена операция транспонирования. Рассмотрим прямоугольную матрицу А. Матрица, получающаяся из матрицы А заменой строк столбцами, называется транспонированной по отношению к матрице А и обозначается А^Т:

, .

Квадратная матрица А называется обратимой, если существует квадратная матрица Х, удовлетворяющая соотношениям АХ = ХА = Е, где Е – единичная матрица. Матрица Х называется обратной к матрице А и обозначается А^-1, т.е. АА^-1 = А^-1А = Е.

Квадратная матрица А, для которой А^-1 = А, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.

Квадратная матрица М, для которой М^-1 = М^Т, называется ортогональной матрицей. Модуль определителя ортогональной матрицы равен единице; сумма квадратов элементов любого столбца ортогональной матрицы равна единице; сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна нулю. Такими же свойствами обладают строки ортогональной матрицы.

2. Определители и их свойства

Пусть А – квадратная матрица порядка n, n > 1:

.

Определителем квадратной матрицы А порядка n, n > 1, называется число

=,

где - определитель квадратной матрицы порядкаn - 1, полученной из матрицы А вычёркиванием первой строки и j-го столбца.

Из приведённого определителя легко получить простое выражение определителя квадратной матрицы второго порядка через элементы матрицы:

,

поскольку ,.

Например:

Формулу detA= называют формулой вычисления определителя разложением по первой строке. Число называется алгебраическим дополнением элемента.

Пусть - определитель квадратной матрицы порядка n - 1, полученной из матрицы А вычёркиванием i-ой строки и j-го столбца; число называется алгебраическим дополнением элементаматрицыА. Справедливо следующее утверждение.

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения, т.е. для произвольной квадратной матрицы порядка n для всех i, 1 ≤ I ≤ n, и для всех j, 1 ≤ j ≤ n, справедливы формулы:

=.

Приведённые формулы называют формулами вычисления определителя разложением по i-ой строке и разложением по j-му столбцу соответственно.

Приложение В

Решение системы линейных алгебраических уравнений по формулам Крамера.

При решении задач линейной алгебры часто возникает необходимость вычислять определитель. Рассмотрим решение линейных систем по формулам Крамера. Пусть

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n = b₁,

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n = b₂,

……………………………..

a_n1x₁ + a_n2x₂ + … + a_nnx_n = b_n

система n линейных алгебраических уравнений относительно n неизвестных x₁, x₂, …, x_n.

Матрица

Называется матрицей системы, а вектор-столбец =(b₁ b₂ … b_n)^Т – столбцом правых частей системы. Рассмотренная система линейных алгебраических уравнений может быть записана в матричной форме в виде , где – вектор-столбец неизвестных,= (х₁ х₂ … х_n)^Т.

Справедливо следующее утверждение. Если определитель ∆=detА матрицы системы отличен от нуля, то система имеет единственное решение х₁ х₂ … х_n, определяемое формулами Крамера , где∆_I – определитель матрицы n-го порядка, полученной из матрицы системы заменой i-го столбца столбцом правых частей.

Приложение С