
- •Вопросы к госэкзамену
- •1. Конечные цифровые автоматы (ца). Абстрактный автомат как математическая модель конечного ца. Автоматы Мили и Мура, с-автомат, законы функционирования, основные отличия. Варианты ца.
- •2. Способы задания ца. Задание цифровых автоматов на начальных языках: язык граф схем алгоритмов (гса) и язык логических схем алгоритмов (лса).
- •Табличный способ задания.
- •4. Автомат без памяти (комбинационная схема). Закон функционирования, этапы проектирования. Основные критерии качества технической реализации.
- •5.Канонический метод синтеза комбинационных схем (кс). Синтез кс в булевом базисе, базисах и-не, или-не, и-или-не. Правила преобразования для рациональной реализации.
- •Можно привести схемы.
- •6. Абстрактный синтез ца. Представление автоматов на стандартном языке на основе задания его на начальном языке. Построение таблиц переходов по гса.
- •7. Абстрактный синтез ца. Представление автоматов на стандартном языке на основе задания его на начальном языке. Построение таблиц переходов по лса.
- •8. Операционное устройство как модель дискретного преобразователя в.М. Глушкова. Операционные и управляющие автоматы. Микропрограммные автоматы. Принцип микропрограммного управления.
- •9. Управляющие автоматы (уа) с жесткой логикой. Взаимодействие автомата с внешней средой. Синхронизация автоматов. Гонки или состязания в автоматах. Методы устранения гонок.
- •10. Управляющие автоматы (уа) с программируемой логикой. Структурная организация. Способы адресации микрокоманд.
7. Абстрактный синтез ца. Представление автоматов на стандартном языке на основе задания его на начальном языке. Построение таблиц переходов по лса.
На этапе абстрактного синтеза по алгоритму, заданному на начальном языке, строится таблица переходов, записываются система канонических уравнений (СКУ) и система выходных функций (СВФ) и проводится их минимизация. Для интерпретации микропрограммы можно использовать автомат Мили или автомат Мура.
Методика построения таблицы переходов по ЛСА:
1) Пронумеровать
все операторные вершины ЛСА. Если в ЛСА
имеются циклы из из логический условий
, то вводится пустой оператор Ae (ye),
отмеченный пустым выходным сигналом.
Этот оператор помещают в ЛСА путём
замены стрелки
![]() ,
стоящей в начале петли из логический
условий на следующую группу символов
ЛСА:
,
стоящей в начале петли из логический
условий на следующую группу символов
ЛСА:
Например,
скорректируем ЛСА
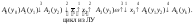
получим:

2) Каждому оператору ЛСА поставить в соответствие вполне определенное состояние автомата. Причем одинаковым операторам, стоящим в разных местах ЛСА, должны соответствовать разные состояния. Это обеспечивается сквозной нумерацией операторов ЛСА. Начальному оператору будет соответствовать исходное состояние автомата.
3) Осуществляется просмотр всех путей перехода, ведущих от одного оператора к другому. Причем, каждый такой путь должен соответствовать шагу алгоритма и состоять только из логических условий.
Каждому пути из логических условий от одного оператора к другому сопоставить конъюнкцию входных сигналов. Причем в конъюнкцию логических переменных xi войдет с отрицанием или без:
а) без отрицания, если xi = 1 (логическое условие истинно), тогда проверяется следующая по порядку записи логическая переменная (логическое условие), если она находится в строке;
б) с отрицанием,
если xi
= 0
(логическое условие ложно), тогда
проверяется по стрелке, стоящей справа
от
![]() ,
следующая логическая переменная
(логическое условие), стоящая справа от
конца стрелки
,
следующая логическая переменная
(логическое условие), стоящая справа от
конца стрелки![]() .
.
Если в ЛСА имеется
безусловный переход, например, для
фрагмента ЛСА
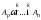 ,
то путь от исходного оператораAp
до конечного в конце пути An
определится концом стрелки безусловного
перехода.
,
то путь от исходного оператораAp
до конечного в конце пути An
определится концом стрелки безусловного
перехода.
4. Построить таблицу переходов автомата Мура. Для этого необходимо анализировать все полученные пути между операторами, учитывая, что каждый оператор отмечен совокупностью выходных сигналов.
Пример.
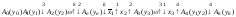
|
Таблица переходов автомата Мура |
|
СКУ: a1(t+1) = a0; a2(t+1)
= a1 a3(t+1)
= a2
a4(t+1)
= a2
a5(t+1)
= a2
x1x3 a6(t+1)
= a2
x1
СВФ: y0= a0; y1
= a1 y2
=
a2 y3 = a4; ye = a3; yk = a6. | |||||
|
ai(t) |
yi(t) |
xij(t) |
aj(t+1) |
|
| ||
|
a0 |
y0 |
1 |
a1 |
|
| ||
|
a1 |
y1 |
1 |
a2 |
|
| ||
|
a2 |
y2 |
x1 x3 x1
|
a5 a6 a4 a3 |
|
| ||
|
a3 |
ye |
x1 x3 x1
|
a5 a6 a4 a3 |
|
| ||
|
a4 |
y3 |
1 |
a2 |
|
| ||
|
a5 |
y1, y2 |
1 |
a6 |
|
| ||
8. Операционное устройство как модель дискретного преобразователя в.М. Глушкова. Операционные и управляющие автоматы. Микропрограммные автоматы. Принцип микропрограммного управления.
При описании функционирования операционного устройства (ОУ) часто используется его представление моделью Глушкова В.М., состоящей из двух тесно взаимодействующих блоков в соответствии рис. 1.1. Один из них выполняет функции операционного автомата (ОА), а другой управляющего автомата (УА). Такой подход упрощает проектирование, а также облегчает понимание процесса функционирования операционного устройства.
УА и ОА вместе образуют цифровой процессор. Если цифровой процессор универсальный и предназначен для выполнения арифметических операций, то код операции (КОП) определяет, какую именно операцию будет выполнять процессор при подаче сигнала "Пуск".

Операционный автомат (ОА) является исполнительной частью устройства, т. е. реализует действия над исходной информацией, получаемой, с целью получения результатов.
ОА состоит из регистров, сумматоров и других узлов, которые производят прием из оперативной памяти через шину данных (ШД) и хранение кодов исходных операндов их преобразование согласно реализуемому алгоритму и выдачу в оперативную память результата преобразования. ОА вычисляет и выдает в УА осведомительные сигналы X={x1,x2, … ,xL}, которые характеризуют состояния узлов ОА после выполнения очередного шага алгоритма (например, равенство нулю результата операции, переполнение сумматора и др.).
Управляющий автомат (УА) генерирует распределенную во времени последовательность управляющих сигналов Y={y1,y2, …, yM}, которые порождают в ОА выполнение соответствующей алгоритму последовательности микроопераций. То есть УА задает порядок выполнения действий в ОА.
Последовательность управляющих сигналов определяется функциями перехода УА, которые зависят от сигналов кода операции q, поступающих в УА извне, и значений осведомительных сигналов X={xi}, характеризующих состояния узлов ОА.
Функциональная и структурная организация операционных устройств базируется на принципе микропрограммного управления, который состоит в следующем.
1. Любая операция, реализуемая ОУ, рассматривается в виде последовательности элементарных неделимых актов обработки информации, выполняемых в течение одного такта автоматного времени (одного шага алгоритма) и называемых микрооперациями. Примеры микроопераций: «Сдвиг кода числа», «Инвертирование кода числа» и т.д. Микрооперации, реализуемые в ОА, инициируются множеством управляющих сигналов Y={y1,y2, …, yM}, с каждым из которых отождествляется определенная микрооперация.
Если в ОА одновременно реализуются несколько микроопераций, то это подмножество микроопераций называют микрокомандой. В этом случае в ОА могут поступать несколько управляющих сигналов, вызывая параллельное во времени выполнение нескольких микроопераций. Не исключен случай, когда множество микроопераций, образующих микрокоманду пусто. Реализация такой микрокоманды в ОА равносильна отсутствию выполнения каких-либо микроопераций. В случае синхронных цифровых автоматов пустая микрокоманда интерпретируется как пропуск такта, когда никакие управляющие сигналы в УА не поступают.
2. Для управления порядком следования микрокоманд используются логические условия, которые в зависимости от результатов преобразования информации в ОА могут принимать значения 1 или 0. Множество логических условий обозначают символами X={x1,x2, …, xL} и называют осведомительными сигналами.
3. Алгоритм выполнения операций в устройстве, записанный в терминах микроопераций и логических условий, называется микропрограммой. Микропрограмма определяет порядок проверки логических условий и следования микроопераций и используется как форма представления функции операционного устройства, на основании которой определяется структура и порядок функционирования устройства во времени.
Использование принципа микропрограммного управления, который рассматривает процесс функционирования устройства как процесс реализации микроопераций и проверки логических условий, определяемый микропрограммой, позволяет упорядочить и формализовать проектирование операционных устройств различного назначения.
Конечный автомат, реализующий микропрограмму работы дискретного устройства, принято называть микропрограммным автоматом.

 a4;
a4; 1
1 2
2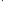 a3
a3 1
1 2;
2; 1x
2
1x
2 a3
a3
 1x2;
1x2; a3
x1x3;
a3
x1x3; 3
3 a3
x1
a3
x1 3
3 a5.
a5.
 a5;
a5; a5;
a5; 3
3 1x2
1x2 1
1 2
2 3
3 1x2
1x2 1
1 2
2