
- •-ХКолебания и волны. Звук. Ультразвук.
- •3. Свободные и вынужденные колебания. Собственная частота колебаний системы. Явление резонанса. Примеры.
- •4. Физические и психофизические характеристики звука: интенсивность, акустическое давление, частота, громкость, высота тона, спектр, тембр. Их взаимное соответствие.
- •5. Особенности восприятия звука. Закон Вебера-Фехнера. Децибельная шкала громкости.
- •Закон Вебера-Фехнера.
- •Децибельная шкала
- •6. Звуковые методы исследования в медицине: перкуссия, аускультация. Фонокардиография.
- •Аускультация
- •Перкуссия
- •Фонокардиография
- •7. Ультразвук. Получение и регистрация ультразвука на основе обратного и прямого пьезоэлектрического эффекта.
- •8. Взаимодействие ультразвука различной частоты и интенсивности с веществом. Применение ультразвука в медицине.
- •Электромагнитные колебания и волны.
- •4.Шкала электромагнитных волн. Классификация частотных интервалов, принятая в медицине
- •5.Биологическое действие электромагнитного излучения на организм. Электротравматизм.
- •6.Диатермия. Увч-терапия. Индуктотермия. Микроволновая терапия.
- •7.Глубина проникновения неионизирующих электромагнитных излучений в биологическую среду. Ее зависимость от частоты. Методы защиты от электромагнитных излучений.
- •Медицинская оптика
- •1. Физическая природа света. Волновые свойства света. Длина световой волны. Физические и психофизические характеристики света.
- •2. Отражение и преломление света. Полное внутреннее отражение. Волоконная оптика, ее применение в медицине.
- •5. Разрешающая способность и предел разрешения микроскопа. Пути повышения разрешающей способности.
- •6. Специальные методы микроскопии. Иммерсионный микроскоп. Микроскоп темного поля. Поляризационный микроскоп.
- •Квантовая физика.
- •2. Линейчатый спектр излучения атомов. Его объяснение в теории н.Бора.
- •3. Волновые свойства частиц. Гипотеза де-Бройля, ее экспериментальное обоснование.
- •4. Электронный микроскоп: принцип действия; разрешающая способность, применение в медицинских исследованиях.
- •5. Квантово-механическое объяснение структуры атомных и молекулярных спектров.
- •6. Люминесценция, ее виды. Фотолюминесценция. Закон Стокса. Хемилюминесценция.
- •7. Применение люминесценции в медико-биологических исследованиях.
- •8. Фотоэлектрический эффект. Уравнение Эйнштейна для внешнего фотоэффекта. Фотодиод. Фотоэлектронный умножитель.
- •9. Свойства лазерного излучения. Их связь с квантовой структурой излучения.
- •10. Когерентное излучение. Принципы получения и восстановления голографических изображений.
- •11. Принцип работы гелий-неонового лазера. Инверсная населенность энергетических уровней. Возникновение и развитие фотонных лавин.
- •12. Применение лазеров в медицине.
- •13. Электронный парамагнитный резонанс. Эпр в медицине.
- •14. Ядерный магнитный резонанс. Использование ямр в медицине.
- •Ионизирующие излучения
- •1. Рентгеновское излучение, его спектр. Тормозное и характеристическое излучение, их природа.
- •3. Применение рентгеновского излучения в диагностике. Рентгеноскопия. Рентгенография. Флюорография. Компьютерная томография.
- •4. Взаимодействие рентгеновского излучения с веществом: фотопоглощение, когерентное рассеяние, комптоновское рассеяние, образование пар. Вероятности этих процессов.
- •5. Радиоактивность. Закон радиоактивного распада. Период полураспада. Единицы активности радиоактивных препаратов.
- •6 Закон ослабления ионизирующих излучений. Коэффициент линейного ослабления. Толщина слоя половинного ослабления. Массовый коэффициент ослабления.
- •8. Получение и применение радиоактивных препаратов для диагностики и лечения.
- •9. Методы регистрации ионизирующего излучений: счетчик Гейгера, сцинтилляционный датчик, ионизационная камера.
- •10. Дозиметрия. Понятие о поглощенной, экспозиционной и эквивалентной дозе и их мощности. Единицы их измерения. Внесистемная единица – рентген.
- •Биомеханика.
- •1. Второй закон Ньютона. Защита организма от избыточных динамических нагрузок и травматизма.
- •2. Виды деформации. Закон Гука. Коэффициент жесткости. Модуль упругости. Свойства костных тканей.
- •3. Мышечные ткани. Строение и функции мышечного волокна. Преобразование энергии при мышечном сокращении. Кпд мышечного сокращения.
- •4. Изотонический режим работы мышц. Статическая работа мышц.
- •5. Общая характеристика системы кровообращения. Скорость движения крови в сосудах. Ударный объем крови. Работа и мощность сердца.
- •6. Уравнение Пуазейля. Понятие о гидравлическом сопротивлении кровеносных сосудов и о способах воздействия на него.
- •7. Законы движения жидкости. Уравнение неразрывности; его связь с особенностями системы капилляров. Уравнение Бернулли; его связь с кровоснабжением мозга и нижних конечностей.
- •8. Ламинарное и турбулентное движение жидкости. Число Рейнольдса. Измерение артериального давления по методу Короткова.
- •9. Уравнение Ньютона. Коэффициент вязкости. Кровь как неньютоновская жидкость. Вязкость крови в норме и при патологиях.
- •Биофизика цитомембран и электрогенеза
- •1. Явление диффузии. Уравнение Фика.
- •2. Строение и модели клеточных мембран
- •3. Физические свойства биологических мембран
- •4. Концентрационный элемент и уравнение Нернста.
- •5. Ионный состав цитоплазмы и межклеточной жидкости. Проницаемость клеточной мембраны для различных ионов. Разность потенциалов на мембране клетки.
- •6. Потенциал покоя клетки. Уравнение Гольдмана-Ходжкина-Катца
- •7. Возбудимость клеток и тканей. Методы возбуждения. Закон «все или ничего».
- •8. Потенциал действия: графический вид и характеристики, механизмы возникновения и развития.
- •9. Потенциал-зависимые ионные каналы: строение, свойства, функционирование
- •10. Механизм и скорость распространения потенциала действия по безмякотному нервному волокну.
- •11. Механизм и скорость распространения потенциала действия по миелинизированному нервному волокну.
- •Биофизика рецепции.
- •1. Классификация рецепторов.
- •2. Строение рецепторов.
- •3. Общие механизмы рецепции. Рецепторные потенциалы.
- •4. Кодирование информации в органах чувств.
- •5. Особенности светового и звукового восприятия. Закон Вебера-Фехнера.
- •6. Основные характеристики слухового анализатора. Механизмы слуховой рецепции.
- •7. Основные характеристики зрительного анализатора. Механизмы зрительной рецепции.
- •Биофизические аспекты экологии.
- •1. Геомагнитное поле. Природа, биотропные характеристики, роль в жизнедеятельности биосистем.
- •2. Физические факторы, имеющие экологическую значимость. Уровни естественного фона.
- •Элементы теории вероятности и математической статистики.
- •Свойства выборочного среднего
2. Физические факторы, имеющие экологическую значимость. Уровни естественного фона.
Экология – это условия окружающей среды, в которых находится биосистема.
Физические экологические факторы (по происхождению):
-геофизические →метеорологические→Земные
-космические: солнечные, космические
-антропогенные
Физические экологические факторы (по физ.сущности):
1. поля:
магнитные поля (силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения.)
гравитационные поля (физическое поле, через которое осуществляется гравитационное взаимодействие (Гравитация —универсальноефундаментальное взаимодействиемежду всеми материальными телами)
электрические поля →ЭМ: радиоизлучение, телевизионный диапазон, локаторы, УФ облучение (на ДНК кожное облучение)
2. вибрация (механическиеколебания.)
3. радиация
инфразвук (упругие волны, аналогичные звуковым, но с частотами ниже области слышимых человеком частот. Обычно за верхнюю границу инфразвуковой области принимают частоты 16—25 Гц)
ультразвук (упругие звуковыеколебания высокойчастоты)
4. звуковые факторы
5. шумовые факторы
Элементы теории вероятности и математической статистики.
Случайные события. Относительная частота наступления события. Закон больших чисел.
Случайное событие – это событие А, которое при выполнении определённого условия Sможет произойти, а может и не произойти, например, выпадение определённой стороны монеты при её подбрасывании, выпадение определённого числа на игральном кубике.
Вероятность Р(А) в теории вероятности выступает как числовая характеристика степени возможности появления какого-либо определённого случайного события А при многократном повторении испытаний. Когда случайное событие А происходит mраз в серииnнезависимых испытаний, относительной частотой события в данной серии испытаний или просто частотой события А называют отношение:
P*(A)=m/n
 Закон
больших чисел: если число испытанийn∞, то относительная частота стремится
к пределу, который называется вероятностью
наступления А в определённых условиях.
Закон
больших чисел: если число испытанийn∞, то относительная частота стремится
к пределу, который называется вероятностью
наступления А в определённых условиях.
limὐ(A)n→∞ = lim nA/n n→∞ = P(A)
Несовместимые события. Примеры. Теорема сложения вероятностей.
Несовместимыми называются события, которые вместе не наступают. Например, одновременное выпадение на одном игральном кубике и 1 и 2, или при подбрасывании монеты одновременное выпадение и орла и решки, или одновременное нахождение одного человека в Петербурге и в Москве.
Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей.
Для двух несовместных событий
Р(А или В) = Р(А) +Р(В)
Доказательство:
Пусть n– общее число испытаний,m1– число случаев, благоприятствующих событию А,m2– число случаев, благоприятствующих событию В. Число случаев, благоприятствующих наступлению либо события А, либо события В, равноm1 +m2. Тогда
Р(А или В) = (m1+m2)/n=m1/n+m2/n.
Отсюда, учитывая, что P(A)=m/n, имеем:
Р(А или В) =Р(А) +Р(В)
Независимые события. Примеры. Теорема умножения вероятностей.
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если значение одной из них не влияет на вероятность значений другой.
Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом:
 :
монеты 1 и 2 упали одной и той же стороной;
:
монеты 1 и 2 упали одной и той же стороной; :
монеты 2 и 3 упали одной и той же стороной;
:
монеты 2 и 3 упали одной и той же стороной;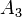 :
монеты 1 и 3 упали одной и той же стороной;
:
монеты 1 и 3 упали одной и той же стороной;
Легко
проверить, что любые два события из
этого набора независимы. Все же три в
совокупности зависимы, ибо зная, например,
что события ![]() произошли,
мы знаем точно, что
произошли,
мы знаем точно, что ![]() также
произошло.
также
произошло.
Теорема умножения вероятностей : вероятность совместного поведения независимых событий равна произведению их вероятностей .для 2 событий P(A и B)= Р(А)* Р(В)
Непрерывная случайная величина. Плотность вероятности. Условие нормировки.
Непрерывная случайная величина принимает любые значения внутри некоторого интервала : tтела ,масса зерен в колосьях пшеницы ,координата места попадания пули в цель(принимаем пулю за материальную точку )
Пло́тность
вероя́тности —
один из способов задания вероятностной
меры на евклидовом
пространстве ![]() .
В случае, когда вероятностная мера
является распределением
случайной величины,
говорят о плотности случайной
величины.
.
В случае, когда вероятностная мера
является распределением
случайной величины,
говорят о плотности случайной
величины.
Выборка. Генеральная совокупность. Требования к выборкам.
Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.
Характеристики выборки:
Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.
Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.
Генеральная совокупность, генеральная выборка (от лат. generis — общий, родовой)(в англ. терминологии — population) — совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.
Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность - это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, женщины 10-89 лет, использующие крем для рук определённых марок не реже раза в неделю, и имеющие доход не ниже $150 на одного члена семьи.
Требования, предъявляемые к выборке.
К генеральной совокупности обычно применимо требование правильного определения ее КОНТУРА. Это означает, что исследователь обязан ответить на два вопроса: охватывает ли он в своих предположениях все возможные элементы генеральной совокупности, и нет ли элементов избыточных, лишних.
Понятие средневыборочного значения и математического ожидания случайной величины.
Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.
Пусть ![]() — выборка из распределения
вероятности, определённая на
некотором вероятностном
пространстве
— выборка из распределения
вероятности, определённая на
некотором вероятностном
пространстве ![]() .
Тогда её выборочным средним
называется случайная
величина
.
Тогда её выборочным средним
называется случайная
величина
![]() .
.
