Свойства выборочного среднего

Пусть  — выборочная функция распределения данной выборки. Тогда для любого фиксированного функция является (неслучайной) функцией дискретного распределения. Тогда математическое ожидание этого распределения равно .

Выборочное среднее — несмещённая оценка теоретического среднего:

.

Выборочное среднее — сильно состоятельная оценка теоретического среднего:

почти наверное при .

Выборочное среднее — асимптотически нормальная оценка. Пусть дисперсия случайных величин конечна и ненулевая, то есть . Тогда

по распределению при ,

где  — нормальное распределение со средним и дисперсией .

Выборочное среднее из нормальной выборки — эффективная оценка её среднего.

7. Характеристики разброса в выборках: размах, дисперсия, среднеквадратичное отклонение.

1)Размах- разность между последним и первым членом выборки:

∆X=X_m-X₁

2) Выборочная дисперсия- среднее арифметическое квадратов отклонения вариант от их среднего значения:

_{k _}

D_в=1/n∑ (x_i–x_в)²

_i=1

3)Среднеквадратичное откланение- квадратный корень из выборочной дисперсии:

σ= корень из D

8. Понятие о нормальном распределении случайной величины.

Нормальное распределение, также называемое гауссовым распределением, гауссианой или распределениемГаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия

9. Гистограмма. Свойства гистограмм.

Гистограмма- столбчатая диаграмма- один из видов графического изображения статистического распределения случайных величин. Изображает зависимость частоты попадания элементов выборки от соответствующего интервала группировки. Гистограмма представляет собой совокупность смежных прямоугольников с основаниями одинаковой протяженности. Основание прямоугольника соответствует некоторому дивпозону значений случайной величины.

Свойства:

1. Показывает в каких диапазонах значений случайная величина наблюдается чаще, а в каких- реже.

2. Показывает в каких диапазонах значений случайная величина будет наблюдаться чаще, а в каких реже. В этом прогностическая ценность гистограмм.

10. Понятие доверительного интервала. Уровень значимости. доверительная вероятность.

надёжностью, в котором с определенной вероятностью p находится средняя. Иначе говоря, р определяет вер. , с которой осуществляются неравенства:

_ _ _

X_в -ԑ< x_г< x_в+ԑ

Уровень Значимости выражает непопадания генеральной средней в доверительный интервал.

β = 1-р

Доверительная вероятность а выражается числом от 0 до 1 ( реже в процентах от 0 до 100) и показывает вероятность того, что действительное значение исследуемой переменной будет лежать в принятом ( указанном) диапазоне.

11. Однородные и неоднородные выборки. Проверка однородности.

Выборка называется однородной, если все её прецеденты одинаково распределёны, то есть выбраны из одного и того же распределения .

Неоднородность означает, что выборки принадлежат различным законам распределения, которые различаются или только параметрами при одном и том же виде, или видом и параметрами распределения.

Проверка однородности.

Вычисляют средние арифметические в каждой выборке

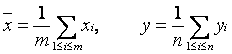
затем выборочные дисперсии

,

и статистику Стьюдента t, на основе которой принимают решение,

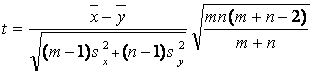
По заданному уровню значимости a и числу степеней свободы (m+n - 2) из таблиц распределения Стьюдента находят критическое значение tкр. Если |t|>tкр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t|<tкр, то принимают. (При односторонних альтернативных гипотезах вместо условия |t|>tкр проверяют, что t>tкр; эту постановку рассматривать не будем, так как в ней нет принципиальных отличий от обсуждаемой здесь.)

12. Виды связи между двумя переменными: корреляционная, функциональная. Примеры.

- функциональная-если данному значению одной велечины соответствует вполне определенное значение другой

Например: площадь круга зависит от радиуса, ускорение тела-от силы и массы

- корреляционная-статистическая взаимосвязь двух или нескольких случайных величин

Например:между возрастом и ростом детей выражается в том, что каждому значению возраста соответствует определенное распределение роста. При этом с увеличением возраста возрастает и среднее значение роста.

13. Понятие о коэффициенте коррелиции. Его свойства.

Наличие связей между X и Y, характер этой связи и ее теснота оценивается коэффициентом корреляции.

Свойства:

1. если связ между X и Y отсутствует, то r=0

2. -1_<r­_<+1; 0_<|r|_<1

3. для возрастающих Y (x) r>0

4. для убывающих Y (x) r<0

5. Предельно тесная связь Xи Y функциональная; при этом r=1 или r=-1

6. коэффициент корреляции описывается линейную связь, но не более сложную

7. Если корреляционная связь Y (x) установлена, она может быть описана уравнением регрессии вида

y=ax+b

14. Понятие о линейной регрессии. Уравнение линейной регрессии и его график.

Линейная регрессия — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.

Формула: y=ax+b

График: