
- •1. Общие понятия и основные положения
- •1.Основные гипотезы в сопротивлении материалов.
- •2.Внешние силы и их классификация.
- •3.Основные объекты, изучаемые в сопромате.
- •4.Понятие о расчетной схеме.
- •5.Внутренние силы. Метод мысленных сечений. Напряжение полное, нормальное и касательное. Размерность напряжения.
- •6.Деформации и перемещения. Деформации линейные и угловые.
- •7.Принцип независимости действия сил.
- •2. Растяжение и сжатие прямого бруса
- •2. Осевой, полярный и центробежный моменты инерции. Моменты инерции для квадрата, прямоугольника, треугольника и круга.
- •3) Определение моментов инерции относительно параллельных и повёрнутых координатных осей.
- •Напряжения по наклонным площадкам
- •2. Внутренние силы в поперечных сечениях бруса при изгибе: изгибающие моменты и поперечные силы. Чистый изгиб и поперечный изгиб. Дифференциальные зависимости при изгибе.
- •3. Построение эпюр внутренних усилий для балок, брусьев ломанного и криволинейного очертания.
- •4. Правила контроля правильности построения эпюр внутренних усилий при изгибе.
- •5. Нормальные напряжения при чистом изгибе. Основные гипотезы. Формула нормальных напряжений. Эпюра распределения нормальных напряжений по высоте поперечного сечения.
- •6. Касательные напряжения при изгибе (формула Журавского). Эпюра распределения касательных напряжений по высоте поперечного сечения.
- •7. Анализ напряжённого состояния при изгибе. Главные напряжения при изгибе. Траектория главных напряжений.
- •8. Расчет на прочность при изгибе. Подбор сечения. Рациональное сечение балок.
- •9. Определение перемещений при изгибе, универсальные уравнения углов поворота сечения и прогибов.
- •6. Сдвиг
- •1. Напряжения и деформации при сдвиге. Закон Гука при сдвиге, модуль сдвига.
- •2. Зависимость между относительным сдвигом и относительными линейными деформациями. Зависимость между g, e, µ для изотропного тела
- •3) Расчёт на прочность заклёпочных и сварных соединений.
- •7. Кручение
- •1.Внешние силы, вызывающие кручение прямого бруса. Эпюры крутящих моментов.
- •2. Кручение прямого бруса круглого поперечного сечения. Основные гипотезы. Определение касательных напряжений. Эпюры распределения касательных напряжений.
- •Основные гипотезы:
- •Эпюры распределения касательных напряжений
- •Ip - полярный момент инерции
- •3.Определение угла закручивания при кручении. Жесткость при кручении. Главные напряжения и главные площадки. Закон Гука при кручении.
- •4. Особенности разрушения пластичных и хрупких материалов при растяжении и кручении.
- •5. Статически неопределимые задачи при кручении.
- •6. Расчеты на прочность и жесткость при кручении.
- •8. Сложное сопротивление
- •1. Расчет на прочность при косом изгибе
- •1) Сравнить любое напряженное состояние с простым растяжением или сжатием;
- •2) Установить причины разрушения материала элементов конструкций в реальных условиях.
- •2. Классические критерии прочности и пластичности
- •Критерий наибольших нормальных напряжений (1-ая теория прочности).
- •2. Действительный вид зависимости критического напряжения от гибкости.
- •3. Практический метод расчета на устойчивость.
- •По этой формуле можно решать два типа задач:
- •10. Действие динамических нагрузок
- •1) Учет сил инерции при поступательном, равноускоренном и равномерном движении по окружности. Принцип Даламбера
- •2) Ударные действия нагрузок.
- •3) Расчеты на прочность, при напряжениях, переменных во времени.
6.Деформации и перемещения. Деформации линейные и угловые.
Деформация - изменение формы и размеров тела, возникающие при приложении к рассматриваемому телу внешних сил.
Деформации разделяются на упругие и остаточные. Упругими деформациями называются такие изменения формы и размеров тела, которые исчезают после удаления вызвавших их сил, и тело полностью возвращается в первоначальную форму. Те деформации, которые остаются в теле после удаления внешних сил, называются остаточными.
Перемещение - изменение положения точки тела в пространстве вследствие изменения его формы и размеров под действием нагрузки.
Линейная деформация - характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.
Угловая деформация - характеризует изменение формы тела и чаще всего называется углом сдвига.
Угол сдвига — это изменение первоначально прямого угла. γ = α + β .
Полная деформация — это сумма линейной и угловой деформации.
7.Принцип независимости действия сил.
Для рассчитываемых реальных объектов (линейно деформируемых систем) справедливо утверждение, которое называется принципом независимости действия сил(принципом суперпозиции или наложения). Этот принцип применяется тогда, когда упругие деформации конструкции достаточно малы и они не вызывают изменения в расположении нагрузок, считается справедливым закон Гука. В этом случае результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности.
2. Растяжение и сжатие прямого бруса
1. Принцип Сен-Венана, гипотеза Бернулли
Принцип Сен-Венана – напряжение в местах достаточно удалённых от мест приложения нагрузки распределяется равномерно.
Гипотеза Бернулли – поперечные сечения, плоские до деформации, остаются плоскими и после деформации (гипотеза Плоских сечений).
2. Определение внутренних усилий. Эпюры продольных сил.
Внутреннее усилие численно равно алгебраической сумме всех сил, расположенных по одну сторону от рассматриваемого сечения (метод сечений).По двум точкам строим эпюру N.
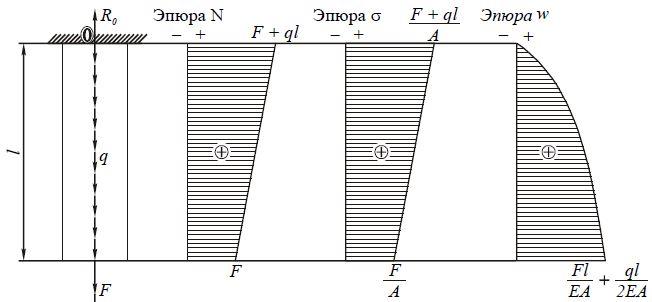
3. Определение напряжений, эпюра напряжений.
Напряжения численно равны усилию на участке, деленному на площадь этого участка
![]()
4. Напряжения в наклонных сечениях к оси бруса.
![]() ;
;
![]() ;
;
5. Закон Гука при растяжении сжатии. Модуль упругости Е и коэффициент Пуассона μ. Жёсткость при растяжении и сжатии.
Закон Гука – абсолютное удлинение (укорочение) стержня прямо пропорционально действующей силе, длине стержня и обратно пропорционально произведению ЕА, называемому ЖЁСТКОСТЬЮ стержня при растяжении и сжатии.
![]() ;
;
![]() ;
;![]() ;
;
E-модуль Юнга – коэффициент пропорциональности.
Коэффициент Пуассона – Отношение относительной поперечной деформации к относительной продольной деформации взятое по абсолютной величине. μ=|εпоп/εпрод|
6. Перемещение поперечных сечений бруса. Эпюры перемещений.
Полное перемещение бруса вычисляется как сумма перемещений на предыдущих участках
7. Диаграммы растяжения и сжатия пластичных и хрупких материалов. Основные характеристики прочности и пластичности материалов. Наклёп.
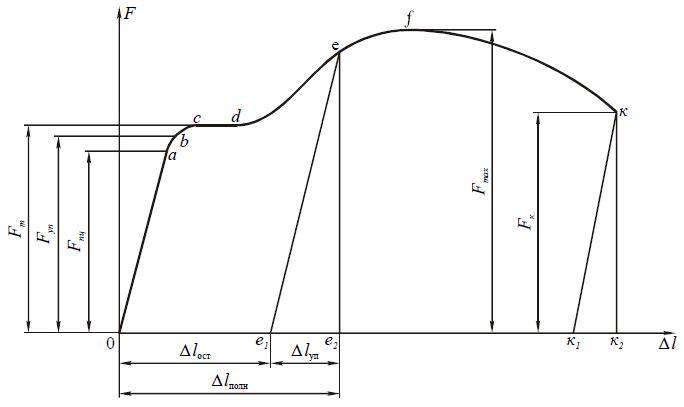
σпц=Fпц/A0 – предел пропорциональности;
σуп=Fуп/A0 – предел упругости;
σт=Fт/А0 – предел текучести;
σпр=Fmax/A0 – предел прочности при растяжении
А0- первоначальная площадь поперечного сечения. Начиная с точки d диаграммы деформация идет при дальнейшем увеличении нагрузки, происходит упрочнение металла. Упрочнение металла в результате прохождения пластической деформации называется наклёпом.
8. Методы расчёта по допускаемым напряжениям, разрушающим нагрузкам и предельным состояниям. Технико-экономические факторы влияющие на величину коэффициента запаса прочности.
По допускаемым
напряжениям:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
[σ]=σ0/n; [σ]=σт/nт(текучести); [σ]в=σв/nв(прочность при разрушении хруп.ких мат)
По предельным
состояниям:
![]() ;
;
![]() ;
;
![]() ;
;
По разрушающим
нагрузкам:
![]() ;
;
σ0 - напряжение соответствующее наступлению опасного состояния; n-коэф. запаса проч.
nт=1,4-1,6(пластичные материалы) nв=2,5-3,0(хрупкие материалы)
9. Основные виды задач в сопромате: определение напряжений, подбор сечений, определение допускаемой нагрузки по разным методам.(см. предыдущие вопросы)
По допускаемым
напряжениям:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
По предельным
состояниям:
![]() ;
;
![]() ;
;
![]() ;
;
По разрушающим
нагрузкам:
![]() ;
;
10. Статически неопределимые задачи при растяжении и сжатии. Учёт температуры и неточности изготовления. Определение предельных нагрузок.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
Задачи на стержни
1) Статическая сторона
Составить уравнения равновесия
2) Геометрическая сторона
Схема деформированного состояния
3) Физическая сторона
Выражаем деформации через внутренние усилия
4) Математическая сторона
Совместно решаем уравнения
5) Подбор сечения
Проверка по допускаемым напряжениям
Задачи на изменение температуры
![]()
9. Основные виды задач в сопромате: определение напряжений, подбор сечений, определение допускаемой нагрузки по разным методам.(см. предыдущие вопросы)
3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
1. Статические моменты. Определение центра тяжести плоской фигуры.
Статическим моментом сечения относительно данной оси называется сумма произведений элементарных площадей dA на их расстояния до данной оси (например, x или y), которая распространяется на всю площадь сечения A.
Статические моменты
инерции плоской фигуры:
![]()
![]()
![]()
![]()
Оси, проходящие через центр тяжести, называются центральными осями инерции.
Центр тяжести – это точка, обладающая свойством, что относительно любой оси проведённой через эту точку, статический момент равен 0.
Определение положения
центра тяжести:
![]()
![]()
