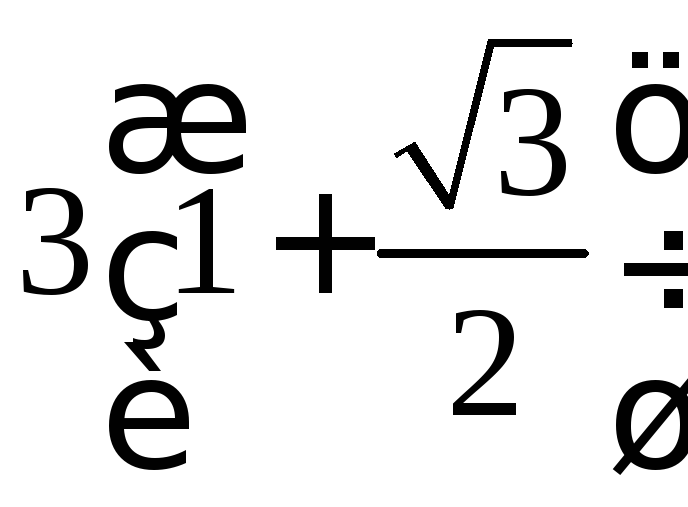- •1. Полярная система координат
- •1.1. Прямоугольная система координат на плоскости
- •1.2. Полярные координаты точек на плоскости
- •1.3. Связь между прямоугольными декартовыми и полярными координатами точек на плоскости
- •2. Некоторые линии в полярной системе координат и
- •2.1. Окружность
- •2.2. Спираль Архимеда
- •2.3. Розы
- •2.4. Кардиоида
- •2.5. Лемниската Бернулли
- •2.6. Правило построения кривых в полярной системе координат
- •3. Задания для самостоятельной работы
- •3.1. Варианты типового расчета «Полярная система координат»
- •3.2. Примеры выполнения заданий типового расчета
3.2. Примеры выполнения заданий типового расчета
З
а д а н и е 1. Заданы координаты точек
![]() в полярной системе координат:
в полярной системе координат:![]() :
1) построить точки в ПСК; 2) найти координаты
данных точек в ДПСК.
:
1) построить точки в ПСК; 2) найти координаты
данных точек в ДПСК.
Решение.
1) Сначала надо задать ПСК, используя определение 4. Для этого необходимо произвести следующее:
– отметить на плоскости точку О – начало координат (полюс);
– провести через точку О луч ОР (полярная ось);
– от полюса в направлении полярной оси отложить произвольной длины отрезок (принять его за единицу масштаба).
Чтобы
изобразить в заданной ПСК точку ![]() ,проводим
через полюс О
луч
,проводим
через полюс О
луч ![]() (полуось) под углом
(полуось) под углом ![]() к
полярной оси ОР
(или повернем полярную ось на угол
к
полярной оси ОР
(или повернем полярную ось на угол ![]() вокруг
точки О против часовой стрелки –
замечание
2, подразд. 1.2). Затем отложим на полученном
луче от точки О
отрезок
вокруг
точки О против часовой стрелки –
замечание
2, подразд. 1.2). Затем отложим на полученном
луче от точки О
отрезок
![]() длиной
длиной
![]() (две единицы выбранного масштаба). Его
конец – искомая точка.
(две единицы выбранного масштаба). Его
конец – искомая точка.
Для
построения точки ![]() надо
провести луч
надо
провести луч ![]() под
углом
под
углом ![]() к
полярной оси ОР
(или повернуть полярную ось на угол
к
полярной оси ОР
(или повернуть полярную ось на угол ![]() вокруг
точки О
по часовой стрелке) и отложить на нем
от точки О
отрезок
вокруг
точки О
по часовой стрелке) и отложить на нем
от точки О
отрезок
![]() длиной
длиной
![]() (три
единицы масштаба). Его конец – точка
(три
единицы масштаба). Его конец – точка![]() .
.
Для
построения точки
![]() нужно
провести луч
нужно
провести луч
![]() ,
составляющий с полярной осью угол
,
составляющий с полярной осью угол
![]() или,
что то же,
или,
что то же,
![]() –
главное
значение угла (замечание 3, подразд. 1.2)
и отложить на нем от полюса 3/2 единицы
масштаба. Все три заданные точки построены
на рис. 10.
–
главное
значение угла (замечание 3, подразд. 1.2)
и отложить на нем от полюса 3/2 единицы
масштаба. Все три заданные точки построены
на рис. 10.
2)
Выполним вторую часть задания. Найдем
прямоугольные декартовы координаты
точек. Необходимо воспользоваться
формулами (1). Подставляя вместо
![]() координаты точки
координаты точки![]() получим:
получим:

Итак,
в ДПСК координаты точки
![]()
![]() .
Аналогично получим координаты точек
.
Аналогично получим координаты точек![]() (рис.11).
(рис.11).
|
|
|

 Если совместить изображенные в
ДПСК и ПСК точки
так, чтобы начало координат ДПСК совпало
с полюсом ПСК, а направление полярной
оси ОР
– с направлением оси Ох,
то отмеченные точки должны совпасть.
Если совместить изображенные в
ДПСК и ПСК точки
так, чтобы начало координат ДПСК совпало
с полюсом ПСК, а направление полярной
оси ОР
– с направлением оси Ох,
то отмеченные точки должны совпасть.
З
а д а н и е 2. Заданы
координаты точек
![]() в ДПСК:
в ДПСК:![]()
![]() .
1) Найти полярные координаты данных
точек; 2) построить точки в ПСК и ДПСК,
совместив эти системы координат.
.
1) Найти полярные координаты данных
точек; 2) построить точки в ПСК и ДПСК,
совместив эти системы координат.
Решение.
1) Для нахождения полярных координат заданных точек воспользуемся формулами (2) и (3).
Для
точки ![]() имеем:
имеем:![]()
![]() ,тогда
,тогда
![]() .Так
как
.Так
как ![]() ,то
,то
![]()
![]() .Таким
образом, в ПСК
.Таким
образом, в ПСК
![]()
![]() .
.
Д ля
точки
ля
точки![]() имеем:
имеем:![]() ,тогда
,тогда
![]()
![]() .Так
как
.Так
как ![]() ,то
,то
![]()
![]()
![]()
![]() Таким образом, в ПСК
Таким образом, в ПСК![]()
![]()
Для
точки ![]() :
:![]()
![]() .Так
как
.Так
как ![]() ,то
,то
![]() .Итак,
в ПСК
.Итак,
в ПСК
![]()
![]()
2) Совместим ПСК с ДПСК и построим точки с заданными и полученными координатами (рис.12). Построение точек в ПСК рассмотрено в задании 1.
З
а д а н и е 3. Даны уравнения кривых в
ДПСК:
![]() .
Получить уравнения кривых в ПСК и
построить в ПСК: а)
.
Получить уравнения кривых в ПСК и
построить в ПСК: а)![]() ;б)
;б)
![]()
Решение.
а)
Определим тип кривой: ![]() –
это
окружность с центром в начале координат
и радиусом
–
это
окружность с центром в начале координат
и радиусом ![]() (см.
табл. 1).В
ПСК уравнение примет вид:
(см.
табл. 1).В
ПСК уравнение примет вид:![]()
![]() ,
так как
,
так как![]() При
любом значении полярного угла
При
любом значении полярного угла
![]() полярный радиус
полярный радиус
![]() постоянный и равен
постоянный и равен![]() (рис.13).
(рис.13).
б )Определим
тип кривой:
)Определим
тип кривой: ![]() –
это
окружность со смещенным центром (см.
табл. 1). Выделяя квадрат в левой части
равенства, получим каноническое
уравнение:
–
это
окружность со смещенным центром (см.
табл. 1). Выделяя квадрат в левой части
равенства, получим каноническое
уравнение:
![]() ;
;![]() .Координаты
центра
О
(0;
−3),
радиус R
= 3. Формулы (2) позволяют найти уравнение
этой окружности в ПСК:
.Координаты
центра
О
(0;
−3),
радиус R
= 3. Формулы (2) позволяют найти уравнение
этой окружности в ПСК:
![]()
![]()
![]() .
Это уравнение распадается на два:
.
Это уравнение распадается на два:![]() и
и![]() .
Первое уравнение при любом
.
Первое уравнение при любом
![]() представляет
полюс
– точку О.
Второе уравнение
представляет
полюс
– точку О.
Второе уравнение
![]() дает все точки окружности (в том числе
полюс), поэтому первое уравнение можно
опустить. Строим кривую
дает все точки окружности (в том числе
полюс), поэтому первое уравнение можно
опустить. Строим кривую![]() в ПСК.
в ПСК.
Воспользуемся правилом построения кривых в ПСК (подразд. 2.6).
Решаем неравенство:
 воспользуемся
данными табл. 5:
воспользуемся
данными табл. 5:

Выбираем значения полярного угла из промежутка
 :
при
:
при

 .
.Составим таблицу значений
 и
и :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
|
|
6 |
|
|
3 |
0 |
Строим точки с найденными координатами
 Построение точек в ПСК было рассмотрено
в задании 1.
Построение точек в ПСК было рассмотрено
в задании 1.Соединим точки плавной линией, получим изображение окружности радиусом R = 3 (рис.14).

З
а д а н и е 4. Даны уравнения кривых в
ПСК:![]() Построить кривую в ПСК и получить ее
уравнение в ДПСК:
а)
Построить кривую в ПСК и получить ее
уравнение в ДПСК:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение.
а)
Определим
тип кривой:
![]() – спираль Архимеда (подразд. 2.2).
– спираль Архимеда (подразд. 2.2).
Воспользуемся правилом построения кривых в ПСК (подразд. 2.6).
1.
Найдем пределы изменения полярного
угла, решая неравенство
![]() .
Тогда
.
Тогда![]()
2.
Выберем главное значение угла
![]() .
Поскольку
.
Поскольку![]() –
функция
не периодическая, то
–
функция
не периодическая, то
![]() ,
с учетом
,
с учетом![]() имеем
имеем![]()
3.
Составим таблицу значений
![]() и
и![]() Будем придавать значения полярному
углу
Будем придавать значения полярному
углу![]() через промежуток
через промежуток![]() (выбран произвольно).
(выбран произвольно).
Например,
при
![]() ;
;
при
![]() ;
;
при
![]() ;
;
при
![]() .
.
Полученные значения записываем в таблицу:
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
… |
4.
По таблице строим точки с найденными
полярными координатами
![]() :
:![]()
5. Соединим построенные точки плавной линией, получим изображение спирали Архимеда (рис.15).

Запишем
уравнение
![]() в ДПСК, используя формулы (2) и (3):
в ДПСК, используя формулы (2) и (3):
![]() .
.
б)
Определим
тип кривой:
![]() –
окружность со смещенным цент-ром и
радиусом R
= 4/2 = 2 (см.
табл. 1).
–
окружность со смещенным цент-ром и
радиусом R
= 4/2 = 2 (см.
табл. 1).
Воспользуемся правилом построения кривых в ПСК (подразд. 2.6).
Найдем пределы изменения полярного угла, решая неравенство
 .
Тогда
.
Тогда (см.
табл. 5)
(см.
табл. 5)Функция
 периодическая. Таким образом,
выберем значения углов из промежутка
периодическая. Таким образом,
выберем значения углов из промежутка
 при
при

Составим таблицу значений
 и
и
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
4 |
|
|
2 |
0 |
Строим точки с найденными координатами

Соединим точки плавной линией, получим изображение окружности радиусом R = 2 (рис.16).
Замечание:
построение графика
![]() можно провести другим способом. Так как
можно провести другим способом. Так как![]() функция четная, т. е.
функция четная, т. е.![]() ,
при построении достаточно ограничиваться
значениями
,
при построении достаточно ограничиваться
значениями
![]() ,
а затем отобразить г
,
а затем отобразить г рафик
симметрично относительно полярной оси
для углов
рафик
симметрично относительно полярной оси
для углов![]() .
.
Составим
уравнение данной окружности в ДПСК. В
силу формул (2) имеем:
![]()
![]() Приведем
полученное уравнение к каноническому
виду:
Приведем
полученное уравнение к каноническому
виду: ![]()
![]()
![]() –
окружность
со смещенным вдоль оси Ох
центром
(2; 0) и радиусом 2.
–
окружность
со смещенным вдоль оси Ох
центром
(2; 0) и радиусом 2.
в)
Определим
тип кривой:
![]() –
кардиоида (подразд. 2.3).
–
кардиоида (подразд. 2.3).
Строим заданную кривую.
1.
Найдем пределы изменения полярного
угла, решая неравенство
![]() .
Тогда
.
Тогда![]() ,
,![]() (см. табл. 5).
(см. табл. 5).
2.
Функция![]() периодическая.Выберем
значения полярных углов, т. е.
периодическая.Выберем
значения полярных углов, т. е.
![]() или
или![]() Удобнее взять промежуток
Удобнее взять промежуток![]()
3.
Составим таблицу значений
![]() и
и![]()
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
1,5 |
|
4,5 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
4,5 |
3 |
1,5 |
|
|
0 |
При
вычислении значений
![]() мы пользовались формулами приведения:
мы пользовались формулами приведения:
 .
Например:
.
Например: 

 и
т. д.
и
т. д.
Можно
вычислять значения
![]() на калькуляторе.
на калькуляторе.
4.
Строим
точки с найденными координатами
![]()
5. Соединим точки плавной линией, получим кардиоиду (рис.17).
Замечание:
построение графика
![]() можно провести другим способом. Так как
можно провести другим способом. Так как![]() функция четная, т. е.
функция четная, т. е.![]() ,
при построении достаточно ограничиваться
значениями
,
при построении достаточно ограничиваться
значениями
![]() а затем отобразить график симметрично
относительно полярной оси для углов
а затем отобразить график симметрично
относительно полярной оси для углов![]()
При
переходе к ДПСК уравнение кардиоиды
![]() примет
вид:
примет
вид:

 умножим обе части ра-венства на
умножим обе части ра-венства на ![]() получим
получим![]()
![]() или
или
![]() .
.

З
а д а н и е 5. Даны уравнения кривых в ДПСК
и ПСК. Построить кривые в ПСК: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
Решение.
а)
Определим
тип кривой:
![]() −лемниската
Бернулли (подразд. 2.5). Воспользуемся
формулами (2), связывающими декартовы
координаты с полярными координатами.
Тогда уравнение заданной кривой можно
записать в виде:
−лемниската
Бернулли (подразд. 2.5). Воспользуемся
формулами (2), связывающими декартовы
координаты с полярными координатами.
Тогда уравнение заданной кривой можно
записать в виде:
![]() или
или![]() .
.![]() ,
,![]() .
Это
уравнение распадается на два:
.
Это
уравнение распадается на два:![]() и
и![]() .Первое
уравнение при любом
.Первое
уравнение при любом
![]() представляет
полюс
– точку О.
Второе уравнение:
представляет
полюс
– точку О.
Второе уравнение: ![]() дает все точки кардиоиды (в том числе
полюс), поэтому первое уравнение можно
опустить.
Используя
формулу
дает все точки кардиоиды (в том числе
полюс), поэтому первое уравнение можно
опустить.
Используя
формулу
![]() ,
получим:
,
получим:![]() ,
,![]() или
или
![]() .
Т.
к.
.
Т.
к. ![]() .
Построим кривую, заданную уравнением:
.
Построим кривую, заданную уравнением:
![]() .
Воспользуемся
правилом построения кривых в ПСК
(подразд. 2.6).
.
Воспользуемся
правилом построения кривых в ПСК
(подразд. 2.6).
1.
Функция определена при
![]() ,
что равносильно неравенству (см. табл.
5)
,
что равносильно неравенству (см. табл.
5)
![]() или
или![]()
2. Выбираем значения полярного угла:
при
![]() ,
при
,
при![]()
3.
Составим
таблицу значений
![]() и
и![]() ,
разбивая полученные в п. 2 отрезки на
отрезки длиной
,
разбивая полученные в п. 2 отрезки на
отрезки длиной![]()
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
0 |
|
1 |
|
0 |
4.
Строим точки с найденными координатами
![]()
5. Соединим точки последовательно плавной линией, получим лемнискату Бернулли (рис. 18).
Замечание: данную кривую можно построить другими способами.
1)
Поскольку
![]() − периодическая функция с периодом
− периодическая функция с периодом![]() ,
то достаточно построить часть кривой
при
,
то достаточно построить часть кривой
при
![]() ,
а другую половину лемнискаты получить
поворотом построенной части на угол
,
а другую половину лемнискаты получить
поворотом построенной части на угол![]()
 2)
Можно учесть и тот факт, что
2)
Можно учесть и тот факт, что
![]() − функция четная. Тогда при построении
достаточно ограничиться значениями
− функция четная. Тогда при построении
достаточно ограничиться значениями
![]() ,
а затем отобразить график симметрично
относительно прямой,перпендикулярной
полярной
оси для углов
,
а затем отобразить график симметрично
относительно прямой,перпендикулярной
полярной
оси для углов
![]() .
.
б)
Определим тип кривой:
![]() − «четырехлепестковая роза» (подразд.
2.3).
− «четырехлепестковая роза» (подразд.
2.3).
Строим данную кривую в ПСК.
1.
Решаем неравенство ![]() или
или
![]() (см.
табл. 5),
(см.
табл. 5),![]()
![]()
2.
Выбираем значения
полярного угла:
при ![]()
![]() ,
при
,
при ![]()
![]() ,
при
,
при![]()
![]() ,
при
,
при![]()
![]()
3.Составим
таблицу значений
![]() и
и![]() :
:
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
3/2 |
3/4 |
0 |
0 |
3/4 |
|
|
|
|
|
|
|
|
|
|
|
3/2 |
3/4 |
0 |
0 |
3/4 |
3/2 |
3/4 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
3/4 |
3/2 |
3/4 |
0 |
4.
Строим точки с найденными координатами
![]()
5. Соединим точки плавной линией, получим изображение кривой «четырехлепестковая роза» (рис.19).

в)
Определим
тип кривой:
![]() − «трехлепестковая роза» (подразд.
2.3).
− «трехлепестковая роза» (подразд.
2.3).
Строим данную кривую в ПСК.
1.
Решаем неравенство ![]() или
или
![]() (см.
табл.5):
(см.
табл.5):![]()
![]()
2.
Выбираем значения
полярного угла
![]() при
при![]()
![]() ,
при
,
при
![]() при
при ![]() .
.
3.
Разбивая полученные отрезки на отрезки
длиной
![]() ,
составим таблицу значений
,
составим таблицу значений![]() и
и![]() :
:
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
4 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
0 |
0 |
|
4 |
|
0 |
4.
Строим точки с найденными координатами
![]()
5. Соединим точки плавной линией, получим изображение кривой «трехлепестковая роза» (рис. 20).
г)
Определим
тип кривой:
![]() − «двухлепестковая роза».
− «двухлепестковая роза».
Строим данную кривую в ПСК.
1.
Решаем неравенство ![]() или
или
![]() (см.
табл.5):
(см.
табл.5): ![]()
![]()
2.
Выбираем значения
полярного угла из промежутка![]() :
при
:
при ![]() ,
при
,
при ![]()
3.
Составим
таблицу значений
![]() и
и![]() :
:
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
2 |
|
0 |
0 |
|
2 |
|
0 |
4.
Строим точки с найденными координатами
![]()
5 .
Соединим точки плавной линией, получим
изображение кривой«двухлепестковая
роза»
(рис. 21).
.
Соединим точки плавной линией, получим
изображение кривой«двухлепестковая
роза»
(рис. 21).
Библиографический список
1. В ы г о д с к и й М. Я. Справочник по высшей математике / М. Я. В ы -г о д с к и й. М.: Астрель, 2006. 991 с.
2. Ефимов Н. В. Краткий курс аналитической геометрии. 13-е изд. / Н. В. Ефимов. М.: Физматлит, 2004. 496 с.
3. Н а т а н с о н И. П. Краткий курс высшей математики. 10-е изд. / И. П. Н а т а н с о н. СПб: Лань, 2009. 727с
4. П и с ь м е н н ы й Д. Т. Конспект лекций по высшей математике /
Д. Т. П и с ь м е н н ы й. М.: Айрис-Пресс, 2006. Ч. 1. 288 с.
5. П р и в а л о в И. И. Аналитическая геометрия. 38-е изд. / И. И. П р и- в а л о в. СПб: Лань, 2010. 299 с.