1. Полярная система координат

1.1. Прямоугольная система координат на плоскости

О п р е д е л е н и е 1. Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости.

Наиболее распространенной из систем является прямоугольная (декартова) система координат (ДПСК).

О п р е д е л е н и е 2. ДПСК на плоскости задается следующим образом:

1) точкой О – начало координат;

2) осями координат – две взаимно перпендикулярные прямые, пересекающиеся в точке О, на каждой из которых выбрано положительное направление;

3) единицей масштаба – единичной длины отрезок (рис.1).

Оси координат чаще всего располагают вертикально и горизонтально, при этом горизонтальную ось Ох, направленную слева направо, называют осью абсцисс, вертикальную ось Оу, направленную снизу вверх, называют осью ординат. Оси координат делят координатную плоскость на четыре области – четверти (квадранты). Единичный отрезок выбирают произвольно, одинаковым для обеих осей. Обозначают ДПСК – Оху.

О п р е д е л е н и е 3. Плоскость, в которой расположена система координат, называют координатной плоскостью.

Взяв произвольную точкуМ на координатной плоскости (см. рис. 1), найдем ее проекции P и Q на координатные оси Ох и Оу соответственно. Отрезок OP на оси абсцисс, а также число х, измеряющее его длину в выбранном масштабе, называют абсциссой точки М; отрезок OQ на оси ординат, а также измеряющее его число у – ординатой точки М. Величины х = OP, у = OQ называют прямоугольными координатами точки М и обозначают М (х; у).

Числа х и у полностью определяют положение точки на плоскости, а именно: каждой упорядоченной паре чисел х и у соответствует единственная точка М плоскости и, наоборот, каждой точке М плоскости соответствует одна пара чисел – х, у.

Прямоугольная система координат называется декартовой по имени французского философа и математика Рене Декарта (1596 – 1650).

1.2. Полярные координаты точек на плоскости

Кроме ДПСК существуют и другие системы координат, позволяющие определить положение точки на плоскости с помощью пары действительных чисел.

Рассмотрим систему координат, когда отношения между точками плоскости проще изобразить в виде радиусов и углов, такая система называется полярной системой координат (ПСК).

О п р е д е л е н и е 4. Полярная система координат на плоскости задается следующим образом:

1) точкой О, называемой полюсом;

2) лучом, исходящим из точки О, называемым полярной осью;

3) единицей масштаба – единичный отрезок произвольной длины (рис. 2).

О п р е д е л е н и е 5. Полярным радиусом любой точкиМ плоскости называется расстояние от полюса О до нее, т. е. длина отрезка ОМ (ОМ = ρ).

О п р е д е л е н и е 6. Полярным углом точкиМ называется угол наклона отрезка ОМ к полярной оси (т. е.).

О п р е д е л е н и е 7. Числа и(полярный радиус и полярный угол точкиМ) называются полярными координатами точки и обозначаются М.

Замечания

1. Полярный радиус 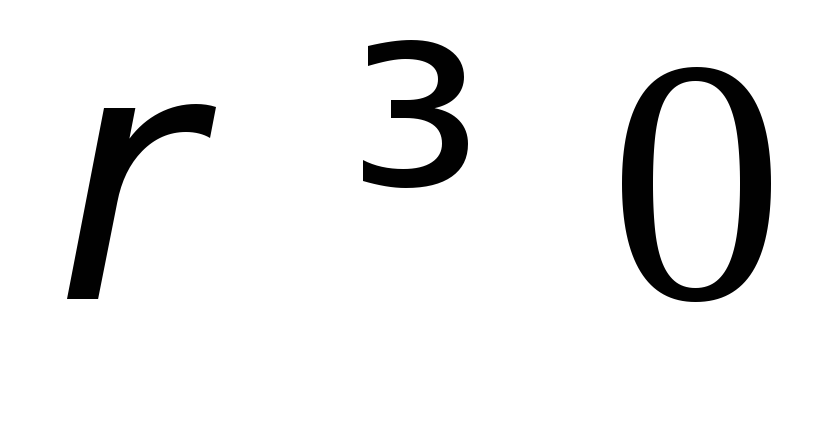, так как – расстояние, величина неотрицательная.

2. Е

   Рис.3

   сли полярный угол, то он откладывается против часовой стрелки, а если, то – по ходу часовой стрелки.

3. Так как точка плоскости при повороте ее вокруг полюса на 2π возвращается в прежнее положение, то измерение полярного угла можно рассматривать так: и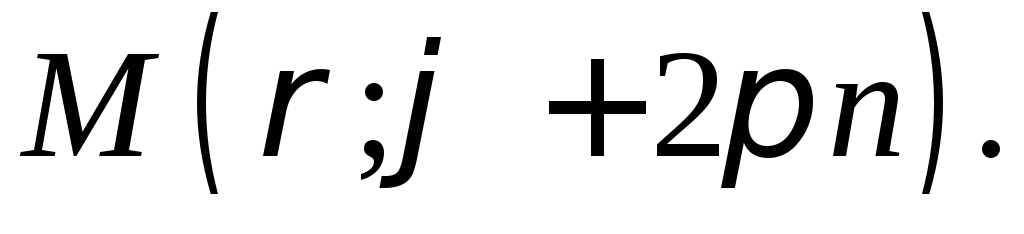Обычно в качестве полярных углов берут так называемые главные их значения, определяемые неравенствомили

4. Для точки О (полюса) 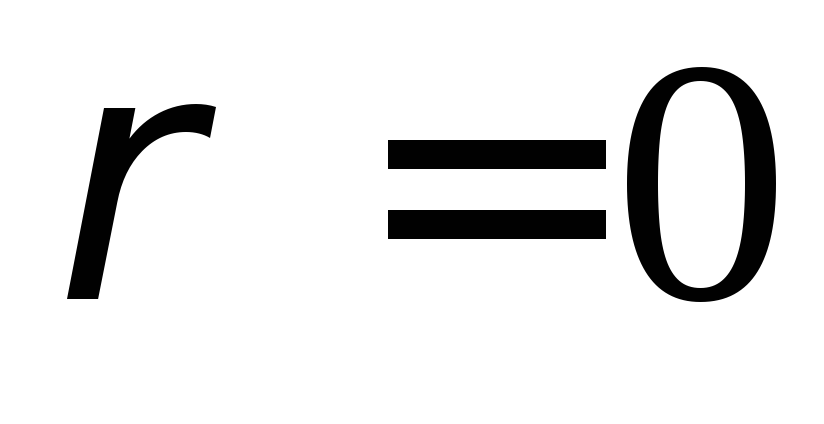, а угол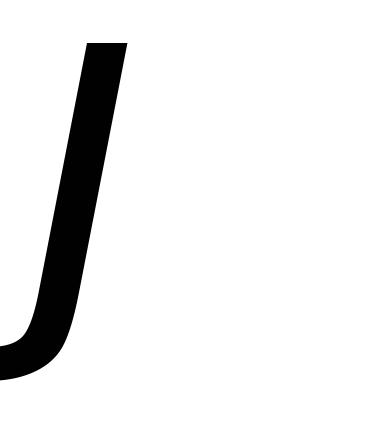произвольный. Если, то точкаМ совпадает с полюсом.

5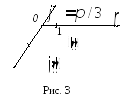. В некоторых источниках рассматривают и отрицательные значения полярного радиуса, понимая при этом под точкойточку. Уголхарактеризует направление полярного радиуса, прямо противоположное тому, которое соответствует углуТогда искомая точка изображается не на луче, образующем уголс полярной осью, а на продолжении этого луча в противоположном направлении на расстоянииот полюса. Например, точке будет соответствовать точка(рис. 3). Иными словами, ту же точку можно задать, пользуясь положительным значением Аналогичным образом, прибавив каргументу , можно превратить отрицательное в положительное. Имея это в виду, условимся считать

Д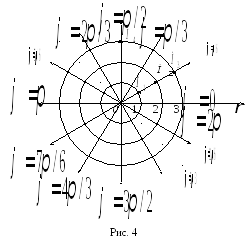ля изображения точек в ПСК произвольно разобьем ее лучами, исходящими из полюсаО, на секторы, образующие соответствующие углы с полярной осью. Проведем концентрические окружности с центром в точке О и с радиусами 1, 2, 3 (рис. 4). На рис. 4 изображены точки

.