
1_Краткий курс физики (часть 2)
.pdf
пружину, иотпустим. Возникающаяприрастяжениипружинысилаупругости
|
Fупр |
|
|
Fупр, x = −k x , |
(74) |
||
|
|
x |
будет стремиться вернуть грузик в положе- |
||||
|
0 |
xm |
ние равновесия, разгоняя его. Вернувшись |
||||
|
|
|
в положение равновесия, грузик продолжит |
||||
|
|
v =vm |
движение по инерции, сжимая пружину, |
||||
|
|
x |
пока под действием силы упругости не ос- |
||||
|
0 |
xm |
тановится в крайнем левом положении, по- |
||||
|
|
|
сле чего таким же образом вернется в ис- |
||||
|
|
Fупр |
ходное положение. |
|
|
||
|
|
x |
Уравнение движения грузика |
|
|||
-xm |
|
max = Fупр, x + Fтр, x |
(75) |
||||
0 |
xm |
||||||
после подстановки силы упругости и эле- |
|||||||
Рис. 14. |
|
||||||
|
|
|
ментарных |
преобразований |
приводит |
к |
|
дифференциальному уравнению собственных колебаний |
|
||||||
x + |
k |
x = 0, |
(76) |
|
m |
||||
|
|
|
где x – координата грузика (неизвестная функция времени), а корения грузика на ось Ox.
Решением этого уравнения будут функции вида x(t )= xm cos(ω0t +ϕ0 );
x(t )= xm sin (ω0t +ϕ0 ),
x – проекция ус-
(77)
где x |
m |
– амплитуда колебаний, ω = |
k |
– циклическая частота собственных |
|
||||
|
0 |
m |
|
|
|
|
|
|
колебаний.
Механическая энергия грузика, как известно из механики, складывается из его кинетической и потенциальной энергий
|
|
|
mv 2 |
|
kx2 |
|
mv |
2 |
kx2 |
|
W =W +W |
p |
= |
|
+ |
|
= |
|
m = |
m . |
(78) |
|
|
|
||||||||
k |
|
2 |
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
Теперь рассмотрим электромагнитные колебания, которые происходят в идеальном колебательном контуре – контуре, в котором активным сопротивлением можно пренебречь.
31

|
|
|
|
|
|
|
|
Запишем для колебательного контура вто- |
|||
|
|
|
С |
|
|
|
рое правило Кирхгофа |
|
|||
|
|
|
L |
|
|
UC =EL , |
(79) |
||||
|
|
|
|
|
|
|
которое с учетом определения электроемкости и |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
закона Фарадея-Ленца примет вид дифферен- |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
циального уравнения собственных колебаний в |
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
колебательном контуре |
|
||
|
|
|
|
|
Рис. 15. |
|
|||||
|
|
|
|
|
|
q + |
1 |
q = 0 , |
(80) |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
LC |
|
|
где q – заряд на обкладках конденсатора (неизвестная функция времени), q – вторая производная от заряда (не имеет специального названия).
Решением этого дифференциального уравнения будут гармонические функции косинуса и синуса
q(t)= qm cos(ω0t +ϕ0 ); (81) q(t)= qm sin (ω0t +ϕ0 ),
которые с точностью до обозначений совпадают с решением уравнения для собственных механических колебаний. Здесь qm – амплитуда колебаний заряда
на обкладках конденсатора, а ω0 = LC1 - циклическая частота собственных
колебаний в колебательном контуре.
Энергия колебаний в колебательном контуре складывается из энергии заряженного конденсатора и энергии тока в катушке
|
q2 |
|
Li |
2 |
q2 |
|
Li2 |
|
|
W =W +W = |
|
+ |
|
= |
m |
= |
m . |
(82) |
|
2C |
2 |
2C |
|||||||
Э М |
|
|
|
2 |
|
Любая система, в которой могут происходить гармонические колебания, называется гармоническим осциллятором. Примером гармонического осциллятора является пружинный маятник (грузик, закрепленный на пружине), математический маятник (материальная точка, подвешенная на длинной нерастяжимой нити), физический маятник (твердое тело, закрепленное на оси вращения, не проходящей через центр масс), колебательный контур (электрическая цепь, состоящая из конденсатора и катушки индуктивности). Уравнения, описывающие процессы, происходящие в различных осцилляторах, очень похожи между собой по форме, различаясь лишь входящими в них величинами
32

(буквами). Это позволяет записывать физические законы, характеризующие осцилляторы, с помощью так называемых обобщенных величин. Так, положения грузика, закрепленного на пружине, характеризуется его координатой x, отклонение математического и физического маятников от положения равновесия, описывается углом поворота α, а состояние колебательного контура полностью характеризуется зарядом q на обкладках конденсатора. Введем понятие обобщенной координаты ξ, которая будет общим обозначением для любой из названных величин, поскольку законы их изменения одинаковы.
Тогда дифференциальное уравнение собственных колебаний можно записать в общем виде
|
|
|
|
|
|
|
|
|
|
|
|
ξ +ω02ξ = 0 , |
(83) |
|||
где ξ |
|
– обобщенное ускорение (вторая производная от обобщенной координа- |
||||||||||||||
ты), |
ω |
0 |
|
- частота |
собственных |
колебаний осциллятора, равная ω = |
|
k |
, |
|||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
m |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ω |
0 |
= |
|
g |
, |
ω |
0 |
= mga |
и |
ω = |
1 |
для пружинного, математического, физиче- |
||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
I |
|
0 |
LC |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ского маятников и идеального колебательного контура соответственно. Решением дифференциального уравнения будут гармонические функции,
которые также можно записать в общем виде
ξ (t )=ξm cos(ω0t +ϕ0 ); (84)
ξ (t )=ξm sin (ω0t +ϕ0 ).
Сложение однонаправленных колебаний занимает в физике колебаний и волн особенное место, поскольку этот вопрос не только представляет интерес сам собой, но и лежит в основе таких волновых явлений как интерференция и дифракция волн. Сначала рассмотрим сложение двух однонаправленных колебаний одинаковых частот и амплитуд
x1 |
= xm cosωt |
(85) |
|
x2 = xm cos(ωt +ϕ0 ) |
|||
|
|||
Результирующее колебание x = x1 + x2 , которое можно получить как аналитически, так и методом векторных диаграмм
x = 2x cos ϕ0 |
cos |
|
ωt + |
ϕ0 |
|
, |
(86) |
|
m |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
амплитуда
33
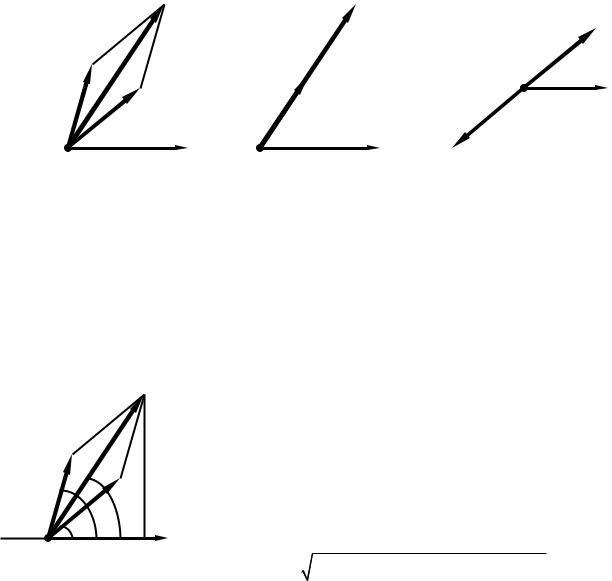
представляет собой гармоническое колебание такой же частоты, амплитуда которого зависит от разности фаз складываемых колебаний. Наибольший практический интерес представляют два частных случая ϕ0 = 0 и ϕ0 =π , при которых складываемые колебания максимально усиливают друг друга и максимально
а) |
|
2x cos ϕ0 |
б) |
2xm |
в) |
|||||
|
|
|
m |
2 |
|
|
|
xm (рез) = 0 |
||
|
|
|
|
|
|
|
|
|||
|
|
xm (2) |
|
|
|
|
|
xm (1) |
||
|
|
|
xm (2) |
|
|
|
x |
|||
|
|
|
|
|
xm (1) |
|
|
|||
|
|
|
xm (1) |
|
|
xm (2) |
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
x |
|
||
Рис. 16.
гасят друг друга соответственно. Векторные диаграммы, нарисованные для произвольной разности фаз складываемых колебаний, а также для описанных двух частных случаев, представлены на рисунке 16.
В общем случае, при сложении двух однонаправленных колебаний произвольных амплитуд, частот и начальных фаз
xm2
xm1
ϕ1 ϕ2 ϕ
x
Рис. 17.
|
x1 = xm1 cos(ω1t +ϕ01 ) |
|
||
xm |
|
ϕ1 |
(87) |
|
x2 |
= xm2 cos(ω2t +ϕ02 ) |
|||
|
|
|||
|
|
ϕ2 |
|
|
методом векторных диаграмм (см. рисунок 17) амплитуду и фазу результирующего колебания получим из теоремы косинусов и определения тангенса угла соответственно
x = |
x2 |
|
+ x2 |
+ 2x |
x |
|
cos |
(ϕ |
2 |
−ϕ ) |
|||
m |
m1 |
|
m2 |
|
m1 m2 |
|
|
|
|
1 |
|||
ϕ = arctg |
|
xm1 sinϕ1 + xm2 sinϕ2 |
|
|
(88) |
||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
x |
cosϕ + x |
cosϕ |
2 |
|
|
|
|||||
|
|
|
m1 |
|
1 |
m2 |
|
|
|
|
|
|
|
Сложение двух взаимно перпендикулярных колебаний можно наблюдать, если частица участвует одновременно в двух колебаниях, происходящих во взаимно перпендикулярных направлениях. В общем случае, такие колебания можно описать законами движения
34

x(t)= xm cos(ω1t +ϕ01 ) |
, |
(89) |
y(t)= ym cos(ω2t +ϕ02 ) |
которые, как известно из курса механики, представляют собой уравнение траектории в параметрической форме. Если частоты складываемых колебаний кратные, то траектория будет замкнутой кривой, вдоль которой колеблющаяся частица будет проходить многократно, в противном случае траектория будет сложной незамкнутой линией. Замкнутые траектории, возникающие при сложении двух взаимно перпендикулярных колебаний, называются фигурами Лиссажу. Чтобы получить уравнение траектории в явном виде, необходимо в приведенных выше функциях избавиться от времени как от параметра. Действия, которые при этом необходимо проделать, зависят от конкретного вида исходных функций, описывающих складываемые колебания.
Для примера рассмотрим сложение двух колебаний, происходящих с одинаковыми частотами (без нарушения общности начальную фазу одного из них можно выбрать равной нулю):
x = xm cosωt |
(90) |
|
y = ym cos(ωt +ϕ0 ). |
||
|
Выразим косинус из первой формулы и подставим во вторую, предварительно расписав в ней косинус суммы углов. После элементарных преобразований, получим формулу
|
x2 |
+ |
|
y2 |
−2 |
x |
|
y |
cosϕ |
0 |
=sin |
2 |
ϕ |
0 |
, |
(91) |
|||||||||
|
x2 |
|
y2 |
x |
y |
m |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
m |
|
|
|
m |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
которая для трех частных случаев |
|
ϕ0 = 0, ϕ0 =π, ϕ0 =π 2, |
приводит к трем |
||||||||||||||||||||||
уравнениям траектории соответственно |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y = |
y |
m |
x, |
y = − |
|
|
y |
m |
|
x, |
x2 |
|
+ |
y2 |
|
=1. |
|
(92) |
|||||||
x |
|
|
x |
|
|
x2 |
|
|
y2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
m |
|
|
|
|
|
m |
|
m |
|
m |
|
|
|
|
|
||||||||
Графикиэтихфункцийприведенынарис. 18 (дляопределенностивыбрано ym > xm ). Наиболее наглядно фигуры Лиссажу получаются на экране осциллографа, если электрические колебания подать на взаимно перпендикулярные отклоняющие пластины осциллографа. При других соотношениях частот и разности
фаз складываемых колебаний фигуры Лиссажу имеют более сложный вид.
35

|
ymB B |
ymB B |
ymB B |
|
||
ϕ0 = 0 |
|
ϕ0 =π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xm |
|
xm |
ϕ0 |
=π 2 |
xm |
|
|
|
|
|||
|
|
|
|
|||
Рис. 18.
Затухающие колебания, в отличие от собственных, возможных лишь в идеальных системах, происходят в реальных физических системах, в которых практически всегда присутствует трение (сопротивление). Действительно, маятник, выведенный из положения равновесия, будет совершать колебания лишь некоторое время, в течение которого амплитуда колебаний будет постоянно уменьшаться, пока движение маятника не прекратится вовсе.
Рассмотрим затухающие механические колебания на примере грузика, закрепленного на пружине (рис. 19). Выведем грузик из положения равновесия, растянув пружину, и отпустим. При движении грузика на него, кроме силы упругости
Fупр |
Fтр |
|
|
|
x |
0 |
xm |
Рис. 19. |
|
Fупр, x = −k x , |
(93) |
будет действовать сила вязкого трения (например, со стороны воздуха), которую можно считать пропорциональной скорости
Fтр, x = −μvx |
(94) |
Уравнение движения грузика под действием названных сил |
|
max = Fупр, x + Fтр, x |
(95) |
после подстановки сил упругости и трения и элементарных преобразований приводиткдифференциальному уравнению затухающих колебаний
x + 2 |
μ |
x + |
k |
x = 0 , |
(96) |
|
2m |
m |
|||||
|
|
|
|
где x – координата грузика (неизвестная функция времени), а x , x - проекции скорости и ускорения грузика соответственно.
Решением этого уравнения будут функции вида
36

|
|
|
x(t)= x |
e−βt cos(ωt +ϕ |
0 |
); |
|||
|
|
|
m0 |
|
|
|
(97) |
||
|
|
|
x(t)= x |
e−βt sin (ωt +ϕ |
|
|
|
||
|
|
|
0 |
), |
|||||
|
|
|
m0 |
|
|
|
|||
где |
x |
|
- начальная амплитуда колебаний, β = |
μ |
|
|
|
– коэффициент затухания, |
|
|
|
|
|
|
|||||
|
m0 |
|
|
|
2m |
|
|||
|
|
|
|
|
|
||||
ω = |
ω |
2 |
− β2 – частота затухающих колебаний, а множитель, стоящий перед |
||||||
|
0 |
|
|
|
|
|
|
|
|
косинусом или синусом xm (t)= xm0e−βt , является убывающей с течением вре-
мени амплитудой колебаний.
Электромагнитные затухающие колебания происходят в колебательном контуре, в котором нельзя пренебречь активным сопротивлени-
ем контура R. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Запишем |
для |
колебательного |
контура |
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
С |
|
|
|
второе правило Кирхгофа |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
L |
|
|
|
UC +UR =EL , |
(98) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
которое с учетом определения электроемкости, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
R |
|
|
|
закона Ома и закона Фарадея-Ленца примет вид |
||||||
|
|
|
|
|
|
|
|
|
|
|
дифференциального уравнения затухающих ко- |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
лебаний в колебательном контуре |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 20. |
|
|
|
|
R |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
q + 2 |
|
q + |
|
q = 0, |
(99) |
|
|
|
|
|
|
|
|
|
|
|
2L |
LC |
||||
где q – заряд на обкладках конденсатора (неизвестная функция времени), q – сила тока, q – производная от силы тока (не имеет специального названия).
Решением этого дифференциального уравнения будут гармонические функции косинуса и синуса
q(t )= q |
e−βt cos(ωt +ϕ |
0 |
); |
|
m0 |
|
|
(100) |
|
q(t )= q |
e−βt sin (ωt +ϕ |
|
|
|
0 |
), |
|||
m0 |
|
|
||
которые с точностью до обозначений совпадают с решением уравнений для ме-
ханических затухающих колебаний. Здесь коэффициент затухания β = 2RL .
В общем виде дифференциальное уравнение затухающих колебаний имеет вид
ξ + 2βξ +ω02ξ = 0 , |
(101) |
решением которогобудутфункциикосинусаилисинусаспеременнойамплитудой
37

|
ξ (t)=ξm0e−βt cos(ωt +ϕ0 ); |
|
|
|
|
(102) |
|
|
ξ (t)=ξm0e−βt sin (ωt +ϕ0 ), |
|
|
|
График |
первой из |
них |
|
представлен на рисунке 21. |
|
|
ξ, см |
Кроме |
коэффициента |
за- |
тухания и частоты затухающих |
|||
t, c |
колебаний, затухающие коле- |
||
|
бания также принято характе- |
||
|
ризовать временем релаксации τ |
||
и логарифмическим декрементом затухания Λ. Време-
нем релаксации называется промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в e раз ( e = 2,71... - основание натуральных логарифмов). Время релаксации связано с коэффициентом затуха-
ния простой формулой τ = β1 .
Логарифмическим декрементом затухания называется безразмерная скалярная физическая величина, равная натуральному логарифму отношения соседних амплитуд, то есть
Λ = ln |
ξm (t ) |
(103) |
|
ξm (t +T ) |
|
||
Вынужденными колебаниями называются колебания, |
возни- |
||
кающие в системе под действием внешней периодической силы. |
|
||
Пусть теперь на грузик, закрепленный на пружинке, кроме сил упругости |
|||
и трения, действует внешняя сила, меняющаяся со временем по закону |
|
||
Fx (t)= Fm cosωt , |
(104) |
||
то уравнение движения примет вид |
|
||
max = Fупр, x + Fтр, x + Fm cosωt . |
(105) |
||
После подстановки сил упругости и трения и элементарных преобразований получим дифференциальное уравнение вынужденных колебаний
x + 2 |
μ |
x + |
k |
x = |
Fm |
cosωt , |
(106) |
2m |
m |
|
|||||
|
|
|
m |
|
|||
решением которого являются гармонические функции косинуса или синуса. 38

Второе правило Кирхгофа, записанное для так называемого последовательного колебательного контура, в котором в разрыв цепи контура включена внешняя переменная электродвижущая сила
E (t)=Em cosωt , |
(107) |
имеет вид |
|
UC +UR =EL +Em cosωt . |
(108) |
С учетом определения электроемкости, закона Ома и закона Фарадея-Ленца получим дифференциальное уравнение вынужденных колебаний в последовательном колебательном контуре
q + 2 |
R |
q + |
1 |
q = Em cosωt , |
(109) |
|
2L |
LC |
|||||
|
|
L |
|
которое с точностью до обозначений совпадает с дифференциальным уравнением колебаний грузика на пружине, что позволяет записать уравнение вынужденных колебаний в общем виде
ξ + 2βξ +ω02ξ =αm cosωt , |
(110) |
где αm = Fm  m для грузика на пружине и αm =Em
m для грузика на пружине и αm =Em  L для колебательного контура. Решением этого дифференциального уравнения будут гармонические
L для колебательного контура. Решением этого дифференциального уравнения будут гармонические
функции
ξ (t)=ξm cos(ωt −ϕ0 ); (111)
ξ (t)=ξm sin (ωt −ϕ0 ).
Видно, что вынужденные колебания происходят с частотой внешней силы, а амплитуда и начальная фаза вынужденных колебаний могут быть найдены аналитически или методом векторных диаграмм и определяются формулами
ξm = |
αm |
|
; |
(ω2 −ω02 )2 |
|
||
|
+ 4β2ω2 |
||
|
|
(112) |
|
ϕ0 = arctg ω22 βω−ω2 , 0 <ϕ0 <π.
0
Видно, что амплитуда и начальная фаза зависят от коэффициента затухания осциллятора и соотношения частоты внешней силы и частоты собственных колебаний осциллятора.
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешней силы к частоте собственных колебаний осциллятора.
39

Добротностью называется безразмерная скалярная физическая величина, равная умноженному на 2π отношению энергии, запасенной в осцилляторе, к ее диссипации за один период колебаний при частоте колебаний, равной собственной, то есть
Q = 2π |
W |
. |
(113) |
|
|||
|
W |
|
|
|
дис |
|
|
Добротностью также называется безразмерная скалярная физическая величина, характеризующая высоту резонансного пика и равная отношению амплитуды вынужденных колебаний при собственной частоте к амплитуде колебаний при частоте внешней вынуждающей силы, стремящейся к нулю, то есть
Q = |
ξm (ω =ω0 ) |
|
ξm (ω = 0) . |
(114) |
Во всех случаях формулы, определяющие добротность, сводятся к выражению
Q = 2ωβ0 , а при малом затухании в осцилляторе (β <<ω0 ), то есть при Q >>1,
добротность окажется обратно пропорциональной логарифмическому декре-
менту затухания Q = πΛ .
8. УПРУГИЕ И ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
При определенных условиях колебания обладают способностью распространяться в пространстве. Такие распространяющиеся в пространстве и взаимосвязанные колебания называются волнами. Волны бывают различных видов: упругие, поверхностные, электромагнитные и т. д. Смещения частиц от положения равновесия (колебания) в волне могут быть сориентированы как вдоль линии распространения волны (такие волны называются продольными), так и в плоскости, перпендикулярной направлению распространения волны (такие волны называются поперечными). Упругие волны могут иметь все возможные поляризации (могут быть и продольными, и поперечными в зависимости от свойств среды, в которой они распространяются), а электромагнитные волны (распространяющиеся в пространстве колебания электрического и магнитного полей) существуют только поперечные. Все виды волн распространяются в пространстве с конечной, но вполне определенной для данных условий скоростью v (скорость электромагнитных волн в вакууме – скорость света – обозначается с).
40
