3126 Моделирование контрольная

const n=18; numax= 50; nvmax=100; intmax=32767; type

ta=array[0..n+1,0..n+1] of integer; tu=array[0..numax] of integer; tv=array[0..nvmax] of integer;

var

Form1: TForm1; su,nuway,nvway,ushort:tu; nv,nu,k,kushort:integer;

implementation

{$R *.dfm}

procedure TForm1.BitBtn1Click(Sender: TObject); type Tmatr=array[1..18,1..3]of integer;

const TestMatr:Tmatr=((1,2,8),(2,6,3),(2,3,3),(3,4,1),(4,8,4), (5,9,3),(5,6,3),(6,7,1),(7,11,4),(7,8,2),(8,12,3),(9,10,1), (10,11,2),(11,14,3),12,15,3),(12,13,3),(14,15,3),(15,16,5)); var n:integer;

begin

for n:=1 to 18 do begin

StringGrid1.Cells[0,n]:=Inttostr(n);

StringGrid1.Cells[1,n]:=Inttostr(testmatr[n,1]);

StringGrid1.Cells[2,n]:=Inttostr(testmatr[n,2]);

StringGrid1.Cells[3,n]:=Inttostr(testmatr[n,3]);

end;

end;

procedure TForm1.BitBtn2Click(Sender: TObject); var i,j,k,nut,nvt,sunew:integer;

break1,zeitnot:boolean; begin

su[1]:=0; zeitnot:=false; nv:=StrToInt(Edit1.Text); nu:=StrToInt(Edit2.Text); Proverka(Sender);

for nut:=1 to nu do nuway[nut]:=intmax; for nut:=2 to nu do su[nut]:=intmax; for k:=1 to nv do

begin break1:=true;

for nvt:=1 to nv do begin

i:=StrToInt(StringGrid1.Cells[1,nvt]);

j:=StrToInt(StringGrid1.Cells[2,nvt]); if su[i]<>intmax then

begin sunew:=su[i]+StrToInt(StringGrid1.Cells[3,nvt]); if sunew < su[j] then

begin

su[j]:= sunew; nuway[j]:=i; nvway[j]:=nvt; break1:=false;

end; end else

if su[j]<>intmax then begin

21

sunew:=su[j]+StrToInt(StringGrid1.Cells[3,nvt]); if sunew < su[i] then

begin

su[i]:= sunew; nuway[i]:=j; nvway[i]:=nvt; break1:=false; end;

end

end; {for nvt }

if break1 then break;

if k = nv then zeitnot:=true; end; {for k }

if su[nu]=intmax then

ShowMessage('Путь не существует или возможности программы '+ 'недостаточны для его отыскания.')

else

if zeitnot then

ShowMessage('Найденный путь возможно не оптимальный.'); k:=1; i:=nu; ushort[k]:=i;

repeat

i:=nuway[i]; inc(k); ushort[k]:=i; until i=1;

kushort:=k;

Label2.Caption:='Один из кратчайших путей проходит через узлы: '; for k:=kushort downto 1 do Label3.Caption:=Label3.Caption+Inttostr(ushort[k])+#32; Label5.Caption:=IntToStr(su[nu]);

end;

procedure TForm1.Edit1Change(Sender: TObject); begin

if Edit1.Text<>'' then StringGrid1.RowCount:=StrToInt(Edit1.Text)+1;

end;

procedure TForm1.Proverka(Sender: TObject); var k:integer;

begin

for k:=1 to nv do begin

if StrToInt(StringGrid1.Cells[1,k])=0

then ShowMessage('Проверьте содержимое ячейки');

if StrToInt(StringGrid1.Cells[2,k])=0

then ShowMessage(' Проверьте содержимое ячейки');

if ((StrToInt(StringGrid1.Cells[1,k]))>nu) then ShowMessage(' Проверьте содержимое ячейки');

if ((StrToInt(StringGrid1.Cells[2,k]))>nu) then ShowMessage(' Проверь содержимое ячейки'); end;

end;

procedure TForm1.FormCreate(Sender: TObject); begin

StringGrid1.Cells[0,0]:='№ ветви'; StringGrid1.Cells[1,0]:='Узел 1'; StringGrid1.Cells[2,0]:='Узел 2'; StringGrid1.Cells[3,0]:='Длина';

end;

end.

22

Работа 6. Поиск пути обхода конем всех полей шахматной доски

Задание. Составить приложение в системе Delphi 7 для решения задачи методом направленного перебора вершин дерева решений с возвратом из тупиков.

Описание алгоритма. Конь, стоящий в центре доски, имеет возможность переместиться в одну из восьми возможных клеток, которым присвоены порядковые номера от 1 до 8 (рис. 1).

3 2

41

K

58

6 7

Рис. 1. Возможные ходы шахматного коня

Путь коня в процессе обхода всех полей кодируется последовательностью чисел из указанного множества, которые записываются в вспомогательный массив {P} длиной 63 элемента, образуя код пути (рис. 2). Каждый проверочный ход осуществляется в свободную клетку с минимальным номером, и перемещение по вершинам дерева решений в процессе поиска происходит в сторону увеличения кода пути. При выборе очередного хода действуют следующие ограничения. Во-первых, конь не может выйти за пределы доски, во-вторых, он не может оказаться дважды на каком-либо поле. Если для очередного хода свободных клеток нет и решение еще не найдено, то для выхода из тупика осуществляется возврат в предыдущую клетку.

Разработка приложения

Рис. 2. Результаты решения задачи

23

Указания по выбору и размещению компонентов на форме

Компоненты Label1, Label2, Label3, Label4 служат для вывода символьной информации, компоненты Button1, Button2 служат для запуска соответствующих программ-обработчиков событий.

Компонент StringGrid1 “Таблица строк” предназначен для отображения результатов решения задачи в виде таблицы 8х8. С помощью настроечной панели Object Inspector этому компоненту заданы следующие значения свойств:

ColCount = 8, RowCount = 8, FixedCols = 0, FixedRows = 0, DefaultColWidth = 48, DefaultRowHeight = 48, Left = 280, Top = 42, Width = 390, Height = 390, ScrollBars = ssNone.

Компонент ProgressBar1 “Индикатор” предназначен для информирования пользователя о динамике вычислительного процесса в виде диаграммы-строки, поскольку для решения данной задачи на современном компьютере требуется около 10 секунд. Этому компоненту с помощью Object Inspector заданы следующие значения свойств: Left = 280, Top = 460, Width = 390, Height = 25, Min = 0, Max = 55.

В программе для индикации используется свойство ProgressBar1.Position, которому присваиваются целочисленные значения. После решения задачи и вывода результатов этот компонент при помощи метода ProgressBar1.Hide можно сделать невидимым.

Исходный модуль (жирным шрифтом выделен текст, формируемый системой

unit Chess_knight; interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, Grids, StdCtrls, ExtCtrls, ComCtrls; type

TForm1 = class(TForm)

Button1: TButton; Button2: TButton;

Label1: TLabel; Label2: TLabel; Label3: TLabel; Label4: TLabel; StringGrid1: TStringGrid; ProgressBar1: TProgressBar; procedure FormCreate(Sender: TObject);

procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject);

private

{Private declarations } public

{Public declarations }

end;

Form1: TForm1; a:ta; p:tp;

implementation

{$R *.dfm}

// - - - - - - - - - - - - - -

24

procedure TForm1.FormCreate(Sender: TObject); begin

WindowState:=WsMaximized;

end;

procedure TForm1.Button1Click(Sender: TObject); var

meg,chod,count_tupic:longint; i,j,k,kbeg,i1,j1,it,jt,count,step:integer; tupik:boolean; ss:string;

begin

for i:=1 to 8 do

for j:=1 to 8 do a[i,j]:=0; it:=1; jt:=1; a[it,jt]:=1; count:=0; meg:=0; step:=0; kbeg:=1;

count_tupic:=0; tupik:=false; ss:=''; repeat

for k:=kbeg to 9 do begin

if k = 9 then

begin tupik:=true; inc(count_tupic); break end; i1:=it+di[k];

if (i1 > 8) or (i1 < 1) then continue; j1:=jt+dj[k];

if (j1 > 8) or (j1 < 1) then continue; if a[i1,j1] > 0 then continue; inc(count); p[count]:=k; a[i1,j1]:=count+1; it:=i1; jt:=j1; kbeg:=1;

break;

end;

if tupik then begin

k:=p[count]; p[count]:=0; dec(count); a[it,jt]:=0; it:=it-di[k]; jt:=jt-dj[k]; kbeg:=k+1; tupik:=false;

end;

inc(step);

if step=1000000 then

begin inc(meg); step:=0; Progressbar1.Position:=meg end; until count = 63;

for i:=1 to 8 do for j:=1 to 8 do

StringGrid1.Cells[j-1,i-1]:=inttostr(a[i,j]); for i:=1 to 63 do ss:=ss+inttostr(p[i]); Label2.Caption:= Label2.Caption+ss; chod:=1000000*meg+step;

Label1.Caption:= Label1.Caption+inttostr(chod); Label4.Caption:= Label4.Caption+inttostr(count_tupic); Progressbar1.Hide;

end;

procedure TForm1.Button2Click(Sender: TObject); begin close end;

end.

Выводы. Разработанная программа успешно решила поставленную задачу. В процессе поиска решения был сделан 54482161 ход.

25

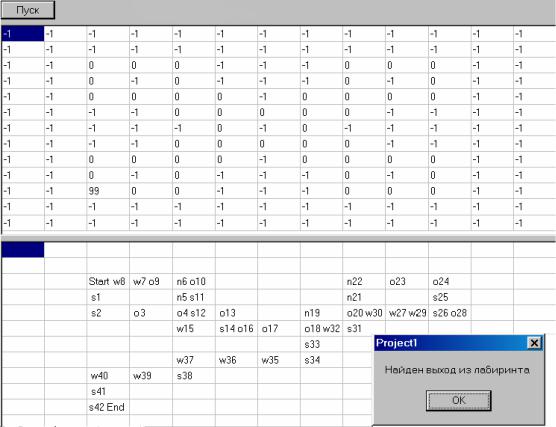
Работа 7. Лабиринтная задача

Задание. Разработать приложение средствами инструментальной системы Delphi для нахождения пути из начальной клетки к выходу из лабиринта. Результатом работы программы является таблица, которая фиксирует все перемещения агента в процессе поиска заданной клетки, соответствующей выходу из лабиринта.

Постановка задачи. Схема лабиринта задана в виде таблицы размером 13×13. В ней символами «-1» обозначены непроходимые клетки, а символом «0» – свободные клетки, через которые агент может перемещаться без ограничения на количество проходов. Движение агента может осуществляться по свободным клеткам в горизонтальном и вертикальном направлениях. Путь агента начинается в одной из свободных клеток. В данном примере ее координаты 2,2 (нумерация с нуля), выходом из лабиринта считается клетка, в которой записано число 99.

Рис. 1. Схема лабиринта и результаты работы программы

Описание алгоритма. Используем алгоритм с предпочтением наименее исследованных направлений. Введем вспомогательную целочисленную матрицу В размерности 13×13. Непроходимым клеткам лабиринта в этом массиве поставим в соответствие предельно большие числа, для каждой проходимой клетки значения элементов учитывают количество уже состоявшихся посещений. Предпочтительным считается то направление, которому соответствует минимальное значение среди значений элементов матрицы В, примыкающих к текущей клетке. Направление движения агента кодируется символами: n – вверх, s – вниз, w – влево, o – вправо.

Для представления исходных данных и результатов используются компоненты TStringGrid. Для ускорения отладки формирование структуры лабиринта осуществляется программным способом с помощью процедур track_cod и free_way.

В программном модуле жирным шрифтом выделены фрагменты, генерируемые системой.

26

Текст программного модуля

unit U021208; interface

uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Grids; type

TForm1 = class(TForm) Button1: TButton;

StringGrid1: TStringGrid; StringGrid2: TStringGrid; procedure Button1Click(Sender: TObject);

private { Private declarations } public { Public declarations } end;

const n=12;

dii:array[1..4] of integer=(1,0,-1,0); djj:array[1..4] of integer=(0,1,0,-1); archar:array[1..4] of char=('s','o','n','w');

var

Form1: TForm1; a,b:array[0..n+1,0..n+1] of integer; p:array[0..n*n] of integer;

i,di,j,dj,i1,j1,k,dk,ksave,n3,len:integer; implementation

{$R *.dfm}

{Задание последовательности поворотов для прокладки проходов} procedure track_cod;

var l,l1:integer; begin

n3:=n div 3;

for l1:=1 to n3 do begin

l:=(l1-1)*6+1;

p[l]:=1; p[l+1]:=1; p[l+2]:=0; p[l+3]:=1; p[l+4]:=1; p[l+5]:=2;

end;

end;

{Процедура прокладки проходов} procedure free_way(i,j,k:integer);

di:=dii[k]; dj:=djj[k]; i:=i+di; j:=j+dj;

end;

i1:=i; j1:=j; end;

procedure wrt_mat(StringGrid1:TstringGrid);{Вывод схемы лабиринта} var i,j:integer;

begin

for i:=0 to n+1 do for j:=0 to n+1 do

StringGrid1.Cells[j,i]:=inttostr(a[i,j])

end;

27

procedure TForm1.Button1Click(Sender: TObject); const intmax=255*256;

var kt,bmin:integer; begin

for i:=0 to n+1 do for j:=0 to n+1 do

a[i,j]:= -1; track_cod; free_way(2,2,2); free_way(n-2,2,3); free_way(2,n-2,1); a[i1,j1]:=99; free_way(n-2,n-2,4); wrt_mat(StringGrid1); for i:=0 to n+1 do

for j:=0 to n+1 do

if a[i,j] = 0 then b[i,j]:=0 else b[i,j]:= intmax; i:=2; j:=2; StringGrid2.Cells[j,i]:='Start '; len:=1;

dk:=1; bmin:=intmax+1; for kt:=1 to 4 do

begin

k:=k+dk; dk:=-1;

if k<=0 then k:=k+4; if k>=5 then k:=k-4;

begin StringGrid2.Cells[j,i]:=archar[k]+inttostr(len)+' End'; showmessage(' Найден выход из лабиринта.'); close end;

if b[i,j] < bmin then begin bmin:=b[i,j]; ksave:=k end; i:=i-di; j:=j-dj;

end; {for kt}

di:=dii[ksave]; dj:=djj[ksave]; i:=i+di; j:=j+dj; StringGrid2.Cells[j,i]:=StringGrid2.Cells[j,i]+

' '+archar[ksave]+inttostr(len); inc(b[i,j]); inc(len);

until len > n*n;

showmessage(' Выход из лабиринта не может быть найден.'); halt end;

end.

Выводы. Разработанная программа успешно решила поставленную задачу. Выход из данного лабиринта найден за 42 хода.

28

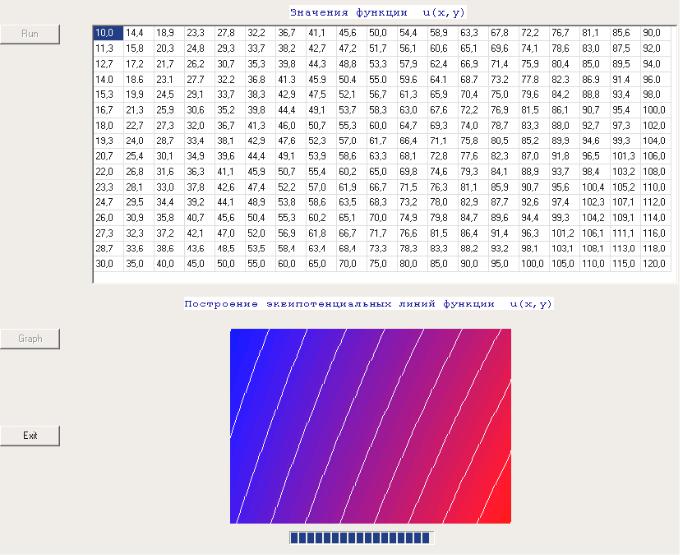
Работа 8. Построение картины стационарного плоского поля в прямоугольной области

Задание. Решить численным методом краевую задачу Дирихле для уравнения Лапласа:

.

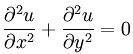Исходными данными являются значения функции в вершинах прямоугольной области, значения в остальных точках на границе области (т.е. по периметру прямоугольника) находятся путем линейной интерполяции. Результатом решения задачи является нахождение значений функции на множестве внутренних узлов указанной области.

Математической моделью данной задачи является система линейных алгебраических уравнений (СЛАУ), порядок которой определяется числом внутренним узлов. Программа должна обеспечивать автоматическое формирование коэффициентов и решение СЛАУ, например, методом Гаусса. Решение для большей наглядности следует представить в графической форме, при этом значения функции отображаются цветом точек прямоугольной области (синий цвет используется для наименьших значений функции, красный – для наибольших).

Рис. 1. Вид экранной формы приложения с результатами решения

29

Указание. Для представления решения в графической форме необходимо получить массив чисел с достаточно большой размерностью (примерно 240 на 340 точек). Для этого используется алгоритм двойной двумерной интерполяции. На первом этапе решение находится для сетки 15×18, а затем каждый элементарный прямоугольник покрывается сеткой такой же размерности, причем для расчета значений функции на обоих этапах используется одна и та же процедура.

unit U111108; // Задача Дирихле для уравнения Лапласа в прямоугольной interface // области с выводом решения в графической форме

uses // на базе алгоритма двойной двумерной интерполяции

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,

Forms, Dialogs, Grids, StdCtrls, ExtCtrls, ComCtrls;

Type // Жирным шрифтом выделены фрагменты, генерируемые системой

TForm1 = class(TForm)

Button1: TButton; Button2: TButton; Button3: TButton; Label1: TLabel; Label2: TLabel;

StringGrid1: TStringGrid; Image1: TImage; ProgressBar1: TProgressBar;

procedure FormCreate(Sender: TObject); procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject);

private

{Private declarations } public

{Public declarations }

end;

const i5=15; j6=18; n=(i5-1)*(j6-1); eps=1.0e-06; u00=10; u50=30; u06=90; u56=120;

type tu=array [0..i5,0..j6] of real; var

Form1: TForm1; u,unew:tu; umin,scale:real;

implementation

{$R *.dfm}

//Процедура вывода двумерного массива procedure wrt_u;

var i,j:byte; begin

for i:=0 to i5 do for j:=0 to j6 do

Form1.StringGrid1.Cells[j,i]:=floattostrf(u[i,j],ffFixed,7,1);

end;

//Вычисление коэффициентов СЛАУ и ее решение методом Гаусса procedure Lap(u1,u2,u3,u4:real; var u:tu);

var a:array [1..n,1..n] of real; b,x:array [1..n] of real; i,j,i1,j1,k,m:integer; du,h,s:real;

begin

u[0,0]:=u1; u[i5,0]:=u2; u[0,j6]:=u3; u[i5,j6]:=u4; du:=(u[0,j6]-u[0,0])/j6;

for j:=1 to j6-1 do u[0,j]:=u[0,0]+du*j;

du:=(u[i5,0]-u[0,0])/i5; for i:=1 to i5-1 do

30