
3136
.pdf3136 |
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ |
|
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА |
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САМАРСКИЙ ГОУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра муниципального пассажирского транспорта
АВТОМАТИЧЕСКИЕ КОМПЛЕКСЫ СИСТЕМ УПРАВЛЕНИЯ ГОРОДСКОГО ЭЛЕКТРИЧЕСКОГО ТРАНСПОРТА
Методические указания к выполнению контрольной работы для студентов специальности 140606 «Электрический транспорт» заочной формы обучения
Составитель: Е.В. Шищенко
Самара
2012
1
УДК 681.5: 658.284
Автоматические комплексы систем управления городского электрического транспорта : методические указания к выполнению контрольной работы для студентов специальности 140606 «Электрический транспорт» заочной формы обучения / составитель Е.В. Шищенко. – Самара : СамГУПС, 2012. – 11 с.
Приведены методические указания по выполнению контрольной работы для студентов-заочников по рассматриваемой дисциплине.
В методических указаниях содержатся основные сведения об определении передаточных функций автоматических систем управления. Рассмотрены критерии определения устойчивости автоматических систем управления. Представлены исходные данные для выполнения контрольного задания, состоящего из трех задач.
Утверждены на заседании кафедры «Муниципальный пассажирский транспорт»
19.12.2012 г., протокол № 4.
Печатаются по решению редакционно-издательского совета университета.
Составитель: Шищенко Елена Вячеславовна
Рецензенты: к.т.н., профессор, заведующий кафедрой «Муниципальный пассажирский транспорт» СамГУПС С.А. Привалов; к.п.н., доцент кафедры «Автомобили и станочные комплексы» СамГТУ Л.Б. Гаспарова
Подписано в печать 27.12.2012. Формат 60×90 1/16. Усл. печ. л. 0,7. Тираж 50 экз. Заказ 308.
© Самарский государственный университет путей сообщения, 2012
2
КОНТРОЛЬНОЕ ЗАДАНИЕ
Каждый студент выполняет свое задание, состоящее из двух задач по своему варианту, согласно табл. 1, табл. 2.
Таблица 1
Исходные данные для выполнения задачи № 1 контрольного задания
Вари- |
|
Схема 1 |
|
|
|
Схема 2 |
|
|
|
|
Схема 3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ант |
W1(p) |
|
W2(p) |
|
Wос(p) |
W1(p) |
W2(p) |
|
W3(p) |
W4(p) |
Wос(p) |
W1(p) |
W2(p) |
W2(p) |
Wосдоп(p) |
Wос(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
2 |
|
+1 |
3 |
4 |
|
5 |
6 |
–1 |
6 |
8 |
9 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
3 |
|
–1 |
4 |
5 |
|
6 |
7 |
+1 |
8 |
9 |
10 |
–1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
4 |
|
+1 |
5 |
6 |
|
7 |
8 |
–1 |
9 |
10 |
11 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
5 |
|
–1 |
6 |
7 |
|
8 |
9 |
+1 |
10 |
11 |
12 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
6 |
|
+1 |
7 |
8 |
|
9 |
10 |
–1 |
11 |
12 |
13 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
|
7 |
|
–1 |
8 |
9 |
|
10 |
11 |
+1 |
12 |
13 |
14 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
7 |
|
8 |
|
+1 |
9 |
10 |
|
11 |
12 |
–1 |
13 |
14 |
15 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
8 |
|
9 |
|
–1 |
10 |
11 |
|
12 |
13 |
+1 |
14 |
15 |
16 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
9 |
|
10 |
|
+1 |
11 |
12 |
|
13 |
14 |
–1 |
15 |
16 |
17 |
–1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
10 |
|
11 |
|
–1 |
12 |
13 |
|
14 |
15 |
+1 |
16 |
17 |
18 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
11 |
|
12 |
|
+1 |
13 |
14 |
|
15 |
16 |
–1 |
17 |
18 |
19 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
12 |
|
13 |
|
–1 |
14 |
15 |
|
16 |
17 |
+1 |
18 |
19 |
20 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
13 |
|
14 |
|
+1 |
15 |
16 |
|
17 |
18 |
–1 |
19 |
20 |
21 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
14 |
|
15 |
|
–1 |
16 |
17 |
|
18 |
19 |
+1 |
20 |
21 |
22 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
15 |
|
16 |
|
+1 |
17 |
18 |
|
19 |
20 |
–1 |
21 |
22 |
23 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
16 |
|
17 |
|
–1 |
18 |
19 |
|
20 |
21 |
+1 |
22 |
23 |
24 |
+1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
17 |
|
18 |
|
+1 |
19 |
20 |
|
21 |
22 |
–1 |
23 |
24 |
25 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
18 |
|
19 |
|
–1 |
20 |
21 |
|
22 |
23 |
+1 |
24 |
25 |
26 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
19 |
|
20 |
|
–1 |
21 |
22 |
|
23 |
24 |
+1 |
25 |
26 |
27 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
20 |
|
21 |
|
+1 |
22 |
23 |
|
24 |
25 |
–1 |
26 |
27 |
2 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
21 |
|
22 |
|
+1 |
23 |
24 |
|
25 |
26 |
–1 |
27 |
2 |
3 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
22 |
|
23 |
|
–1 |
24 |
25 |
|
26 |
27 |
–1 |
2 |
3 |
4 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
23 |
|
24 |
|
–1 |
25 |
26 |
|
27 |
2 |
–1 |
3 |
4 |
5 |
+1 |
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
24 |
|
25 |
|
–1 |
26 |
27 |
|
2 |
3 |
–1 |
4 |
5 |
6 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
25 |
|
26 |
|
–1 |
27 |
2 |
|
3 |
4 |
+1 |
5 |
6 |
7 |
–1 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
Таблица 2 |
|
|
Исходные данные для выполнения задачи № 2 контрольного задания |
|
|||||
|
|
|
|
|
|
|
|
Вариант |
|
Коэффициенты характеристического уравнения |
|
||||
|
|
|
|
|
|
||
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
||
|
|||||||
|
|
|
|
|
|
|
|
1 |
0 |
–3 |
4 |
1 |
–3 |
2 |
|
|
|
|
|
|
|
|
|
2 |
1 |
–4 |
0 |
8 |
3 |
2 |
|
|
|
|
|
|
|
|
|
3 |
2 |
–4 |
3 |
8 |
0 |
1 |
|
|
|
|
|
|
|
|
|
4 |
3 |
0 |
–3 |
8 |
2 |
1 |
|
|
|
|
|
|
|
|
|
5 |
4 |
2 |
3 |
–4 |
–2 |
7 |
|
|
|
|
|
|
|
|
|
6 |
0 |
2 |
–4 |
4 |
1 |
3 |
|
|
|
|
|
|
|
|
|
7 |
–8 |
5 |
4 |
–4 |
1 |
3 |
|
|
|
|
|
|
|
|
|
8 |
–6 |
–3 |
0 |
4 |
2 |
5 |
|
|
|
|
|
|
|
|
|
9 |
–7 |
–3 |
4 |
4 |
2 |
5 |
|
|
|
|
|
|
|
|
|
10 |
–1 |
0 |
4 |
7 |
2 |
5 |
|
|
|
|
|
|
|
|
|
11 |
–1 |
3 |
4 |
7 |
–2 |
5 |
|
|
|
|
|
|
|
|
|
12 |
2 |
6 |
–4 |
0 |
3 |
–1 |
|
|
|
|
|
|
|
|
|
13 |
0 |
6 |
–5 |
1 |
3 |
–4 |
|
|
|
|
|
|
|
|
|
14 |
3 |
–5 |
5 |
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
15 |
–5 |
3 |
5 |
2 |
1 |
4 |
|
|
|
|
|
|
|
|
|
16 |
–5 |
0 |
7 |
2 |
3 |
1 |
|
|
|
|
|
|
|
|
|
17 |
–5 |
5 |
8 |
0 |
–3 |
2 |
|
|
|
|
|
|
|
|
|
18 |
0 |
3 |
–8 |
2 |
4 |
–3 |
|
|
|
|
|
|
|
|
|
19 |
1 |
–3 |
0 |
2 |
4 |
8 |
|
|
|
|
|
|
|
|
|
20 |
1 |
–3 |
5 |
–2 |
4 |
0 |
|
|
|
|
|
|
|
|
|
21 |
0 |
3 |
5 |
2 |
7 |
4 |
|
|
|
|
|
|
|
|
|
22 |
–2 |
2 |
5 |
1 |
7 |
3 |
|
|
|
|
|
|
|
|
|
23 |
–2 |
0 |
–5 |
1 |
7 |
4 |
|
|
|
|
|
|
|
|
|
24 |
2 |
1 |
8 |
3 |
0 |
4 |
|
|
|
|
|
|
|
|
|
25 |
2 |
1 |
0 |
7 |
–4 |
8 |
|
|
|
|
|
|
|
|
|
4
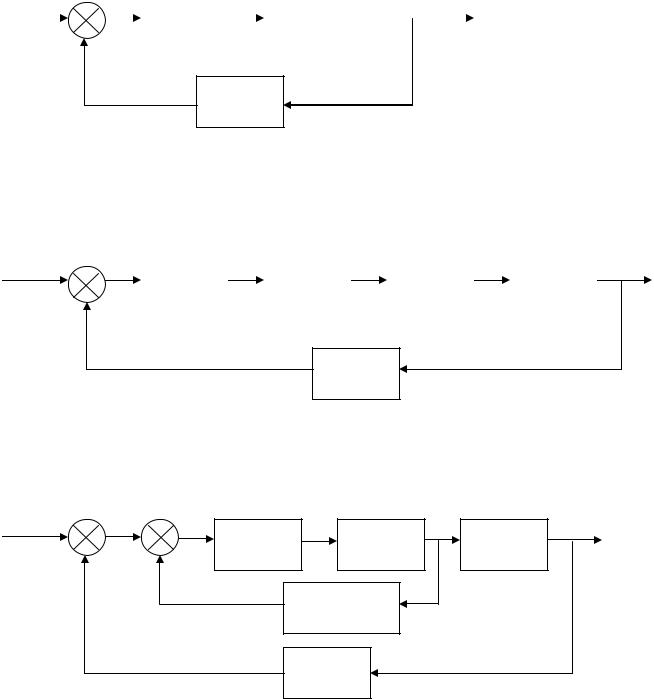
ЗАДАЧА № 1. Определить передаточную функцию АСУ, имеющую соответствующую структурную схему, показанную на рис. 1, 2, 3, согласно заданию.
х |
|
|
|
y |
W1(p) |
|
W2(p) |
||
|
|
|
||
|
|
|
|
|
WОС(p)
Рис. 1. Структурная схема 1
х |
|
|
|
|
|
|
|
у |
W1(p) |
|
W2(p) |
|
W3(p) |
|
W4(p) |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
WОС(p)
Рис. 2. Структурная схема 2
х |
W1(p) |
W2(p) |
W3(p) |
у |
|
|
WОСДОП(p)
WОС(p)
Рис. 3. Структурная схема 3
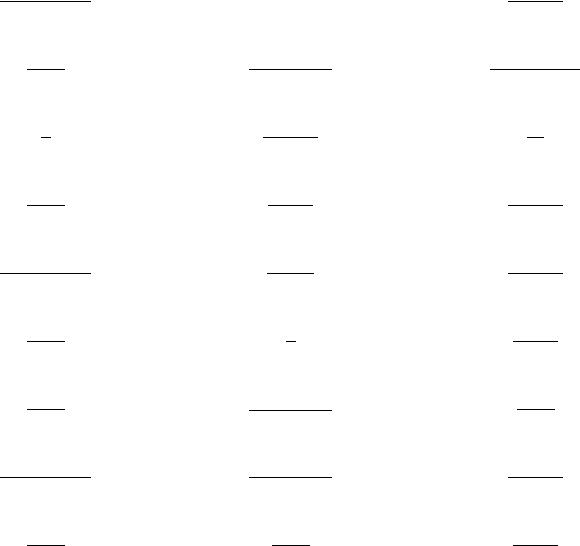
Передаточная функция каждого звена выбирается по варианту индивидуального задания табл. 1. Звенья АСУ представлены в табл. 3.
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
||||
|
|
|
|
|
|
|
|
Звенья АСУ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
№ |
Передаточная |
№ |
Передаточная |
№ |
Передаточная |
|||||||||||||||||
п/п |
|
функция |
|
|
п/п |
функция |
п/п |
функция |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
3 |
|
|
1 |
|
10 |
|
|
|
|
|
|
|
19 |
2 |
2 |
1 |
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
2 |
1 |
|
|
|
11 |
5 |
1 |
20 |
3 |
|
3 |
1 |
|
|||||||
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|||||||||||
3 |
|
3 |
|
|
|
|
12 |
|
3 |
1 |
|
21 |
|
|
4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
4 |
1 |
|
|
|
13 |
|
3 |
2 |
|
|
22 |
4 |
3 |
|
|
|
|
|||
5 |
2 |
4 |
|
|
1 |
|
14 |
|
4 |
1 |
|
|
23 |
|
|
2 |
3 |
|
|
|
||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
6 |
|
3 |
1 |
|
|
|
15 |
|
|
4 |
|
|
|
|
24 |
|
|
3 |
3 |
|
|
|
7 |
|
4 |
1 |
|
|
|
16 |
5 |
1 |
25 |
|
|
2 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
8 |
3 |
4 |
|
|
1 |
|
17 |
2 |
1 |
26 |
2 |
3 |
1 |
|
|
|||||||
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
9 |
|
3 |
1 |
|
|
|
18 |
|
1 |
1 |
|
|
|
27 |
|
|
4 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ЗАДАЧА № 2. Определить по критериям Рауса, Гурвица и Михайлова устойчивость АСУ, имеющего следующее характеристическое уравнение:
0.
Значения коэффициентов уравнения выбираются согласно заданию по табл. 2.
6
МЕТОДИКА ОПРЕДЕЛЕНИЯ УСТОЙЧИВОСТИ АСУ
Критерий Рауса. Методика определения устойчивости АСУ по критерию Рауса представляет собой последовательность математических операций, осуществляемых при решении задачи и является довольно простым методом анализа характеристического уравнения системы:
0. (1)
Уравнение записывают так, что значение а0 > 0. Затем составляют матрицу из коэффициентов исходного характеристического уравнения. Для этого выписывают строку с четными, затем, под ней – строку с нечетными коэффициентами характеристического уравнения. Остальные коэффициенты в нижестоящих строках выражают через коэффициенты вышестоящих строк. Всего в таблице будет n+1 строк.
Таким образом, матрица, составленная из коэффициентов характеристического уравнения будет иметь вид:
|
|
|
|
|
|
а0 а2 а4 … |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
а1 а3 |
а5 |
… |
|
|
|
||
|
|
|
|
|
|
b0 b2 b4 |
… |
|
, |
(2) |
|||
|
|
|
|
|
|
b1 b3 b5 … |
|
|
|
||||
|
|
|
|
|
|
c0 c0 |
c0 … |
|
|
|
|||
|
|
|
|
. |
. |
. … |
|
|
|
||||
|
|
|
|
. |
. |
. … |
|
|
|
||||
где |
|
; |
|
; |
|
|
|
|
|
ит.д. |
(3) |
||
|
|
|
|
|
|
|
|||||||
Чаще всего эти коэффициенты записывают следующим образом:
; |
; |
|
|
; |
(4) |
||
; |
|||
и т. д. |
|
||
; |
ит.д. |
|
7

Условие устойчивости: система устойчива, если все элементы первого столбца таблицы Рауса имеют одинаковые знаки, совпадающие со знаком коэффициента а0, т. е. а0 > 0, а1 > 0, b0 > 0, b1 > 0 и т. д. Если какой-то один из членов первого столбца равен нулю, то система находится на границе устойчивости.
Критерий Гурвица. Методика определения устойчивости АСУ по критерию Гурвица, подобно определению по критерию Рауса, основан на определенной табличной записи коэффициентов характеристического уравнения и формулирует условие устойчивости в зависимости от знаков некоторых определителей.
Определитель Гурвица записывают следующим образом. Все коэффициенты от а0 до аn располагают по главной диагонали в порядке возрастания индексов. Вверх от главной диагонали, в столбцах записывают коэффициенты характеристического уравнения с последовательно возрастающими, а вниз – с убывающими индексами. На месте коэффициентов, индексы которых больше чем n и меньше чем 0 проставляют нули, например:
|
a1 |
a3 |
a5 |
… 0 |
|
|
|
|
a0 |
a2 |
a4 |
… 0 |
|
|
|
∆n = |
0 a1 a3 … 0 |
|
. |
(5) |
|||
|
… … … … 0 |
|
|
|
|||
|
0 … … … an |
|
|
|
|||
|
|
|
|||||
Условие устойчивости: система устойчива тогда и только тогда, когда все диагональные миноры определителя больше нуля, т. е. совпадают со знаком первого коэффициента а0:
∆0;
∆0;
∆2 = |
|
а1 |
а3 |
|
> 0; |
|
|
||||
|
|||||
|
|
а0 |
а2 |
|
|
|
|
|
|
а1 а3 а5
∆3 = а0 а2 а4 > 0.
0 а1 а3
В практических расчетах устойчивость системы определяют по критерию устойчивости Гурвица следующим образом.
Для устойчивых систем характеристические уравнения первого и второго порядка должны иметь положительные коэффициенты: а0 > 0; а1 > 0.
Применительно к уравнениям более высоких порядков, кроме положительных значений коэффициентов а0 > 0; а1 > 0… аn-1 > 0; аn > 0, необходимо соблюдение следующих соотношений.
8

Для уравнения |
|
0, |
|
(6) |
|
|
|
||
условие устойчивости |
∆2 = а1а2 – а0а3 > 0. |
0, |
|
(7) |
Для уравнения |
|
|
(8) |
|
условие устойчивости |
∆3 = а3 (а1а2 – а0 а3) – а4а12 > 0. |
|
(9) |
|
Для уравнения |
|
0, |
|
(10) |
условия устойчивости |
∆2 = а1а2 – а0а3 > 0; |
|
(11) |
|
|
|
|||
|
∆4 = (а1а2 – а0 а3)(а3а4 – а2а5)( а1а4 – а0а5)2 > 0. |
0, |
(12) |
|
Для уравнения |
|
|
(13) |
|
условия устойчивости |
∆3 = а3 (а1а2 – а0 а3) – а4а12 > 0; |
|
(14) |
|
|
∆5 = (а1а2 – а0 а3)[а5(а3а4 – а2а5)+ а6(2а1а5 – а32)]+ |
|
(15) |
|
|
+ (а1а4 – а0а5)[ а1а3а6 − а5(а1а4 – а0а5)] > 0. |
|
|
|
Критерий Михайлова. Критерий устойчивости Михайлова относится к частотным критериям. Преимуществами частотных критериев считают их наглядность и возможность экспериментального определения частотных характеристик отдельных звеньев системы, когда для них трудно составить дифференциальные уравнения. Согласно рассматриваемому критерию, характеристическое уравнение любой степени можно представить в виде комплексного полинома:
|
, |
(16) |
где |
– вектор, амплитуда и фаза которого являются функциями частоты . |
|
Условие устойчивости: для устойчивости системы необходимо и достаточно, чтобы при изменении угловой частоты от 0 до ∞, годограф, описываемый концом вектора на плоскости комплексного переменного, начинался на вещественной положительной полуоси и, вращаясь против часовой стрелки, нигде не обращался в нуль, проходил последовательно число квадрантов, которое равно степени п характеристического уравнения, повернувшись на угол .
9
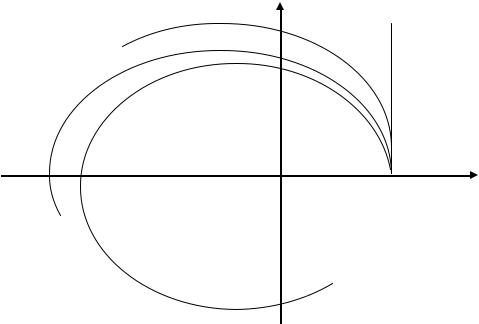
Пример годографа, описываемого вектором на |
на плоскости комплексного |
переменного устойчивой системы показан на рисунке. |
|
п = 2 |
п = 1 |
п = 3
п = 4
10
