Задания

Задание 2.1. Найти ранг матрицы

1. Методом единиц и нулей;

2. Методом окаймляющих миноров.

1. ;	2. ;
3. ;	4. ;
5. ;	6. ;
7. ;	8.;
9. ;	10. ;
11. ;	12. ;
13. ;	14. ;
15. ;	16. ;
17. ;	18. ;
19. ;	20. ;
21.;	22. ;
23. ;	24. ;
25. ;	26. ;
27. ;	28. ;
29. ;	30. .

0. Обратная матрица

Квадратная матрица порядка называетсяневырожденной, если её определитель (детерминант).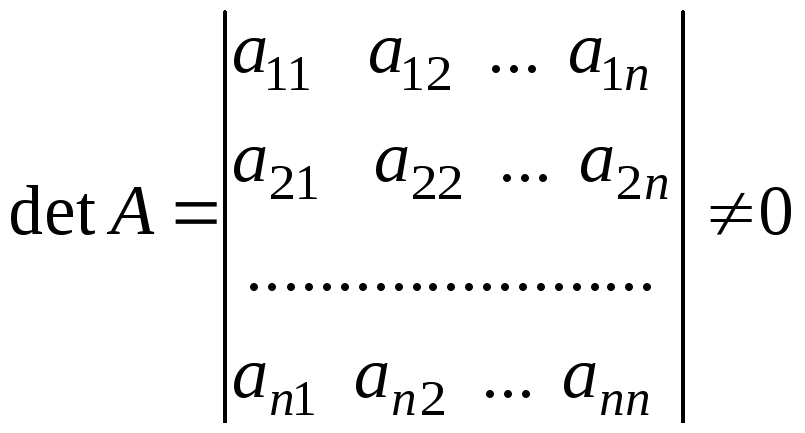

В случае, когда , матрицаназываетсявырожденной.

Только для квадратной невырожденной матрицывводится понятие обратной матрицы.

Матрица называетсяобратнойдля квадратной невырожденной матрицы, если, где- единичная матрица порядка.

Для матрицы существует единственная обратная матрица, которая определяется по формуле:

или,

где или-союзнаяилиприсоединённаяматрица, её элементами являются алгебраические дополнениятранспонированнойматрицы, т.е. матрицы, полученной из данной матрицызаменой её строк столбцами с теми же номерами.

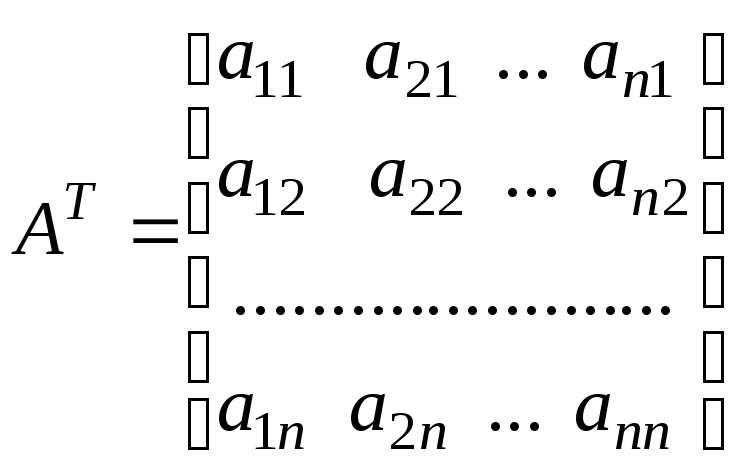, т.е.

Пример 2.2.Найти обратную матрицу двумя способами: с помощью алгебраических дополнений и путем элементарных преобразований. Сделать проверку.

Дана матрица .

Найти: .

Решение:

1 способ. С помощью алгебраических дополнений.

Найдем обратную матрицу по формуле ,

где - определитель матрицы;

- союзная или присоединённая матрица, состоящая из алгебраических дополнений транспонированной матрицы.

Согласно формуле можно сказать, что если , то обратная матрица не существует.

Найдем:

,

значит обратная матрица существует.

Составим союзную матрицу, для этого найдем алгебраические дополнения по формуле

;	;	;
;	;	;
;	;	.

Отсюда:

.

2 способ. Основан на элементарных преобразованиях вспомогательной матрицы, которая получается путём приписывания к данной матрице единичной матрицы того же порядка. Схематически это выглядит так:

Итак, запишем матрицу:

~~

~~~

~~

~~

~

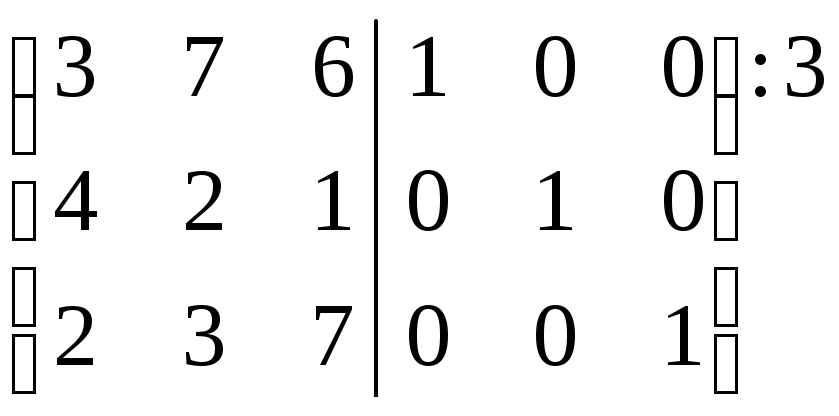
Итак:

Проверка. Сделаем проверку исходя из свойства. Остановимся на произведении. Для удобства умножения матрицзапишем в виде:

.

Тогда:

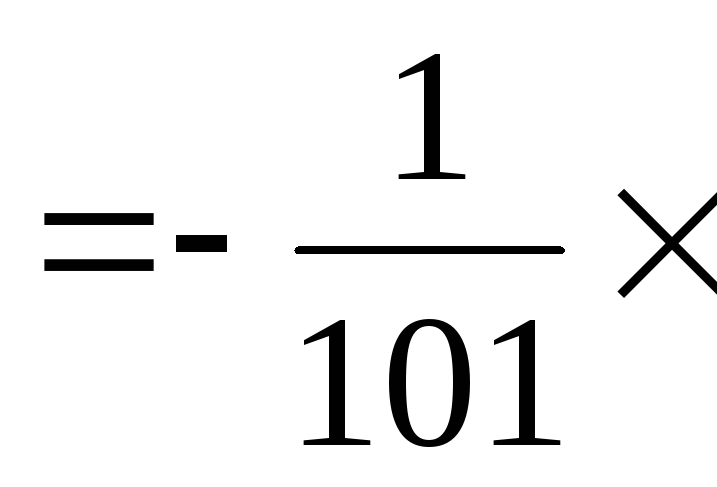
- верно (смотри определение)

Задание 2.2. Найти обратную матрицу двумя способами: с помощью алгебраических дополнений и путем элементарных преобразований. Сделать проверку.

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
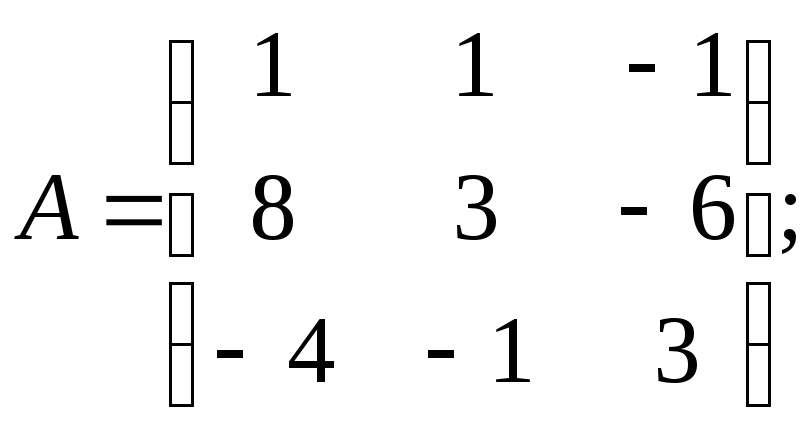
15.	16.
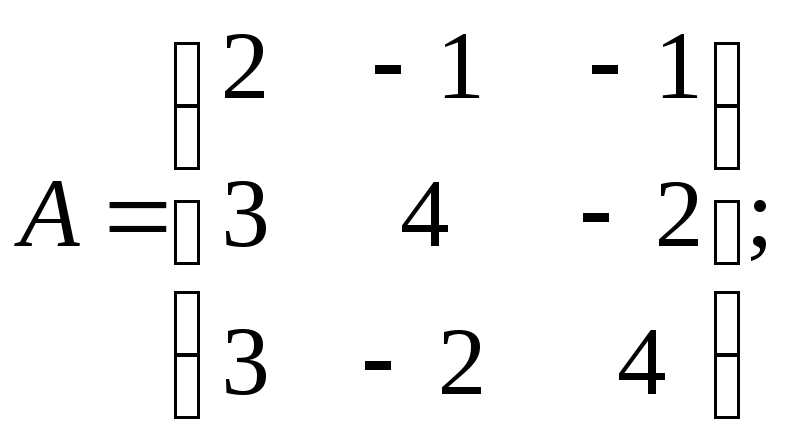
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

3. Системы линейных алгебраических уравнений