0. Элементарные преобразования матрицы. Ранг матрицы

Введем понятие ранга матрицы. Выделим в матрице -строк и -столбцов, где - число, меньшее или равное меньшему из чисели. Определитель порядка , составленный из элементов, стоящих из пересечения выделенных -строк и -столбцов, называетсяминоромилиопределителем, порожденным матрицей.

Рангом матрицы (обозначается) называется наибольший порядок порожденных ею определителей, отличных от нуля.

Ранг матрицы не изменится, если:

1. поменять местами любые два параллельных ряда;

2. умножить (разделить) каждый элемент ряда на один и тот же множитель (делитель) ;

3. прибавить к элементам ряда соответствующие элементы любого другого параллельного ряда, умноженные на один и тот же множитель;

4. Ряд, состоящий из нулей, отбрасывается.

Преобразования 1-4 называются элементарными. Две матрицы называютсяэквивалентными, если одна матрица получается из другой с помощью элементарных преобразований. Эквивалентность матрици обозначается ~.

Базисным минором матрицыназывается всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.

Рассмотрим основные методы нахождения ранга матрицы.

1. Метод единиц и нулей. С помощью элементарных преобразований можно любую матрицу привести к виду, когда каждый ее ряд будет состоять только из нулей, или нулей и одной единицы. Тогда число оставшихся единиц и определит ранг исходной матрицы, так как полученная матрица будет эквивалентна исходной.

Пример 2.1.Найти ранг матрицы методом единиц и нулей.

~

1 шаг.

Разделим элементы третьего столбца на 2, затем первую строку умножим на и сложим с четвертой строкой. Получим новую эквивалентную матрицу:

~~

2 шаг.

Теперь четвертую строчку складываем со второй и с третьей. Получим новую эквивалентную матрицу:

~~

+

++

3 шаг.

Умножим элементы второго столбца на и сложим с элементами четвертого столбца. Затем умножим элементы второго столбца наи сложим с соответствующими элементами первого столбца. И окончательно элементы второго столбца сложим с соответствующими элементами пятого столбца. Получим новую эквивалентную матрицу:

~~

4 шаг.

Умножим элементы третьей строки на и сложим с соответствующими элементами второй строки. Получим новую эквивалентную матрицу:

~~

+

5 шаг.

Сложим элементы пятого столбца с соответствующими элементами первого столбца. Получим новую эквивалентную матрицу:

~~

+

6 шаг.

Умножим элементы третьего столбца на 3 и сложим с соответствующими элементами первого столбца. Получим новую эквивалентную матрицу:

~~

++

7 шаг.

Умножим на элементы третьего столбца и сложим с соответствующими элементами второго и четвертого столбцов. Получим новую эквивалентную матрицу:

~~

+

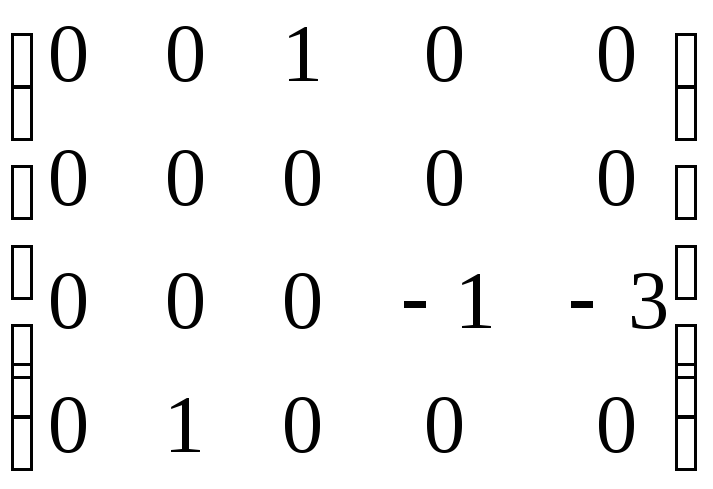8 шаг.

Умножим элементы четвертого столбца на и сложим с соответствующими элементами пятого столбца. Затем просто умножим элементы четвертого столбца на. Получим новую эквивалентную матрицу:

~- , так как осталось 3 единицы.

2. Метод окаймляющих миноров. Минорпорядка, содержащий в себе минорпорядка, называетсяокаймляющимминором. Если у матрицы существует минор, а все окаймляющие его миноры, то.

Найдем этим методом из предыдущего примера.

Начнем с левого верхнего угла:

;

;

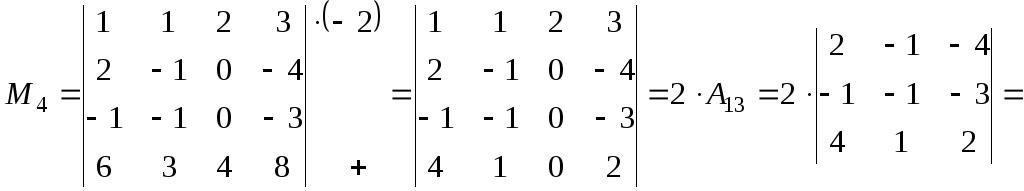
Как видно, что эта матрица содержит всего два минора 4-го порядка. Проверим второй:

То есть