§ 6 Интегрирования некоторых тригонометрических функций

а) Интегрирование вида где- рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки, в результате которой

_.

Пример. Найти интеграл

.

Решение. Применим универсальную тригонометрическую подстановку

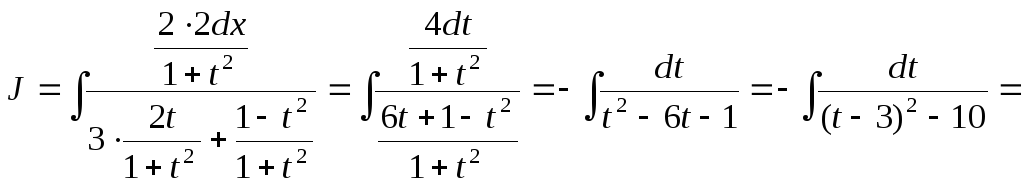
Вернемся к старой переменной

Универсальная подстановка во многих случаях приводит к сложным вычислениям. Если подынтегральная функция четная относительно синуса и косинуса, то удобнее применять упрощенную тригонометрическую подстановку

Пример.

Найти интеграл

Применим упрощенную тригонометрическую подстановку

Вернемся к старой переменной, получим

б) Интегралы вида

По крайней мере один из показателей или- нечетное положительное число. Если- нечетное положительное число, то применяется подстановка, если же-нечетное положительное число, то подстановка

Пример. Найти

Получим табличный интеграл

.

Вернемся к старой переменной

.

Случай 2. Оба показателя степени - четные положительные числа. Тогда подынтегральную функцию следует преобразовать с помощью тригонометрических функций

Пример. Найти интеграл

Решение: Преобразуем подынтегральное выражение

Получим

Случай 3

Для вычисления интегралов вида

где часто применяется метод интегрирования по частям. Он дает следующие формулы:

(применяется для ) (1)

(применяется для ) (2)

Эти формулы называются формулами понижения. Часто требуется неоднократное их применение.

Если, то используется одна из следующих формул, называемых формулами повышения.

(для ) (3)

(для ) (4)

Пример. Найти интеграл

Воспользуемся рекуррентной формулой (3)

Воспользуемся формулой (4) для нахождения интеграла

Воспользуемся формулой (3) для нахождения

Окончательно имеем:

Замечание! Применение формул 1-4 к интегралам вида не всегда является наиболее простым. Часто тригонометрические интегралы удобно брать с использованием тригонометрической единицы.

Пример. Найти интеграл

Решение.

в) Интегралы видаи, где- целое положительное число.

При нахождения таких интегралов применяются формулы

С помощью которых последовательно понижает степень тангенса или котангенса.

Пример. Найти интеграл

Интегралы вида

г), проще всего находится по рекуррентной формуле:

д) Интегралы вида

Берутся при преобразовании произведения в сумму с помощью следующих тригонометрических формул:

Например найти интеграл

Задание 6

Найти интегралы:

Вариант 1

1) a) б)

2) а)б)

3) а)б)в)

4) а)б)в)

5)

6) а)б)

7) а)б)в)

Вариант 2

1) а)б

2) а)б

3) а)бв)

4) а)б)в)

5)

6) а)б)

7) а)б)в)

Вариант 3

1) а)б)

2) а)б)

3) а)б)в)

4) а)б)в)

5)

6) а) б)

7) а) б)в)

Вариант 4

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 5

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 6

1) а) б)

2) а)б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 7

1) а)б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 8

1) а) б)

2) а) б)

3) а) б)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 9

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 10

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)

5)

6) а) б)

7) а) б)в)

Вариант 11

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 12

1) а) б)

2) а) б)

3) а) б)

4) а) б)в)

5)

6) а) б)

7) а)б)в)

Вариант 13

1) а) б)

2) а) б)

3) а) б)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 14

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 15

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 16

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 17

1) а) б)

2) а) б)

3) а) б)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 18

1) а)б)

2) а) б)

3) а) б)

4) а) б)в)

5)

6) а) б)

7) а) б) в)

Вариант 19

1) а) б)

2) а) б)

3) а) б)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 20

1) а) б)

2) а) б)

3) б)в)

4) а) б)в)

5)

6) а)б)

7) а) б)в)

Вариант 21

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 22

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 23

1) а) б)

2) а) б)

3) а) б)

4) аб)в)

5)

6) а) б)

7) а) б)в)

Вариант 24

1) а)б)

2) а) б)

3) а) б)в)

4) а) б)в)

5) а)

6) а) б)

6) а) б)в)

Вариант 25

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 26

1) а) б)

2) а) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 27

1) а) б)

2) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 28

1) а) б)

2) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 29

1) а) б)

2) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)

Вариант 30

1) а) б)

2) б)

3) а) б)в)

4) а) б)в)

5)

6) а) б)

7) а) б)в)