2. Основные методы интегрирования

Метод подстановки или замены переменной

Суть метода в том, что переменную интегрирования x заменяем на некоторое выражение, зависящее от новой переменной , где– непрерывная, вместе со своей производной, функция от аргументаt. Затем находим и переходим под интегралом к новой переменнойt. Вычислив этот интеграл, возвращаемся к исходной переменной x.

Соответствующая формула имеет вид

, (1)

В некоторых случаях, через новую переменную удобно заменить не x, а некоторое выражение, зависящее от x, т.е. сделать подстановку и, вычислив новый интеграл, вернуться к переменнойx:

. (2)

Пример 2. Вычислить интеграл .

Решение. Сделаем подстановку , тогдаи. Поэтому интеграл преобразуется к виду

.

Из подстановки найдеми. Тогда.

Таким образом, мы получили табличный интеграл

.

Пример 3. Вычислить интеграл .

Решение. Сделаем подстановку . Тогда. Переходя под интегралом к переменной, получим

.

Возвращаясь к переменной найдем окончательно.

Сделаем проверку , что совпадает с подынтегральным выражением.

Аналогичным образом вычислим еще несколько интегралов, не делая подробных объяснений.

Пример 4.

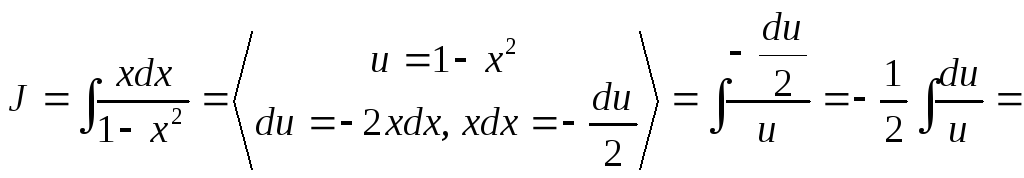
Пример 5. .

Пример 6. .

Пример 8.

Метод интегрирования по частям

Пусть даны две непрерывные в некоторой области функции и. Известно, что. Интегрируя левую и правую части этого равенства, получим

.

В левой части этого равенства находятся два симметричных по форме интеграла. Если один из них (например, второй) вычисляется просто, то другой (первый) можно вычислить по формуле

, (3)

которая и называется формулой интегрирования по частям.

Эта формула применяется для интегрирования достаточно широкого класса функций.

Пример 9. Вычислить интеграл .

Решение. Обозначим . Тогда, а(см. пример 7), по формуле (3) получим

Пример 10. Вычислить интеграл .

Решение.

(см. пример 4).

3. Интегрирование рациональных дробей

Рациональной дробью называется дробь вида , гдеи— многочлены степениисоответственно.

Если , то дробь называетсяправильной, если , то дробь называетсянеправильной. Неправильную рациональную дробь можно преобразовать, представив ее в виде суммы целой части и правильной рациональной дроби, например,

.

Разделим числитель на знаменатель «уголком»

Следовательно, .

Так как целая часть интегрируется легко, то задача сводится к интегрированию правильных рациональных дробей и решается в два этапа

1. Представление произвольной рациональной дроби в виде суммы простейших рациональных дробей.

2. Интегрирование простейших рациональных дробей.

К простейшим рациональным дробям относятся дроби вида

, где - натуральное число и дискриминант квадратного трехчленаменьше нуля,.

Вычислим интегралы от указанных дробей.

1. .

2.

.

3. .

Выделим в знаменателе полный квадрат

.

Обозначим

, тогда .

Таким образом,

.

Возвращаясь к исходной переменной, получим

,

где .

Рациональная дробь четвертого вида встречается достаточно редко, и ее интегрирование мы рассматривать не будем.

Схему разложения правильной рациональной дроби на простейшие покажем на примере.

Пусть знаменатель дроби уже представлен в виде произведения линейных и квадратных сомножителей (с отрицательным дискриминантом) различной кратности, например:

.

Тогда дробь можно представить в виде

(4)

Здесь каждому множителю знаменателя соответствует столько дробей, какова кратность этого множителя. Линейным множителям, в числителях, соответствуют постоянные числа, квадратным множителям – многочлены вида . Если множителей будет больше и их кратность выше, то правая часть соответствующим образом увеличивается. Для нахождения неизвестных коэффициентоввсе дроби в правой части приводятся к общему знаменателю (который будет равен знаменателю левой части) и приравниваются друг другу числители левой и правой части. Из этого сравнения получается система уравнений, из которой находятся все неизвестные коэффициенты.

Пример 11. Вычислить интеграл .

Решение. Представим подынтегральную дробь в виде суммы простейших дробей. Так как квадратный трехчлен имеет отрицательный дискриминант,, то

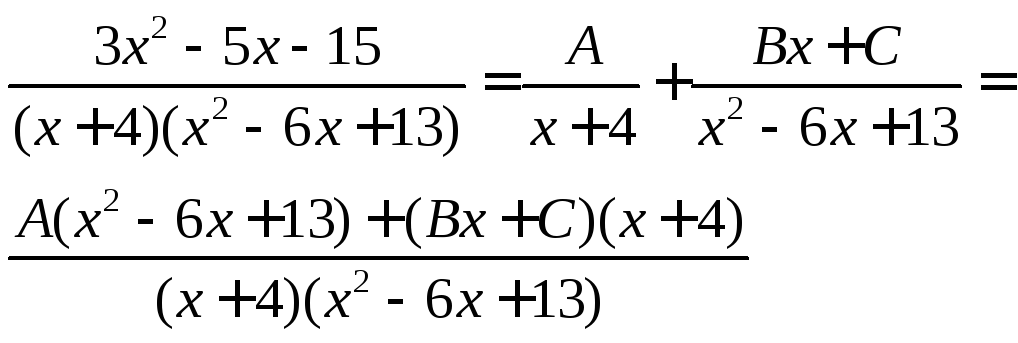
Отсюда получаем

или

или .

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях, получим:

Таким образом,

.