2. Вычисление двойных интегралов

Вычисление двойного интеграла сводится к двукратному применению формулы Ньютона-Лейбница (7). Пусть область D определена неравенствами , (рис.7).

рис. 7 рис. 8

Тогда формула для вычисления криволинейного интеграла имеет вид

, (11)

причем сначала вычисляется внутренний интеграл ,в котором переменная считается постоянной, а затем полученное выражение еще раз интегрируется по переменной x внешним интегрированием.

Если область D задана неравенствами (рис.8), то двойной интеграл вычисляется по формуле

. (12)

Здесь внутренний интеграл вычисляется по переменной x, при постоянном y, а внешний — по переменной y.

Интегрирование по произвольной области D сводится к применению формул (11) или (12).

Пример 1. Вычислить двойной интеграл двумя способами, изменяя порядок интегрирования: , гдеD — область, ограниченная линиями ,,.

Решение. Сделаем чертеж (рис.9)

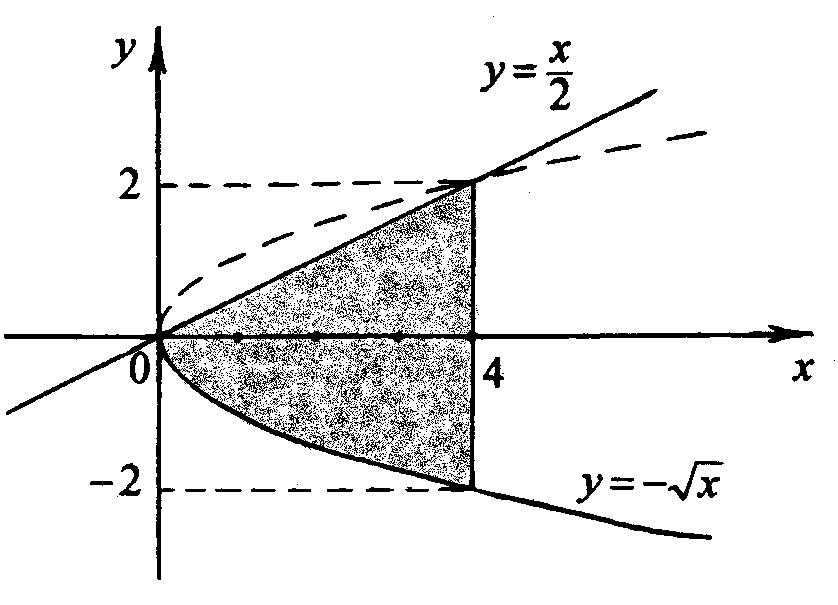
рис. 9

Выбирая внутреннее интегрирование по переменной , а внешнее по, получим:

Здесь внешний интеграл берется по переменной . Граничными точками этой переменной будут точкии, которые и определяют внешние пределы интегрирования. Внутренний интеграл берется по переменной. Пределы интегрирования для него будут являться функциями от, которые определяются из уравнений линий, ограничивающих областьD снизу () и сверху (). Следовательно,

Изменяя порядок интегрирования, разобьем область D на две части: пусть D₁ — часть, лежащая ниже оси , аD₂ — часть, лежащая выше оси . Тогда.

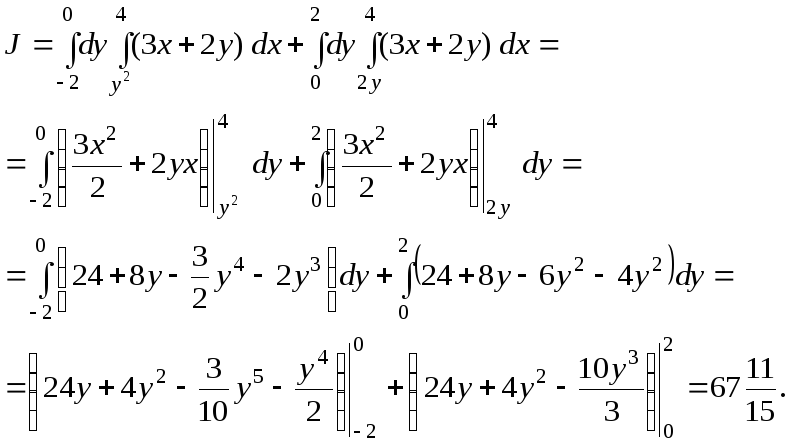
Совпадение результатов подтверждает правильность вычислений.

Вычисление двойного интеграла в полярной системе координат производится по формуле

или , (13)

где и— пределы изменения полярного углав областиD, а и—функции, задающие кривыеВNА и ВМА в полярной системе координат (рис.10), ограничивающие область D.

рис. 10

Площадь области D в декартовой системе координат, находится по формуле

.

Если область D в полярных координатах определена неравенствами , то

. (14)

Пример 2. С помощью двойного интеграла в полярных координатах найти площадь области, ограниченной линиями ,.

Решение. Уравнение можно привести к виду, которое определяет окружность радиуса 3 с центром в точкеА(3,0) (рис.11).

рис. 11

Учитывая, что декартовы и полярные координаты связаны формулами , запишем уравнения данной окружности и прямой в полярных координатах:

, или ;

, или , то есть.

Из рисунка 11 видно, что полярный радиус изменяется от 0 до значения r на окружности, то есть до , а угол изменяется от 0 до. Применяя формулу (14) получаем

3. Вычисление тройных интегралов

Пусть пространственная область V, по которой вычисляется тройной интеграл, ограничена снизу поверхностью , сверху — поверхностью, с боков — цилиндрической поверхностью с образующими, параллельными осиOZ. При этом область V проектируется на плоскость ОХУ в область D.

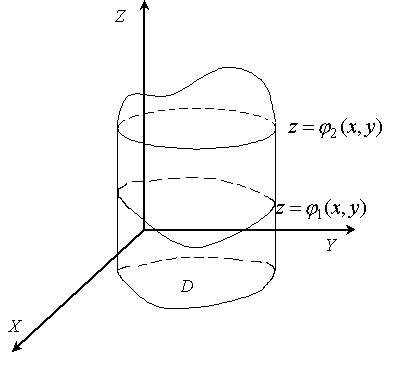
рис. 12

Тогда

(15)

Внутренний интеграл (в скобках) вычисляется по переменной z, при постоянных x и y, а внешний интеграл — это двойной интеграл по области D, вычислять который уже умеем.

Еще две аналогичные формулы можно получить при другом расположении области V относительно координатных плоскостей, вычисляя внутренние интегралы по x или y, а внешний — соответственно по y и z или x и z.

Пример 3. Найти массу тела, ограниченного поверхностями , если плотность распределения массы равна.

Решение. Уравнение определяет круговой цилиндр радиуса, с образующими,параллельными оси OZ. Уравнение определяет параболический цилиндр, с образующими,параллельными оси OZ. Уравнение определяет плоскость, проходящую через осьOX. Уравнение определяет плоскостьXOY.

Сделаем чертеж пространственной области V.

рис.13

Массу тела, ограниченного областью V с пространственной плотностью найдем по формуле

.

Так как , то.

Вычислим тройной интеграл

, где D — проекция области V на плоскость XOY, (рис 14).

рис.14

Найдем точки А и В пересечения кривых .

, следовательно, , откуда, причем— посторонний корень. Поэтому. Точки пересечения имеют координаты. Таким образом,

.

Вычислим двойной интеграл по области D