1.4. Интервалы монотонности и точки экстремума функции

Функция называетсявозрастающей (убывающей) в некотором интервале, если большому значению аргумента соответствует большее (меньшее) значение функции, т.е. при выполняется неравенство

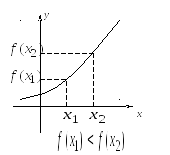
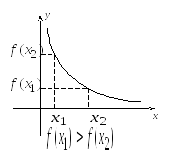
возрастает убывает

Признаки возрастания и убывания функции.

1. Если дифференцируемая функция 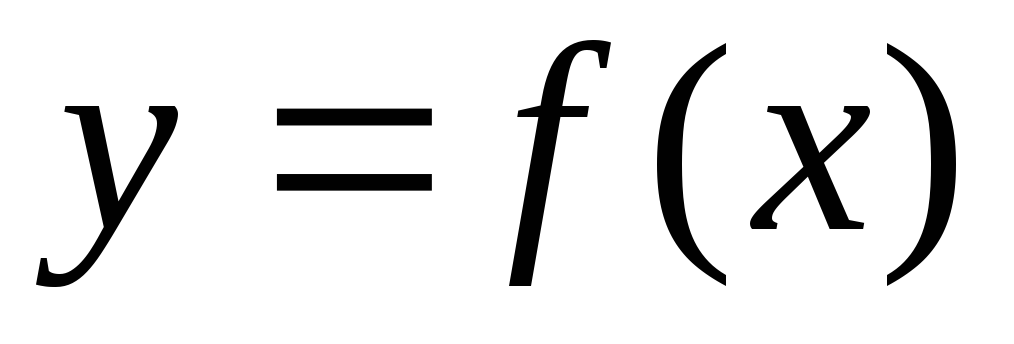на отрезке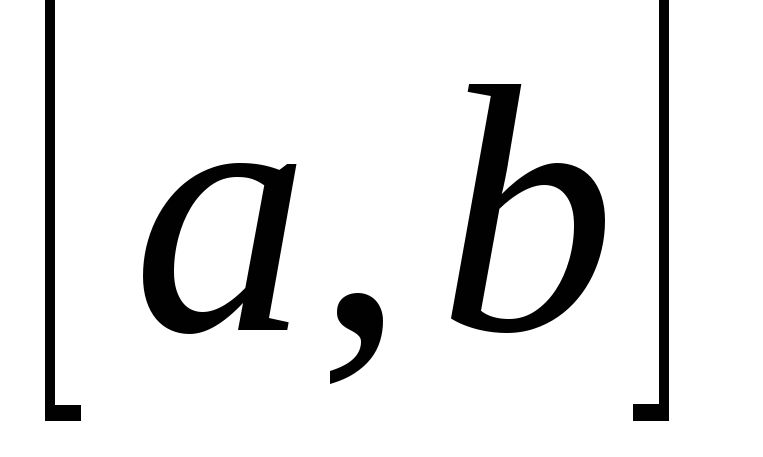возрастает (убывает), то ее производная на этом отрезке неотрицательна (неположительная) т.е..

2. Если непрерывна на 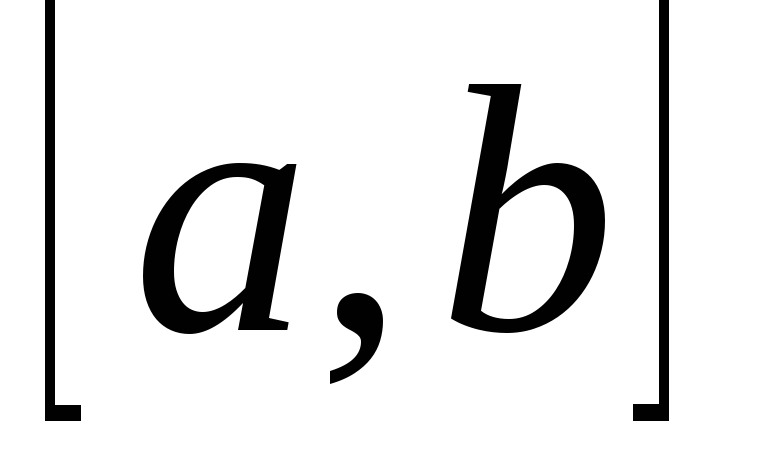и дифференцируется внутри него функция имеет положительную (отрицательную) производную, то она на этом отрезке возрастает (убывает).

Теорема 1.(необходимый признак локального экстремума).

Если функция имеет в точкеэкстремум, то либолибоне существует.

Точки, в которых производная обращается в нуль либо не существует, называются критическими точками. В них может быть экстремум, а может и не быть.

Теорема 2. ( первый достаточный признак локального экстремума).

Если при положительна, а приотрицательна то прифункцияимеет максимум. Если жепри отрицательна а приположительна, то прифункция имеет минимум.

Другими словами, если при переходе через критическую точку производная меняет знак, то это точка экстремума.

Пример. Исследовать на экстремумы функцию .

Решение. Данная функция определена и непрерывна, для всех . Находим её производную

.

Находим критические точки из условия и:

при т.е.,

при .

Эти точки разбивают область определения функции на интервалы , в каждом из которых производная функции сохраняет знак.

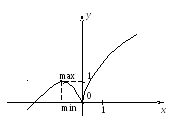
Достаточно определить знак производной в произвольной точке интервала. Имеем:

Значит точкаявляется точкой максимума и; точкаявляется точкой минимума и

Теорема 3. (второй достаточный признак локального экстремума).

Пусть функция дважды дифференцируема и. Тогда в точкеона имеет локальный минимум еслии локальный максимум если.

В случае, когда точкаможет и не быть экстремумом.

Пример. С помощь второй производной исследовать на экстремум функцию .

Решение. Находим и

Находим критические точки из условия или

.

Вычислим значение второй производной в этих точках

точка минимума,

точка максимума,

.

Задание 7.

Исследовать на экстремум функции

1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Нахождения наибольшего и наименьшего значения непрерывной функции на отрезке

На отрезке функцияможет достигать наименьшего() или наибольшего () значения либо в критических точках функции, лежащих в интервале (a;b), либо на концах отрезка .

Пример. Найти наибольшее и наименьшее значение функции на отрезке.

Решение. Производная этой функции

.

Найдем критические точки

Обе эти точки принадлежат интервалу . Вычисляем значение функции в критических точках и на концах отрезка:

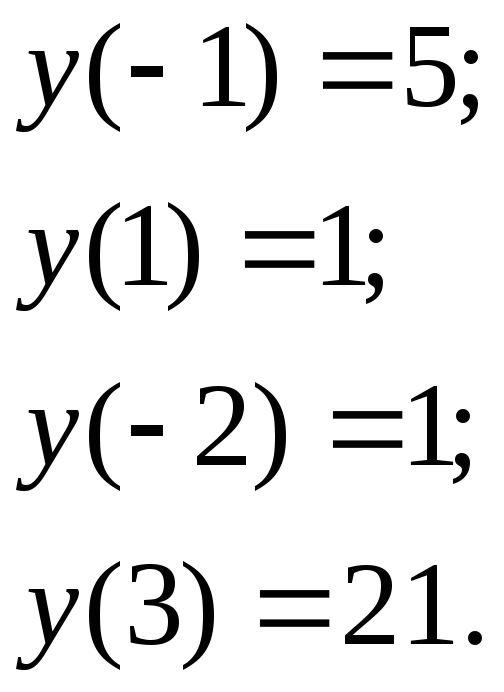
Сравнивая полученные числа, заключаем что

а .

Задание 8.

Найти наибольшее и наименьшее значение функции на заданном отрезке

1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30