Закон сохранения энергии

Полная механическая энергия системы – энергия механического движения и взаимодействия, равная сумме кинетической и потенциальной энергий .

Закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не меняется со временем

. (1.19)

Это фундаментальный закон природы. Он является следствием однородности времени – инвариантности физических законов относительно выбора начала отсчета времени.

Механические системы, на которые действуют только консервативные силы (внутренние и внешние), называются консервативными системами. В консервативных системах полная механическая энергия остается постоянной. Могут лишь происходить превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах, так что полная механическая энергия остается неизменной.

В системе, в которой кроме консервативных сил действуют и диссипативные силы, полная механическая энергия не сохраняется. Такие системы называются диссипативными. При «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида (например, тепловой). Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одной формы в другую. В этом заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.

Соударения

Удар (соударение) – столкновение дух или более тел, при котором взаимодействие длится очень короткое время.

Центральный удар – удар при котором тела до удара движутся по прямой, проходящей через их центры масс.

Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. При абсолютно упругом ударе сохраняются импульс и механическая энергия.

Рассмотрим прямой центральный абсолютно упругий удар двух шаров массами m₁ и m₂. Обозначим скорости шаров до удара и, после удара -и.

Рисунок 3 – Абсолютно упругое соударение шаров, двигающихся на встречу друг другу

Закон сохранения импульса в векторном виде:

. (1.20)

Закон сохранения энергии:

(1.21)

.

Отсюда

(1.22)

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.

Рисунок 4 – Абсолютно неупругое соударение шаров.

При абсолютно неупругом ударе выполняется только закон сохранения импульса:

. (1.23)

Или в проекциях на ось х:

₍₁₂₄₎

Скорость после удара равна:

(1.25)

Механическая энергия при неупругом ударе не сохраняется: вследствие деформации часть кинетической энергии переходит во внутреннюю энергию тел. Это уменьшение равно:

2 Вывод рабочей формулы

Используя баллистический метод, получим формулу для определения скорости шаров в момент прохождения положения равновесия.

В этом методе мерой скорости служит величина угла отброса, рассчитываемая по круглой шкале.

В точке А (рисунок 5) шарик обладает потенциальной энергией равной

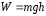_(2.1)

Систему маятник-Земля рассматриваем как замкнутую, пренебрегая трением в подвесе маятника и сопротивлением воздуха.

При перемещении шарика из положения А в положение С его потенциальная энергия перейдет в кинетическую.

_(2.2)

Рисунок 5 – Отклонение шарика от положения равновесия.

Откуда

_(2.3)

Используя соотношения в прямоугольном треугольнике и тригонометрическую формулу _, выразим высоту h через длину нити l и угол

_(2.4)

и подставим в выражение для скорости ( )

Получим

_(2.5)