
LABORATORNAYa_RABOTA_2_novaya
.pdfМинистерство образования Республики Беларусь Учреждение образования
«МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ»
Кафедра физики
ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Методические указания к лабораторной работе № 2 по разделу "Механика и молекулярная физика" курса общей физики
для студентов всех специальностей дневной и заочной формы обучения
Могилев 2010
1

Рассмотрены и рекомендованы к изданию
на заседании кафедры физики Протокол № 9 от 28 июня 2010 г.
Составители:
ст. преподаватель Забиран Т.В., ассистент Пусовская Т.И.
Рецензент:
кандидат физико математических наук, доцент УО МГУП В.Л.Малышев.
УДК 532.516 ©УО «Могилевский государственный
университет продовольствия», 2010
2

ЛАБОРАТОРНАЯ РАБОТА № 2
ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА
ЦЕЛЬ РАБОТЫ: изучение колебательного движения, видов маятников, особенностей свободного падения, измерение ускорения свободного падения с помощью математического маятника.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: математический маятник,
секундомер.
1 ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
1.1 Гармонические колебания
Колебаниями называются движения или процессы, которые обладают повторяемостью во времени. Колебания сопровождаются попеременными превращениями энергии одного вида в энергию другого вида. Колебательные движения, как простые, так и сложные, широко распространены в технике: движение поршня двигателей, годичное изменение температуры воздуха, биение сердца человека и животных и др. Колебания называются периодическими, если система за равные промежутки времени возвращается в положение равновесия.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии, без дальнейшего внешнего воздействия на колебательную систему (систему, совершающую колебания). Колебания называются вынужденными, если они происходят под действием периодически повторяющейся внешней силы.
Гармоническими колебаниями называются колебания, происходящие под действием упругой или квазиупругой силы, и колеблющаяся физическая величина изменяется по закону синуса или косинуса.
Квазиупругой (подобной упругой) силой называется любая сила, возвращающая систему в положение равновесия и пропорциональная смещению.
Уравнение гармонических колебаний имеет вид:
|
x |
A sin ( |
t |
0 ) , |
(1) |
или |
|
|
|
|
|
|
x |
A cos ( |
t |
0 ) , |
(2) |
где |
x – смещение колеблющейся точки, |
|
|||
A – амплитуда (наибольшее смещение материальной точки от положения равновесия),
( t 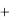 0 ) – фаза гармонического колебания,
0 ) – фаза гармонического колебания,
0 – начальная фаза (угловая мера, определяющая смещение материальной точки в начальный момент времени),
3

– циклическая (круговая) частота гармонического колебания.
Периодом колебаний T называют наименьший промежуток времени, за который совершается одно полное колебание (система возвращается в исходное положение).
Частотой колебаний 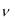 называется величина обратная периоду колебаний T1 , т.е. число полных колебаний, совершаемых в единицу времени.
называется величина обратная периоду колебаний T1 , т.е. число полных колебаний, совершаемых в единицу времени.
1.2 Маятники
Маятники под действием силы тяжести также совершают гармонические колебания, если углы отклонения от положения равновесия малы. Маятники бывают: математический, физический и пружинный.
Пружинный маятник – это тело массой т, подвешенное на абсолютно
упругой пружине и совершающий колебания под действием упругой силы. |
|
Fупр. kx, |
(3) |
где k – жесткость пружины (коэффициент упругости).
|
0 |
|
|
|
Fупр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
mg |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Рисунок 1 – Пружинный маятник |
|
||||||||||||||||||
Уравнение движения маятника: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
mx |
kx или |
x |
k |
x 0 . |
(4) |
|||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
Сравнивая это уравнение с уравнением движения гармонического |
||||||||||||||||||||
осциллятора x |
2 x 0 , мы видим, что пружинный маятник совершает колебания |
|||||||||||||||||||
по закону |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
A cos( |
t |
0 ) , |
|
|||||||||||||
с циклической частотой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
(5) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и периодом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
T |
2 |
|
|
|
|
|
m |
|
|
(6) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
k . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||

Физическим маятником называют твердое тело, имеющее неподвижную ось вращения, проходящую через точку, не совпадающую с его центром масс, и совершающее колебания под действием силы тяжести. Период T малых колебаний (угол отклонения от положения равновесия равен 3-5о) физического маятника не зависит от амплитуды и определяется по формуле
|
|
|
I |
|
|||
T 2 |
|
|
|
, |
|
(7) |
|
|
mgd |
||||||
где I – момент инерции маятника относительно оси вращения, |
|
||||||
m – его масса, |
|
|
|
|
|
|
|
d – расстояние от оси вращения до центра инерции, |
|
||||||
g – ускорение свободного падения |
|
|
|
|
|
|
|
Величину |
|
|
|
|
|
|
|
|
L |
|
I |
(8) |
|||
|
|
|
|
|
|||
|
|
md |
|||||
|
|
|
|
|
|||
называют приведенной длиной физического маятника. Таким образом,
период колебаний физического маятника можно записать в виде
T 2 |
L |
(9) |
||
|
|
|||
g . |
||||
|
|
|||
Частным случаем физического маятника является математический маятник. Математическим маятником называется идеализированная система, представляющая собой материальную точку, подвешенную на невесомой и нерастяжимой нити и совершающую колебания под действием силы тяжести. Выведем формулу периода колебаний математического маятника.
 О
О
α
l
F
С x
mg 
Рисунок 2 – Математический маятник
Отклоним маятник из положения равновесия на некоторый угол α и определим действующую при этом на маятник силу. Сила, действующая на маятник, равна mg, где m – масса маятника и g – ускорение силы тяжести (ускорение свободного падения). Эту силу мы разложим на две составляющие (рис.2): одну вдоль нити и другую перпендикулярно нити. Первая составляющая
5
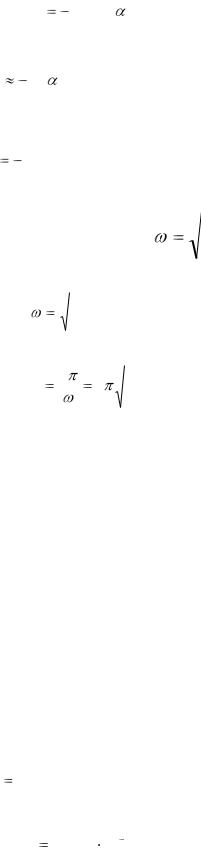
компенсируется натяжением нити, а вторая вызывает движение маятника. Эта составляющая равна очевидно,
|
F mg sin |
. |
|
|
(10) |
|||
|
|
|
|
|
|
|||
В случае малых колебаний угол α мал. При этом sin α |
приближенно равен |
|||||||
самому углу α, так что |
|
|
|
|
|
|
|
|
F |
mg |
. |
|
|
|
(11) |
||
|
|
|
|
|
|
|||
Замечая, что lα (где l –длина маятника) представляет собой путь x, |
||||||||
пройденный материальной точкой, запишем F в виде |
|
|
|
|
|
|||
F |
mg |
x |
|
|
|
|
|
|
|
|
|
|
|
(12) |
|||
|
l . |
|
|
|
||||
|
|
|
|
|
|
|||
Отсюда видно, что коэффициент жесткости в случае малых колебаний |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
маятника k=mg/l. Частота гармонических колебаний |
|
|
поэтому частота |
|||||
m |
|
|||||||
|
|
|
|
|
|
|
, |
|
колебаний математического маятника будет |
|
|
|
|
|
|
||
|
|
|
g |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l . |
|
|
|
||||
Период колебаний маятника равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
2 |
|
2 |
|
l |
||||
|
|
|
|
|
|
|
||||
|
|
|
g , |
|||||||
|
|
|
|
|
|
|
|
|||
где |
l – длина маятника, |
|
|
|
|
|
|
|
|
|
g – ускорение свободного падения. |
|
|
|
|
|
|
|
|
|
|
(13)
(14)
1.3Свободное падение
Под действием силы тяжести всякое тело падает на Землю с ускорением g –
ускорением свободного падения.
Движение называют свободным, когда его траектория и скорость ничем не ограничиваются. Свободным падением будет движение тела в безвоздушном пространстве (вакууме) под действием силы тяжести.
Ускорение g определяется только полем земного тяготения в данной точке, поэтому оно не зависит от формы, размеров, массы тела, его скорости.
Поскольку на разных географических широтах сила тяжести одного и того же тела разная, то ускорение свободного падения g меняется в зависимости от широты места. На полюсах, где линейная скорость вращения точек Земли равна нулю, сила тяжести mg максимальна и равна силе притяжения F
F G |
m M |
з |
|
|
|
Rз 2 |
, |
(15) |
|||
|
|||||
|
|
||||
где Мз, Rз – масса и радиус Земли соответственно, |
|||||
G – гравитационная постоянная ( G 6,6720 10 11 |
м3 / с2 кг ). |
||||
На полюсе ускорение свободного падения g=9,832 м/ с2. На экваторе сила тяжести принимает минимальное значение и ускорение свободного падения g=9,781 м/ с2. Так как Земля имеет не сферическую форму, а «сплюснута» у
6
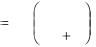
полюсов, то это также приводит к различию значений g на экваторе и полюсах. Значение g для разных широт определено экспериментально. Ускорение свободного падения на широте φ=45о называется нормальным и равно 9,807м/с2. Так как различие значений g невелико, при решении практических задач ускорение свободного падения принимается равным 9,81 м/с2.
Все перечисленные значения ускорения свободного падения относятся к определению этой величины на уровне моря. Из равенства инертной массы тела, которая входит во второй закон Ньютона, и его гравитационной массы в законе Всемирного тяготения следует, что с увеличением высоты подъема над уровнем моря ускорение свободного падения изменяется по закону
|
|
Rз |
|
2 |
|
g g |
|
|
|
|
|
0 |
Rз |
h |
|
|
|
|
|
, |
(16) |
||
|
|
|
|
где g−ускорение свободного падения на высоте h над уровнем моря, go− на уровне моря.
Для примера приведены значения ускорения свободного падения для некоторых городов (географические координаты по Гринвичу).
Таблица 1 – Значения ускорения свободного падения для различных географических точек
|
|
|
Высота |
Ускорение |
|
Город |
Долгота |
Широта |
над |
свободного |
|
уровнем |
падения, |
||||
|
|
|
|||
|
|
|
моря, м |
м/с2 |
|
Берлин |
13,40 в.д. |
52,50 с.ш. |
40 |
9,81280 |
|
Будапешт |
19,06 в.д. |
47,48 с.ш. |
108 |
9,80852 |
|
Вашингтон |
77,01 з.д. |
38,89 с.ш. |
14 |
9,80112 |
|
Вена |
16,36 в.д. |
48,21 с.ш. |
183 |
9,80860 |
|
Гринвич |
0,0 в.д. |
51,48 с.ш. |
48 |
9,81188 |
|
Каир |
31,28 в.д. |
30,07 с.ш. |
30 |
9,79317 |
|
Киев |
30,30 в.д. |
50,27 с.ш. |
179 |
9,81054 |
|
Мадрид |
3,69 в.д. |
40,41 с.ш. |
655 |
9,79981 |
|
Москва |
37,61в.д. |
55,75 с.ш. |
151 |
9,8154 |
|
Нью-Йорк |
73,96 з.д. |
40,81 с.ш. |
38 |
9,80247 |
|
Одесса |
30,73 в.д. |
46,47 с.ш. |
54 |
9,80735 |
|
Осло |
10,72 в.д. |
59,91 с.ш. |
28 |
9,81927 |
|
Париж |
2,34 в.д. |
48,84 с.ш. |
61 |
9,80943 |
|
Прага |
14,39 в.д. |
50,09 с.ш. |
297 |
9,81014 |
|
Рим |
12,99 в.д. |
41,54 с.ш. |
37 |
9,80312 |
|
Стокгольм |
18,06 в.д. |
59,34 с.ш. |
45 |
9,81843 |
|
Токио |
139,80 в.д. |
35,71 с.ш. |
18 |
9,79801 |
7

Можно сделать окончательный вывод: ускорение свободного падения
зависит от широты местности, высоты над уровнем моря и от плотности залегающих пород.
2 ОБОСНОВАНИЕ МЕТОДИКИ ЭКСПЕРИМЕНТА
Из формулы (14) следует, что для определения ускорения свободного падения необходимо знать период колебаний математического маятника Т и его длину l, определение которой в лабораторных условиях не всегда возможно. Поэтому в экспериментальной установке используют нить (трос) с изменяющейся длиной. В качестве материальной точки применяют тело, формой и размерами которого в рассматриваемых условиях можно пренебречь (его диаметр много меньше длины подвеса). Определяем период колебаний математического маятника Т1 при длине l1, а затем изменяем длину нити и определяем новый период колебаний маятника Т2 при длине l2. Получим
T1 |
2 |
|
|
|
l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
g |
, |
|
|
|
|
|
|
|
(17) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
T2 |
2 |
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
g |
. |
|
|
|
|
(18) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Возведем Т2 и Т1 в квадрат и вычтем Т1 из Т2 |
.Получим |
|
|||||||||||||||||||
T |
2 |
T 2 |
4 |
2 |
|
|
|
l2 |
l1 |
|
|
|
|||||||||
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(19) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g 4 2 |
l2 |
l1 |
|
|
|
|
|
|
4 |
|
|
2 |
|
|
l |
|
|
|
|||
T 2 |
T |
2 |
|
|
|
|
|
|
|
|
|
T |
2 T |
2 |
|
(20) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
1 |
. |
||||||
Применим эту формулу в лабораторной работе. Из нее следует, что для опытного определения ускорения свободного падения достаточно экспериментально найти изменение длины маятника ∆l и периоды колебаний Т1 и
Т2.
3ОПИСАНИЕ УСТАНОВКИ
ИПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Лабораторная установка состоит из стальной проволоки, длину которой можно менять, и подвешенного на ней чугунного шара. Проволока вверху переброшена через блок и вторым концом прикреплена к указателю, который может, если отвинтить винт, передвигаться вдоль шкалы h с сантиметровыми делениями. Чтобы изменять длину l маятника, следует перемещать его вдоль шкалы. Для этого поступают следующим образом: один студент двумя руками поддерживает шар и слегка приподнимает его, а второй отвинчивает винт на указателе и перемещает его вдоль шкалы. И только, когда он закрепит винт в нужном положении, первый студент постепенно отпускает шар.
8

2.Зафиксировав указатель в положении h1 ближе к нижнему пределу шкалы, запишите его. При этом длина маятника примет значение равное l1.
3.Отклоните маятник на 3о-5о и отпустите его. При малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону. Пропустив 3-4 полных колебания, включите секундомер,
иопределите время t1 ' двадцати полных колебаний (n=20). Затем повторите эту
операцию дважды, определите t1", t1" и найдите t1 ср
t1ср |
t1 t1 |
t1 |
|
|
|
3 |
. |
(21) |
|||
|
|||||
Определите период колебаний Т1
T1 |
t1 ср |
|
|
n . |
(22) |
||
|
4.Обращаясь с маятником так, как описано в пункте 1, измените длину маятника не менее чем на 60см. Зафиксируйте указатель винтом и запишите
значение шкалы h2, на уровне которого он находится. При этом длина маятника примет соответствующее значение l2.
5.Повторите действия пункта 3. Определите соответственно t2 ср и период
колебаний маятника Т2.
6.По формуле (20) рассчитайте ускорение свободного падения g1, учитывая, что ∆l=h2-h1 соответствует изменению длины маятника.
7.Повторите действия пунктов 1-5 еще для двух разных длин маятника и рассчитайте g2 и g3. Определите среднее значение g.
8.Сравните полученное значение g с табличным значением (g0=9,81м/с2) и рассчитайте относительную погрешность по формуле:
g0 |
g |
100% |
|
|
|
g0 |
|
|
|
(23) |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое движение называется колебательным?
2.Какие колебания называются периодическими, свободными, вынужденными?
3. Какие колебания называются гармоническими?
4. Уравнение гармонического колебания и его параметры (амплитуда, смещение, начальная фаза, период, частота).
5. Какая сила называется квазиупругой?
6. В чем состоит различие между маятниками: физическим, математическим и пружинным?
7. Как определить периоды колебаний физического и пружинного маятников?
8. От каких величин зависит приведенная длина физического маятника?
9

9. Выведите формулу периода колебаний математического маятника.
10. Какое движение называется свободным?
11. Сформулируйте закон Всемирного тяготения. Каков физический смысл гравитационной постоянной?
12. Что такое ускорение свободного падения?
13. От чего зависит ускорение свободного падения?
14. Как изменяется ускорение свободного падения с увеличением подъема над поверхностью Земли?
ЛИТЕРАТУРА
1.Савельев, И.В. Курс общей физики. Т. 2 / И.В.Савельев. – 3-е изд. – М.: Наука, 1988.
2.Детлаф, А.А. Курс физики / А.А.Детлаф, Б.М.Яворский. – 5-е изд. – М.: Академия, 2005.
3.Трофимова, Т.И. Курс физики. М.: ВШ, 2007.
10
