
MATLAB00 / Mironovskiy_Petrova1ML_ВЫЧ
.pdf
|
1 |
C |
|
2 |
|
3 |
CA |
|
4 |
R 5 [B, AB, ..., An 1B], D 5 |
3 |
|
4. |
|
|
3 ... |
|
4 |
|
|
3 |
|
|
4 |
|
3CAn |
1 |
4 |
|
|
6 |
|
|
7 |
Приведем соответствующие критерии.
Критерий управляемости. Для того чтобы система была управ ляемой необходимо и достаточно, чтобы матрица управляемости имела полный ранг: rankR = n.
Критерий наблюдаемости. Для того чтобы система была наблю даемой необходимо и достаточно, чтобы матрица наблюдаемости имела полный ранг: rankD = n.
Критерий минимальности. Для того чтобы система была мини мальной необходимо и достаточно, чтобы обе матрицы R и D имели полный ранг: rankR = n, rankD = n.
Формирование матриц управляемости и наблюдаемости произво дится с помощью команд ctrb и obsv (от controlability и observability). Их синтаксис одинаков: R=ctrb(sys), D=obsv(sys). В качестве аргумен тов можно использовать непосредственно матрицы A, B, C описания в пространстве состояний, например R=ctrb(A, B), D=obsv(A, C) или
R=ctrb(sys.a, sys.b), D=obsv(sys.a, sys.c). Для вычисления ранга этих матриц используется команда rank.
Другой способ проверки управляемости и наблюдаемости опира ется на вычисление рангов так называемых грамианов управляемос ти и наблюдаемости. Для их нахождения служит команда gram, до полнительные сведения о ней можно найти в подразд. 4.4, 4.5.
Если система неуправляема или ненаблюдаема, то ее порядок мо жет быть понижен путем удаления неуправляемых и ненаблюдае мых подсистем. У SISO систем это эквивалентно сокращению совпа дающих нулей и полюсов передаточной функции. Для этой цели ис пользуется команда minreal (от minimal realization).
Ее можно использовать с одним и двумя входными аргументами: sys1=minreal(sys) и sys1=minreal(sys, eps). Второй аргумент позволяет указывать допуск , задающий степень близости сокращаемых ну лей и полюсов.
Пример 2 (анализ минимальности). Рассмотрим систему с переда
2 p 11
точной функцией Q( p) p2 1 3p 1 2. Она имеет один нуль z1= –1 и два
полюса р1= – 1, р2= – 2. Система неминимальна, поскольку р1= z1. Сформируем tf модель этой системы и найдем ее нули и полюсы:
41
>>s=tf([1 1],[1 3 2]) |
>>zero(s) |
>>pole(s) |
>>eig(s) |
>>[p, z]=pzmap(s) |
s + 1 |
1 |
2 |
2 |
p = 2 z = 1 |
—————— |
1 |
1 |
1 |
|
s2 + 3 s + 2 |
|
|
|
|
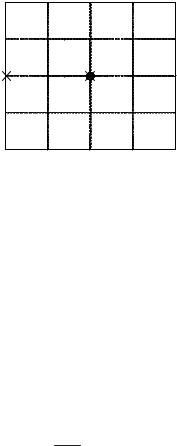
Расположениенулейиполюсовнакомплекснойплоскостиможнопо лучить,набравкомандуpzmap(s) безвыходногоаргумента(нарис.2.7 по люсы помечены крестиками, нуль – ноликом).
6789 9 7
2
5 534
9
8
7
365 5
4
3
211534
12 11 |
1234 |
12 |
1534 |
5 |
9 8
Рис. 2.7
Оба полюса отрицательны, следовательно, система устойчива. Наличие диполя (совпадающего нуля и полюса) в точке (–1, 0) гово рит о неминимальности системы.
Перейдем к ss модели и проанализируем ее управляемость и на блюдаемость, используя команды ctrb, obsv и rank:
>>s1=ss(s) |
>>R=ctrb(s1) |
>>D=obsv(s1) |
>>rank(R) |
>>rank(D) |
||
a = 3 2 b = 2 |
|
R = 2 6 |
D = 0.5 0.5 |
|
|
|
1 0 |
0 c = 0.5 0.5 |
0 2 |
1 1 |
2 |
1 |
|
нижен.
q=minreal(s), получаем ответ q 1 1 |
. К тому же результату прихо |
s 2 |
2 |
Анализируя ранги матриц R и D, заключаем, что система s1 управ |
|
ляема, но ненаблюдаема, следовательно, ее порядок может быть по |
|
Найдем передаточную функцию минимальной реализации:
дим,сокращаячислительизнаменательисходнойпередаточнойфунк ции Q( p) на общий множитель р+1.
42
Заметим, что статический коэффициент усиления при переходе к минимальнойреализациинеизменился:
>>K=dcgain(s) |
>>k=dcgain(q) |
K=0.5 |
k=0.5 |
Весовая и переходная функции также остаются прежними. В этом можно убедиться с помощью команд impulse(s, q), step(s, q), по которым будут построены графики указанных функций для обеих систем.
Командыctrb и obsv можноиспользоватьприработессимвольными выражениями,например,когдачастьэлементовматрицA,b,cзаданыв буквенномвиде.
Пример 3 (анализ управляемости и наблюдаемости системы третье гопорядка).Объектуправлениязаданописаниемвпространствесосто яний
|
4 |
3a |
1 |
0 5 |
|
|
4a |
5 |
|
|
|
1 |
6 |
1 |
3a2 |
7 |
, |
b 8 |
6 |
2 |
7 |
, c 8 |
11 1 12 , |
X = AX + bu, y = cX, A 8 |
6 |
0 |
0 7 |
6a3 7 |
|||||||
|
96 |
0 |
1 |
3a1 7 |
|
|
96 1 7 |
|
|
||
где X R3 – вектор состояний, u, y – входной и выходной сигналы. Требуется проанализировать его управляемость и наблюдаемость. Решение. Вводим исходные символьные матрицы:
>>syms a1 a2 a3 real
>>A=[ a1 1 0;0 –a2 0;0 1 a1]; b=[a2;a3;1]; с=[1 1 1];
Формируем матрицы управляемости и наблюдаемости
R=[b, Ab, A2b], D = [cT, (cA)T, (cA2)T]T:
|
>> R=ctrb(A, b) |
|
>> D=obsv(A, c), |
|
|
[a2, |
a1*a2+a3, |
a1*( a1*a2+a3) a2*a3] |
[1, |
1, |
1] |
[a3, |
a2*a3, |
a2^2*a3 ] |
[ a1, |
2 a2, |
a1] |
[1, |
a3 a1, |
a2*a3 a1*(a3 a1)] |
[a1^2, |
2*a1 (2 a2)*a2, |
a1^2] |
Вычисляем определители: det(R)=0, det(D)=0. Оба определителя рав ны нулю, следовательно, система неуправляема и ненаблюдаема.
Вырожденностьматрицынаблюдаемостиочевидна(еепервыйитре тий столбцы совпадают). Вырожденность матрицы управляемости «на глаз» обнаружить значительно сложнее.
Задачи и упражнения
1. Для приведенных ниже систем второго порядка найти диффе ренциальное уравнение, передаточную функцию, весовую функцию, описание в пространстве состояний и выполнить моделирование в MATLAB.
43

а. Механическая система с трением.
1 |
3 |
112134554 6789412 |
1 |
3121 5 5 7812 |
|
|
2 1 21 1 7 |
|
|
|
21234 145215 41 7 |
Входной сигнал – сила F, выход – координата x или скорость
1 2 x1.
б. Электрическая схема (параллельный колебательный контур).
1 |
5 |
2 6 2 |
1 |
2 |
3 2 |
4 |
2 |
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
1 1 2 |
1 2 |
1 3 |
||
в.Электрическаясхема(последовательныйколебательныйконтур).
11
|
|
2 1 |
|
12 |
3 1 |
4 1 |
12 |
5 1
6 1
Численные значения параметров L, mпринять равными числу букв в Вашей фамилии; R, – числу букв в имени/10; с, k – числу букв в отчестве.
Указание. При построении математической модели использовать уравнения:
44

второй закон Ньютона
ma 1 2v 1 kx 3 F,
где v 1 x1, a 1 x11;
законы Кирхгофа и Ома
i 1 i 1 i 2 i(t), |
u 1 u 1 u 2 u, |
i 2 u/z( p), z 2 R, |
z 2 |
1 |
, z 2 Lp. |
|
|||||
L C R |
L c R |
R |
C |
Cp |
L |
|
|
|
|
|
2. Используя команду dsolve, найти решение дифференциального уравнения
111x 1 x11 1 x1 1 x 2 0,
сначальнымиусловиями: a) x0 1 x110 11, x10 1 22; б)x0 1 60, x10 1 x110 1 0.
Ответ: а) x 1 e t 2 sint ,
б) x 1 30(e t 2 sint 2 cost) 1 30e t 1 42,4sin(t 1 45o ) .
3. Решить в символьном виде следующие дифференциальные урав нения:
а) 111x 1 2x11 2 x1 3 4, x(0) 3 1, x1(0) 3 2, x11(0) 3 12; б) x11 1 n2x 2 asin(nt 1 3), x(0) 2 x1(0) 2 0.
Ответ: а) x(t) 1 4t 2 3 3 2et,
б) x(t) 3 a 1sin nt cos4 5 nt cos(nt 6 4)2. 2n2
4. Найти реакцию апериодического звена с передаточной функци
ей Q( p) 1 |
1 |
на входной сигнал u 1 e12t , 0 t T. Определить мак |
|
||
|
p 2 a |
|
симум выходного сигнала. Выполнить численное и символьное моде лирование в MATLAB, приняв a = 1; b = 2; T = 3.
Решение.
а. Программа моделирования в MATLAB (тулбокс CONTROL):
a = 1; b = 2; T = 3; |
% Задание параметров |
t = linspace(0, T); u = exp( b*t); |
% Входной сигнал |
sys = tf(1, [1 a]); |
% Описание системы |
y = lsim(sys, u, t); |
% Моделирование |
ym = max(y); plot(t, y). |
% Вывод результатов |
б. Аналитическое решение (тулбокс SYMBOLIC);
45

y(t) 3 5 14 a 1e at 4 e 2t 2.
При 1 2 a (особый случай) решение принимает вид
y( p) 1 |
1 |
; |
y(t) 1 te at. |
|
( p 2 a)2 |
||||
|
|
|
При этом tM = 1/a, y(tM) = 1/ae.
5. Дано дифференциальное уравнение y(4) – y = e–t с начальными
условиями: y 1 3, |
y1 |
1 25.25, y11 |
17.5, |
111y 1 25.75. |
Найти аналити |
0 |
0 |
0 |
|
0 |
|
ческое решение в MATLAB. Рассмотреть три варианта численного моделирования и сравнить их по точности.
Возможная техническая интерпретация задачи – управление не устойчивым объектом, считая у отклонением, а u = e–t – управле нием.
Ответ: Аналитическое решение исходного уравнения: y 1 (5 2 0,25t)e t 22cost .
Отметим, что в решение не вошла неустойчивая мода C1et. Это означает, что программное управление e–t обеспечивает колебатель ное движение объекта около неустойчивого положения равновесия. На практике неизбежно появление малых отклонений, которые со временем будут лавинообразно нарастать.
Три варианта численного моделирования
а. Раздельная реализация управления и системы.
|
3 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
9 9 6 68181818 6 89 99 9 9 |
|
|
|
|
|
|
|
61 8 1 6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 7 |
6 |
|
|
|
|
|
|
9 9 1 |
|
|
|
|
|
|
|
! "3 # 2#$%9 |
1 |
|
|
|
|
|
|
% ! &' (8 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
8 |
|
1 |
2 |
3 |
4 |
5 |
61 |
|
|
|
Компьютер выдает правильное решение при Т< 8 с, далее машин ное решение «разваливается».
б. Совместная реализация управления и системы. Входной сигнал
46

u = e–t формируется с помощью апериодического звена, в качестве вектора b используется вектор Х0. Общий порядок системы равен 5. Ранг матрицы управляемости R 1 [b,Ab,...,A4b] равен 4, т. е. реали зация неминимальна. Тем не менее теперь правильное решение со храняется втрое дольше (на интервале 25 с.).
в. Дальнейшего увеличения точности решения можно достичь, если выполнить редукцию и перейти к минимальной реализации 4 го порядка. В пакете MATLAB такая редукция выполняется с помо щью команды minreal. Аналитически редукцию можно выполнить, вычислив передаточную функцию
Q( p) 3 15,75p4 21,75p3 2 2,25p2 12,25p 2 4 ( p 21)( p4 11)
и затем сократив числитель и знаменатель на общий множитель р–1.
47
