2.6.5. Признак переполнения разрядной сетки
При алгебраическом суммировании двух чисел, помещающихся в разрядную сетку, может возникнуть переполнение, т.е. образуется сумма, требующая для своего представления на один двоичный разряд больше, чем разрядная сетка слагаемых. Предполагается, что положительные числа представляются в прямом коде, а отрицательные в дополнительном.
Признаком переполнения является наличие переноса в знаковый разряд суммы при отсутствии переноса из знакового разряда (положительное переполнение) или наличие переноса из знакового разряда суммы при отсутствии переноса в знаковый разряд (отрицательное переполнение).
При положительном переполнении результат операции положительный, а при отрицательном переполнении – отрицательный.
Если и в знаковый, и из знакового разряда суммы есть переносы или этих переносов нет, то переполнение отсутствует.
Рассмотрим простейшие примеры с трехбитовыми словами. Диапазон чисел, которые они представляют, равен от -4 до +3. В рассматриваемых словах 1 бит знака и 2 информационных бита.
1. Алгебраическое суммирование без переноса.
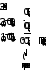
Поскольку перенос в знаковый разряд или из знакового разряда суммы отсутствует, то переполнения нет.
Результат – положительное число в ПК, равное 3.
2. Алгебраическое суммирование с двумя переносами.
Имеются переносы в знаковый разряд и из знакового разряда вычисляемой суммы, поэтому переполнения нет.
Результат – отрицательное число в ДК, равное -4.
3. Алгебраическое суммирование с одним переносом.
(Положительное переполнение).
При суммировании есть перенос в знаковый разряд суммы, а перенос из знакового разряда отсутствует, т.е. имеет место положительное переполнение, и результат операции положительный.
Число 4 нельзя представить в прямом коде. Формальный результат равен -4.
4. Алгебраическое суммирование с одним переносом.
(Отрицательное переполнение).
Число -5 нельзя представить 3-битовой комбинацией. Формальный результат равен +3.
Из рассмотренных ранее примеров видно, что арифметические операции в дополнительном коде выполняются достаточно просто. Необходимо только не упускать из виду то, с какими числами происходит работа в данный момент – без знака или со знаком. Поскольку внешний вид обоих чисел одинаков, возможны ошибки.
2.6.6. Деление в дополнительном коде
Деление в дополнительном коде осуществляется по тем же правилам, что были описаны в п. 5.4. разд. "Двоичная арифметика". Но метод деления "столбиком" для ЭВМ не пригоден. Используются более громоздкие методы деления, которые здесь не рассматриваются. Информацию о них можно найти в литературе, приведенной в конце главы.
2.6.7. Правило перевода из дополнительного кода в десятичную систему
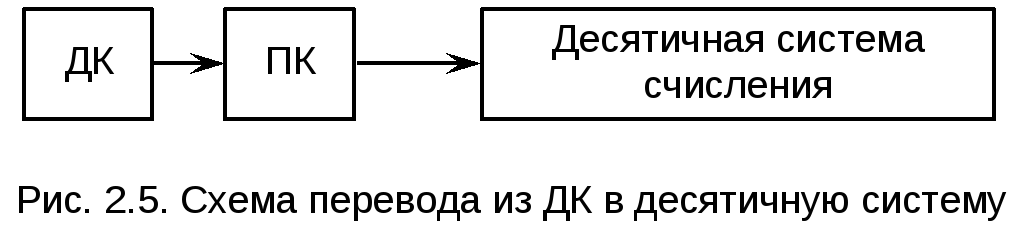
Перевод чисел из дополнительного кода в десятичную систему можно проводить по схеме, приведенной на рис. 2.5.
Однако существует прямой способ перевода числа из ДК в десятичную систему без использования промежуточного перевода в ПК.
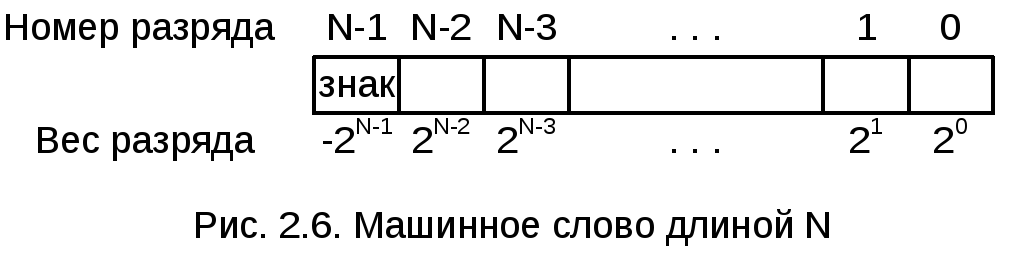
Рассмотрим машинное слово произвольной длины (рис. 2.6). При прямом способе перевода десятичное число со знаком формируется как сумма разрядов со своими весами и знаками (старший N-й разряд имеет отрицательный вес).
Проиллюстрируем перевод чисел из ДК в десятичную систему примерами.
Пример.
Перевести число 1110 из ДК в десятичную систему.
Проверим правильность перевода, используя промежуточный перевод в ПК:
Пример.
Перевести число 101100 из ДК в десятичную систему.
101100(2)(ДК) = -25+23+22= -32+8+4 = -20(10)
Проверим:
