Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет приборостроения и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дом_зад_Матлаб_02.doc

Скачиваний:

107

Добавлен:

09.04.2015

Размер:

1.58 Mб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

2.5 Аппроксимация и интерполяция данных При аппроксимации и интерполяция данных в Matlab применяются следующие основные методы:

icubic - кубическая интерполяция функции одной переменной;

spline - интерполяция функции одной переменной кубическим сплайном;

interp1 - одномерная табличная интерполяция;

interp2 - двумерная табличная интерполяция;

interpft - аппроксимация периодической функции на основе быстрого преобразования Фурье.

Эти методы применимы для табличных данных и функций, в последнем случае таблица данных вычисляется.

2.5.1 Кубическая интерполяция функции одной переменной icubic

Синтаксис:

yi = icubic(y, xi) yi = icubic(x, y, xi)

Описание:

Функция yi = icubic(y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические полиномы. Если Y - двумерный массив, то интерполирующая кривая строится для каждого столбца. Если указано значение xi вне области определения функции, то результатом будет NaN.

Функция yi = icubic(x, y, xi) позволяет использовать более мелкую сетку xi при условии, что аргумент x изменяется монотонно и сетка равномерна.

Пример:

Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.

x = 0:10; y = sin(x); xi = 0:.25:10; yi = icubic(x, y, xi); plot(x, y, 'o', xi, yi, ‘g’), grid.

Результат кубической интерполяции представлен на рисунке 8

Рисунок 8 - Результат кубической интерполяции

2.5.2 Интерполяция функции одной переменной кубическим сплайном spline

Синтаксис:

yi = spline(x, y, xi)

pp = spline(x, y)

v = ppval(pp, xx)

[breaks, coefs, l, k] = unmkpp(pp)

pp = mkpp(breaks, coefs)

Описание:

Функция yi = spline(x, y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические сплайны.

Функция pp = spline(x, y) возвращает pp-форму сплайна, используемую в m-файлах ppval, mkpp, unmkpp. Функция v = ppval(pp, xx) вычисляет значение кусочно-гладкого полинома pp для значений аргумента xx.

Функция [breaks, coefs, l, k] = unmkpp(pp) возвращает характеристики кусочно гладкого полинома pp: breaks - вектор разбиения аргумента; coefs - коэффициенты кубических сплайнов;

l = length(breaks) - 1; k = length(coefs)/l.

Функция pp = mkpp(breaks, coefs) формирует кусочно-гладкий полином pp по его характеристикам.

Пример:

Зададим синусоиду всего 10 точками и проведем интерполяцию кубическими сплайнами, используя мелкую сетку.

x = 0:10; y = sin(x); xi = 0:.25:10; yi = spline(x, y, xi); plot(x, y, 'o', xi, yi, ‘g’), grid

Результат интерполяции кубическим сплайном представлен на рисунке 9

Рисунок 9 - Результат интерполяции кубическим сплайном

2.5.3 Одномерная табличная интерполяция interp1

Синтаксис:

yi = interp1(x, y, xi) yi = interp1(x, y, xi, ‘<метод>‘)

Описание:

Функция yi = interp1(x, y, xi) строит интерполирующую кривую для одномерного массива y, заданного на сетке x; выходной массив yi может быть определен на более мелкой сетке xi. Если Y - двумерный массив, то интерполирующая кривая строится для каждого столбца. По умолчанию реализована линейная интерполяция.

Функция yi = interp1(x, y, xi, ‘<метод>‘) позволяет задать метод интерполяции:

‘linear’ линейная

‘cubic’ кубическая

‘spline’ кубические сплайны

Принято, что аргумент x изменяется монотонно; кроме того, для кубической интерполяции предполагается, что сетка по x равномерна.

Пример:

Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.

x = 0:10; y = sin(x); xi = 0:.25:10; yi = interp1(x, y, xi); plot(x, y, 'o', xi, yi, ‘g’), hold on yi = interp1(x, y, xi, ‘spline’ ); plot(x, y, 'ob', xi, yi, ‘m’), grid, hold off

Результат одномерной табличной интерполяции представлен на рисунке 10

Рисунок 10 - Результат одномерной табличной интерполяции

2.5.4 Аппроксимация периодической функции на основе быстрого преобразования Фурье interpft

Синтаксис:

yp = interpft(y, n)

Описание:

Функция yp = interpft(y, n) возвращает одномерный массив чисел, который является периодической функцией, определенной в n точках и аппроксимирующей одномерный массив y. Если length(x) = m, а интервал дискретности dx, то интервал дискретности для y определяется по формуле dy = dx * m/n, причем n всегда превышает m.

Пример:

Рассмотрим аппроксимацию функции y = sin(x), которая задана 11 точками на интервале [0 10].

x = 0:10; y = sin(x); xp = 0:0.25:10; yp = interpft(y, 41); xt = 0:0.01:10; yt = sin(xt); plot(xt, yt, 'r'), hold on, plot(x, y, 'ob', xp, yp)

Результат аппроксимация периодической функции на основе быстрого преобразования Фурье представлен на рисунке 11

Рисунок 11 - Результат аппроксимация функции на основе преобразования Фурье

На графике построена точная функция y = sin(x) с указанием точек съема данных и ее аппроксимация в 41 точке. Как видно из графика, аппроксимация вне интервала [0 1.5] имеет нарастающую погрешность.

3 Решение типовых задач алгебры и анализа в символьной форме

3.1 Обозначения символьных переменных

Под символьным объектом в системе Matlab понимается переменная, предназначенная для символьных преобразований. Объявление такой переменной осуществляется функцией sym либо syms.

Функция syms позволяет объявлять сразу несколько символьных переменных, которые необходимо отделять друг от друга пробелами, например:

» syms x y z;

Функция sym используется при объявлении какой-либо одной переменной символьной, например:

x = sym('x'); y = sym('y'); z = sym('z');

объявление символьных переменных х, y, z.

3.2 Вычисление пределов функций limit

Вычисление пределов от символьных выражений производится с помощью встроенной функции limit. Соответствие между традиционным математическим описанием и символьным системы Matlab приводится в таблице 1.

Таблица 1 – Вычисления пределов

Традиционное математическое действие	Команда MATLAB


	% предел слева
	% предел справа

Примечание: символ бесконечность () вMatlab записывается как inf. Неопределенное значение в Matlab записывается как NaN.

Пример: Вычислить предел выражения :

» syms x

» y1=sin(x)/x;

» limit(y1)

ans =

1 % Предел отношения равен единицы

3.3 Решение алгебраических уравнений и систем solve

Для решения систем алгебраических уравнений и одиночных уравнений служит функция solve:

Синтаксис:

solve(expr1, expr2,..., exprN, var1, var2,..., varN)

Описание:

Функция solve возвращает значения переменных var1, при которых соблюдаются равенства, заданные выражениями expr1. Если в выражениях не используются знаки равенства, то полагается expr1=0.

Результат решения возможен в следующих формах:

- для одного уравнения и одной переменной решение возвращается в виде одномерного или многомерного массива ячеек;

- при одинаковом числе уравнений и переменных решение возвращается в упорядоченном по именам переменных виде;

Функция solve позволяет найти не только вещественные, но и комплексные корни систем алгебраических уравнений и одиночных уравнений.

Пример решить уравнение:

x³- 1=0 (8)

Решение:

>> syms x

>> y=x^3-1;

>> S=solve(y,x)

S =

[ 1]

[ -1/2+1/2*i*3^(1/2)]

[ -1/2-1/2*i*3^(1/2)]

Получили три корня x₁, x₂, x₃, которые хранятся соответственно в элементах S(1), S(2), S(3) массива S.

3.4 Дифференцирование функций diff

Matlab позволяет производить точное дифференцирование в символьном виде, используя следующие функции:

diff(S) дифференцирует символьное выражение S по свободной переменной;
diff(S, ‘v’) дифференцирует символьное выражение S по v;
diff(S, n) и diff(S, ‘v’, n) дифференцирует n раз символьное выражение S;
diff без аргументов дифференцирует предшествующее выражение.

Пример:

Дифференцирование функций одной переменной — diff.

Найти производную функции по переменнойх:

» y6=sin(x+h);

» diff(y6)

ans =

cos(x+h)

3.5 Решение дифференциальных уравнений в символьном виде dsolve

Решатель дифференциальных уравнений может быть использован, если решение существует в аналитическом виде. Практически это означает, что решателем dsolve можно пользоваться только при поиске решения линейного дифференциального уравнения (или системы линейных уравнений).

Решить дифференциальное уравнение с начальным условиемПостроить график решения в интервале [-0.5, 7].

% Создадим следующий сценарий под именем sdif1:

%Решение дифференциального уравнения в символьном виде

x1=dsolve('Dx=-0.5*x','x(0)=10')

ezplot(x1,[-0.5,7]), grid, title('Диф.уравнение')

% Область построения графика решения можно задавать без квадратных скобок

Решить систему однородных дифференциальных уравнений с начальными условиямипостроить график решения в интервале [-0.5, 13].

% Создадим следующий сценарий под именем sdif2:

[x1,x2]=dsolve('Dx1=-.5*x2','Dx2=3*x1','x1(0)=0','x2(0)=1');

ezplot(x1,0,13), grid, hold on, ezplot(x2,[0,13]), title ('Однородная система 2-х уравнений')

3.6 Интегрирование функции одной переменной int

Для вычисления интегралов в символьном виде используется функция int, имеющая следующий синтаксис: int (f), int (f, [u]), int (f, [u , a, b ]),

где f - символьная подынтегральная функция, необязательные переменные:

u - переменная интегрирования,

а - нижний предел интегрирования,

b - верхний предел интегрирования.

Вычисление неопределенного интеграла:

% Вычислить интеграл :

» int(x^2)

ans =

1/3*x^3

Вычисление определенного интеграла:

% Вычислить определенный интеграл :

» y7=int(x^2*sin(x),1,2*pi)

» vpa(y7,5)

ans =

-39.702

4 Модели линейных динамических систем

4.1 Описание линейных динамических систем

Для описания линейных систем могут применяться несколько способов:

дифференциальные уравнения
модели в пространстве состояний
передаточные функции
модели вида «нули-полюса»

Первые два способа называются временныَми, поскольку описывают поведение системы во временной области и отражают внутренние связи между сигналами. Передаточные функции и модели вида «нули-полюса» относятся к частотным способам описания, так как непосредственно связаны с частотными характеристиками системы и отражают только входные и выходные свойства (то есть, описывают динамику не полностью).

Частотные методы позволяют применять для анализа и синтеза алгебраические методы, что часто упрощает расчеты. С другой стороны, для автоматических вычислений более пригодны методы, основанные на моделях в пространстве состояний, поскольку они используют вычислительно устойчивые алгоритмы линейной алгебры.

Исходные уравнения динамики объектов, которые строятся на основе законов физики, имеют вид нелинейных дифференциальных уравнений. Для приближенного анализа и синтеза обычно проводят их линеаризацию в окрестности установившегося режима и получают линейные дифференциальные уравнения.

Линейное уравнение можно записать в операторной форме

или (9)

где – входной сигнал,– сигнал выхода,– оператор дифференцирования,и– операторные полиномы.

Передаточная функция линейной стационарной системы от комплексной переменной определяется как отношение преобразования Лапласа выхода к преобразованию Лапласа входа при нулевых начальных условиях[6]:

(10)

Передаточная функция звена, которое описывается приведенным выше уравнением, равна:

, (11)

Передаточная функция в среде Matlab вводится в виде отношения двух многочленов (полиномов) от при замене комплексной переменной на. Полиномы хранятся как массивы коэффициентов, записанных поубыванию степеней. Например, передаточная функция

(12)

вводится следующим образом:

>> n = [2 4]

n =

2 4

>> d = [1 1.5 1.5 1]

d =

1.0000 1.5000 1.5000 1.0000

>> f = tf ( n, d )

Transfer function:

2 s + 4

-------------------------

s^3 + 1.5 s^2 + 1.5 s + 1

или сразу, без предварительного построения числителя и знаменателя:

>> f = tf ( [2 4], [1 1.5 1.5 1] );

В памяти создается объект класса tf, описывающий передаточную функцию. Точка с запятой в конце команды подавляет вывод на экран.

По передаточной функции можно легко построить модель в форме «нули-полюса»

>> f_zpk = zpk(f)

Zero/pole/gain:

2 (s+2)

-----------------------

(s+1) (s^2 + 0.5s + 1)

Нулями называются корни числителя, полюсами – корни знаменателя. Эта функция имеет один нуль в точке и три полюса в точкахи. Паре комплексных полюсов соответствует квадратный трехчлен.

Модель в пространстве состояний связана с записью дифференциальных уравнений в стандартной форме Коши (в виде системы уравнений первого порядка) [6]:

(13)

Здесь – вектор переменных состояния размера,– вектор входных сигналов (вектор управления) размераи– вектор выходных сигналов размера. Кроме того,и– постоянные матрицы. Согласно правилам матричных вычислений, матрицадолжна быть квадратной размера, матрицаимеет размер, матрица–и матрица–. Для систем с одним входом и одним выходом матрица– скалярная величина.

Для преобразования передаточной функции в модель в пространстве состояний используется команда

>> f_ss = ss ( f )

a =

x1 x2 x3

x1 -1.5 -0.1875 -0.03125

x2 8 0 0

x3 0 4 0

b =

x1 0.5

x2 0

x3 0

c =

x1 x2 x3

y1 0 0.5 0.25

d =

y1 0

Это означает, что матрицы модели имеют вид

, ,,.

Модель в пространстве состояний можно построить не для всех передаточных функций, а только для правильных, у которых степень числителя не выше, чем степень знаменателя. Например, передаточная функция

(14)

– неправильная, она не может быть преобразована в модель в пространстве состояний.

Используют также понятие строго правильной функции, у которой степень числителя меньше, чем степень знаменателя. Если построить модель в пространстве состояний для такой функции, матрица будет равна нулю, то есть, прямая передача с входа на выход отсутствует (при скачкообразном изменении входа сигнал на выходе будет непрерывным).

Коэффициент усиления в установившемся режиме

Одна из важнейших характеристик линейной системы – коэффициент усиления в установившемся режиме или статический коэффициент усилении (static gain, DC-gain). Его можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице. Размерность этой величины равна отношению размерностей сигналов выхода и выхода.

Рассмотрим дифференциальное уравнение

. (15)

Полагая все производные (в установившемся режиме) равными нулю, получаем

. (16)

Статический коэффициент усиления равен .

Если задана передаточная функции, для вычисления надо подставить в нее, поскольку переменнаясоответствует оператору дифференцирования. Рассмотренному выше уравнению можно сопоставить передаточную функцию:

. (17)

Тогда:

. (18)

Если система содержит интегрирующее звено (передаточная функция имеет полюс в точке ), этот предел равен бесконечности, то есть, при постоянном сигнале выход бесконечно увеличивается или уменьшается, не достигая установившегося режима.

Тот же результат можно получить с помощью эквивалентной модели в пространстве состояний. С помощью среды Matlab находим

Полагая , получаем модель, определяющую установившийся режим:

, (19)

откуда следует

. (20)

Для нашей системы, как и раньше, получаем . Заметьте, что для того, чтобы статический коэффициент усиления был конечен, требуется обратимость матрицы, то есть, отсутствие интегрирующих звеньев.

Чтобы найти статический коэффициент усиления модели f в Matlab, используется команда

>> k = dcgain ( f )

Импульсная характеристика

Импульсной характеристикой (весовой функцией) называется реакция системы на единичный бесконечный импульс (дельта-функцию или функцию Дирака) при нулевых начальных условиях. Дельта-функцияопределяется равенствами [6]:

, . (21)

Это обобщенная функция – математический объект, представляющий собой идеальный сигнал, никакое реальное устройство не способно его воспроизвести. Дельта-функцию можно рассматривать как предел прямоугольного импульса единичной площади с центром в точке при стремлении ширины импульса к нулю. (Рисунок 12)

Рисунок 12 - Дельта-функция

Второе название – весовая функция – связано с тем, что для произвольного входного сигнала выход системывычисляется как свертка [6]:

. (22)

Здесь функция как бы «взвешивает» входной сигнал в подынтегральном выражении.

Импульсная характеристика отражает лишь вход- выходные соотношения при нулевых начальных условиях, то есть, не может полностью описывать динамику системы.

Переходная характеристика

Переходной характеристикой (переходной функцией) называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок) (Рисунок 13) [6]:

. (23)

Импульсная и переходная функции связаны выражениями:

, . (24)

Для систем без интеграторов переходная характеристика стремится к постоянному значению. Переходная характеристика системы с дифференцирующим звеном (числитель передаточной функции имеет нуль в точке ) стремится к нулю.

Рисунок 13 – Переходная характеристика

По определению предельное значение переходной функции приесть статический коэффициент усиления:

. (25)

Эта величина имеет смысл только для устойчивых систем, поскольку при неустойчивости переходный процесс не сходится к конечному значению.

По переходной характеристике можно найти важнейшие показатели качества системы – перерегулирование (overshoot) и время переходного процесса (settling time). (Рисунок 14)

Перерегулирование определяется как:

, (26)

где – максимальное значение функции, а– установившееся значение выхода.

Время переходного процесса – это время, после которого сигнал выхода отличается от установившегося значения не более, чем на заданную малую величину (в среде Matlab по умолчанию используется точность 2%).

Рисунок 14 – Определение времени переходного процесса и перерегулирования

Частотная характеристика

При подаче на вход линейной системы гармонического (синусоидального) сигнала с частотой(она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы, где– амплитуда и– сдвиг фазы.

Частотная характеристика определяется как реакция системы на комплексный экспоненциальный сигнал . Для ее построения надо использовать подстановкув передаточной функции. Выражениеназываетсячастотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).

Зависимость модуля величины от частоты называетсяамплитудной частотной характеристикой (АЧХ) (Рисунок 15), а зависимость аргумента комплексного числа (фазы) от частоты –фазовой частотной характеристикой (ФЧХ) [6]:

. (27)

АЧХ показывает, насколько усиливается амплитуда сигналов разных частот после прохождения через систему, а ФЧХ характеризует сдвиг фазы сигнала.

Рисунок 15– Амплитудно – частотная характеристика

Реальные объекты имеют строго правильную передаточную функцию, поэтому их АЧХ убывает с ростом частоты и асимптотически стремится к нулю. Говорят, что такой объект обладает свойством фильтра – фильтрует (не пропускает) высокочастотные сигналы (помехи, шумы измерений). Это свойство служит основой для использования метода гармонического баланса.

Частота, после которой значение АЧХ уменьшается ниже 0 дБ (коэффициент усиления меньше 1, сигнал ослабляется), называется частотой среза системы .

Частота, после которой значение АЧХ падает ниже -3 дБ (коэффициент усиления меньше, чем 0.708), называется полосой пропускания системы . Для ее вычисления используют команду:

>> b = bandwidth ( f )

Максимум АЧХ соответствует частоте, на которой усиление наибольшее. Значение АЧХ при равно усилению при постоянном сигнале, то есть, статическому коэффициенту усиления. Это следует и из равенства:

. (28)

Для систем с интегрирующими звеньями частотная характеристика стремится к бесконечности при . Это значит, что их выход бесконечно увеличивается или уменьшается при постоянном входном сигнале.

Чтобы построить частотные характеристики в Matlab, надо сначала создать массив частот в нужном диапазоне. Для этого можно использовать функции linspace (равномерное распределение точек по линейной шкале) и logspace (равномерное распределение точек по логарифмической шкале). Команда:

>> w = linspace (0, 10, 100);

строит массив из 100 точек с равномерным шагом в интервале от 0 до 10, а команда

>> w = logspace (-1, 2, 100);

– массив из 100 точек с равномерным шагом по логарифмической шкале в интервале от до.

Частотная характеристика на сетке w для линейной модели f (заданной как передаточная функция, модель в пространстве состояний или в форме «нули-полюса») вычисляется с помощью функции freqresp:

>> r = freqresp(f, w);

Функция freqresp возвращает трехмерный массив. Это связано с тем, что она применима и для многомерных моделей (с несколькими входами и выходами), передаточная функция которых представляет собой матрицу. Первые два индекса обозначают строку и столбец в этой матрице, а третий – номер точки частотной характеристики. Для системы с одним входом и одним выходом удобно преобразовать трехмерный массив в одномерный командой

>> r = r(:);

Для вывода графика АЧХ на экран можно использовать команды Matlab

>> plot ( w, abs(r) );

>> semilogx ( w, abs(r) );

>> loglog ( w, abs(r) );

В первом случае масштаб обеих осей координат – линейный, во втором случае используется логарифмический масштаб по оси абсцисс (частот), в последнем – логарифмический масштаб по обеим осям. Для вычисления фазы (в градусах) используется команда:

>> phi = angle(r)*180/pi;

после чего можно строить ФЧХ, например:

>> semilogx ( w, phi );

Полюса и нули

Многие динамические свойства системы (например, быстродействие, перерегулирование) определяются полюсами передаточной функции (или, что то же самое, собственными числами матрицы модели в пространстве состояний).

Передаточную функцию можно записать как произведение передаточных функций элементарных звеньев первого и второго порядков. Таким образом, множество полюсов передаточной функции устойчивой системы составляют полюса передаточных функций двух типов простейших звеньев: апериодических и колебательных.

Апериодическое звено с передаточной функцией вида имеет единственную характеристику – постоянную времени. Начиная примерно с частоты, АЧХ такого звена начинает убывать, приближаясь к нулю.

Колебательное звено имеет передаточную функцию , где– постоянная времени и. Частотаназываетсясобственной частотой (natural frequency), а параметр –параметром затухания или коэффициентом демпфирования (damping factor). При уменьшении импульсная и переходная функции приобретают ярко выраженный колебательный характер, а на АЧХ появляется «горб» в районе частоты. В предельном случае приколебания становятся незатухающими, а звено называетсяконсервативным. С другой стороны при корни знаменателя становятся вещественными, и звено превращается в апериодическое звено второго порядка.

Для нахождения полюсов передаточной функции f можно использовать функцию:

>> p = pole ( f )

Вызов функции:

>> [w0,zeta,p] = damp ( f )

позволяет найти не только полюса p, но также соответствующие им собственные частоты w0 и коэффициенты демпфирования zeta в виде массивов.

Нули передаточной функции f вычисляются как

>> z = zero ( f );

Устойчивость системы не зависит от расположения нулей, но они существенно влияют на переходные процессы. Команда:

>> pzmap ( f );

строит карту расположения нулей (они обозначаются кружками) и полюсов (крестики) системы на комплексной плоскости.

Передаточные функции типовых звеньев приведены в таблице 2 [6]:

На практике часто требуется найти эквивалентную передаточную функцию, которую можно получить путем сворачивания звеньев с использованием следующих правил.

При последовательном соединении звеньев выходная величина каждого предыдущего звена является выходной величиной для последующего звена (Рисунок 16, а).

Передаточная функция последовательно соединённых звеньев равна произведению передаточных функций отдельных звеньев (Рисунок 16а) [6]:

(29)

Таблица 2- Передаточные функции типовых звеньев

№ п.п.	Название звена	ПФ звена
1	Интегрирующие (И)
2	Дифференцирующие (Д)
3	Усилительное (У) (безынерционное)
4	Апериодическое 1-го порядка (А) (инерционное)
5	Апериодическое 2-го порядка (А2) (все корни вещественные)	,
6	Колебательное (К)	, ζ < 1.
7	Консервативное (КОН)
8	Интегрирующие с запаздыванием (реальное интегрирующие) (ИЗ)
9	Дифференцирующее с запаздыванием (реальное дифференцирующее) (ДЗ)

Параллельное соединение звеньев – соединение, при котором входная величина является общей для всех звеньев (Рисунок 1, б). Передаточная функция параллельно соединённых звеньев равна сумме передаточных функций отдельных звеньев [6]:

(30)

Встречно – параллельное соединение звеньев, в состав которого входит положительная или отрицательная обратная связь (Рисунок 16, в). Передаточную функцию для такого соединения звеньев определяют по формуле [6]:

(31)

а-последовательное; б-параллельное; в- встречно - параллельное

Рисунок 16- Соединение звеньев

Для получения эквивалентной передаточной функциив среде Matlab нужно ввести требуемые функции с помощью команды tf и произвести необходимые преобразования по формулам 29 – 31.

Основная часть команд вводится в командном окне среды Matlab. Команды, которые надо применять в других окнах, обозначены иконками соответствующих программ. Пример выполнения задания рассмотрим на примере передаточной функции:

(32)

5 Выполнение анализа динамической системы в среде Matlab

Этапы выполнения анализа динамической системы приведены в таблице 3

Таблица 3 -Этапы выполнения анализа динамической системы

Этап выполнения задания	Команды Matlab
Очистите рабочее пространство Matlab(память).	clear all
Очистите окно Matlab.	clc
Посмотрите краткую справку по команде tf.	help tf
Определите адрес файла, который выполняет эту команду.	which('tf')
Введите передаточную функцию как объектtf.	n = [n2 n1 n0] d = [1 d2 d1 d0] f = tf ( n, d )
Проверьте, как извлечь из этого объекта числитель и знаменатель передаточной функции.	[n1,d1] = tfdata ( f, 'v' )
Найдите нули и полюса передаточной функции.	z = zero ( f ) p = pole ( f )
Найдите коэффициент усиления звена в установившемся режиме.	k = dcgain ( f )
Определите полосу пропускания системы (наименьшую частоту, на которой АЧХ становится меньше, чем дБ).	b = bandwidth ( f )
Постройте модель системы в пространстве состояния.	f_ss = ss ( f )
Сделайте так, чтобы коэффициент прямой передачи звена был равен 1.	f_ss.d = 1
Найдите новый коэффициент усиления звена в установившемся режиме.	k1 = dcgain ( f_ss )
Как связаны коэффициенты и? Почему?
Постройте модель исходной системы в форме «нули-полюса».	f_zp = zpk ( f )
Проверьте, какие переменные есть в рабочем пространстве.	who или whos (в чем разница?)
Постройте на графике расположение нулей и полюсов системы.	pzmap ( f )
Определите коэффициенты демпфирования и собственные частоты для всех элементарных звеньев (первого и второго порядка).	[wc,ksi,p] = damp ( f )
Запустите модуль LTIViewer.	ltiview
Загрузите модель f.	File – Import
Постройте импульсную характеристику (весовую функцию) этой системы.	ПКМ – Plot Types - Impulse
Загрузите модель f_ss.	File – Import
Проверьте, построена ли импульсная характеристика второй системы?	ПКМ – Systems
Отключите систему f. Почему одинаковы построенные импульсные характеристики разных систем?	ПКМ – Systems
Подключите обе системы.	ПКМ – Systems
Постройте переходные характеристики систем.	ПКМ – Plot Types – Step
Сделайте, чтобы на графике для каждой функции были отмечены: максимум время переходного процесса время нарастания (от 10% до 90% установившегося значения) установившееся значение	ПКМ – Characteristics: Peak Response Settling Time Rise Time Steady State
Щелкая мышью по меткам-кружкам, выведите на экран рамки с численными значениями этих параметров и расположите их так, чтобы все числа были видны.
Экспортируйте построенный график в отдельное окно.	File – Print to Figure
Скопируйте график в буфер обмена в формате векторного метафайла.	print -dmeta
Вставьте график из буфера обмена в отчет (Microsoft Word).	ПКМ - Вставить
Закройте окно LTIViewer.
Создайте массив частот для построения частотной характеристики (100 точек в интервале от дос равномерным распределением на логарифмической шкале).	w = logspace(-1, 2, 100);
Рассчитайте частотную характеристику исходной системы …	r = freqresp ( f, w ); r = r(:);
… и постройте ее на осях с логарифмическим масштабом по оси абсцисс.	semilogx ( w, abs(r) )
Скопируйте график в буфер обмена в формате векторного метафайла.	print -dmeta
Вставьте график из буфера обмена в отчет (Microsoft Word). Объясните, где на графике можно найти коэффициент усиления в статическом режиме и как определить полосу пропускания системы.	ПКМ – Вставить
Закройте все лишние окна, кроме командного окна Matlab.
Постройте сигнал, имитирующий прямоугольные импульсы единичной амплитуды с периодом 4 секунды (всего 5 импульсов).	[u,t] = gensig('square',4);
Выполните моделирование и постройте на графике сигнал выхода системы fпри данном входе.	lsim (f, u, t)
Скопируйте график в буфер обмена в формате векторного метафайла.	print -dmeta
Вставьте график из буфера обмена в отчет (Microsoft Word).	ПКМ – Вставить

6 Создание моделей в среде Simulink

Пакет Simulink предназначен для моделирования систем. Вся модель строится из блоков, имеющих входы и выходы. Существует библиотека стандартных блоков, кроме того, можно создавать свои собственные блоки любой сложности.

Существует две группы специальных устройств – источники сигналов (Sources) и устройства вывода (Sinks).

Блоки имеют названия. Для того, чтобы изменить название, надо щелкнуть по нему ЛКМ и отредактировать текст.

Каждый блок имеет свои настраиваемые свойства. Для их изменения надо дважды щелкнуть на блоке и изменить нужные значения в диалоговом окне.

Для того, чтобы повернуть блок на 90 градусов, надо выделить его и нажать клавиши Ctrl+R. Комбинация Ctrl+I позволяет выполнить зеркальное отражение входов и выходов.

Верхнее меню Format предназначено для изменения оформления выделенного блока. Также для этой цели можно использовать контекстное меню ПКМ – Format. Для выделенного блока можно изменить цвет текста и линий (Foreground color), цвет фона (Background color), вывести тень (Show drop shadow), переместить название на другую сторону (Flip name).

Для выделения одного блока или соединительной линии надо щелкнуть ЛКМ по нужному элементу. Для того, чтобы выделить несколько блоков, надо «обвести» их при нажатой ЛКМ. Клавиша Delete удаляют выделенную часть. Чтобы скопировать блок (или выделенную часть), надо перетащить его при нажатой правой кнопке мыши (ПКМ).

Блоки соединяются линиями связи, по которым распространяются сигналы. Для того, чтобы соединить блоки, надо щелкнуть ЛКМ по источнику сигнала и затем, при нажатой клавише Ctrl, по блоку-приемнику. Можно также протянуть мышкой линию связи между нужными выходом и входом.

Чтобы подать один сигнал на два блока (сделать «развилку»), надо сначала создать одну линию обычным способом. Чтобы провести вторую линию, следует нажать правую кнопку мыши на линии в точке развилки и протащить линию ко второму блоку. Модель можно скопировать в буфер обмена в виде растрового рисунка. Для этого в окне модели надо выбрать в верхнем меню пункт Edit – Copy model to clipboard. Предварительно лучше уменьшить размеры окна до минимальных, чтобы не было белых полей.

Для того, чтобы запустить моделирование, надо щелкнуть ЛКМ по кнопке на панели инструментов. Эта же кнопка позволяет остановить моделирование при необходимости. Параметры моделирования (метод интегрирования, обработка ошибок) устанавливаются с помощью окнаSimulation – Parameters. Самые важные параметры – это время моделирования (Stop time) и метод численного интегрирования уравнений (Solver options). Основные источники сигналов (Sources) приведены в таблице 4.

Таблица 4 - Основные источники сигналов

	Constant– сигнал постоянной величины.
	Step– ступенчатый сигнал, меняется время скачка (Step Time), начальное (Initial Value) и конечное значение (Final Value).
	Ramp – линейно возрастающий сигнал с заданным наклоном (Slope). Можно задать также время начала изменения сигнала (Start Time) и начальное значение (Initial Value).
	Pulse Generator – генератор прямоугольных импульсов, задаются амплитуда (Amplitude), период (Period), ширина (Pulse Width, в процентах от периода), фаза (Phase Delay).
	Repeating Sequence – последовательность импульсов, их форма задается в виде пар чисел (время; величина сигнала)
	Sine Wave – синусоидальный сигнал, задается амплитуда (Amplitude), частота (Frequency), фаза (Phase) и среднее значение (Bias).
	Signal Builder– построитель сигналов, позволяющий задавать форму сигнала, перетаскивая мышью опорные точки.
	Random Number– случайные числа с нормальным (гауссовым) распределением. Можно задать среднее значение (Mean Value), дисперсию (Variance), период изменения сигнала (Sample Time).
	Uniform Random Number – случайные числа с равномерным распределением в заданном интервале отMinimum доMaximum.
	Band Limited White Noise – случайный сигнал, ограниченный по полосе белый шум (имеющий равномерный спектр до некоторой частоты). Блок используется как источник белого шума для моделей непрерывных систем. Задается интенсивность (Noise Power) и интервал дискретизации (Sample Time), в течение которого удерживается постоянное значение сигнала. Чем меньше интервал, тем точнее моделирование, однако больше вычислительные затраты.

Основные устройства вывода (Sinks) приведены в таблице 5

Таблица 5 – Основные устройства вывода

	Display – цифровой дисплей, показывает изменение входного сигнала в цифровом виде.
	Scope – осциллограф, показывает изменение сигнала в виде графика, позволяет передавать данные в рабочую областьMatlabдля последующей обработки и оформления.

Линейные системы (Continuous) приведены в таблице 6

Таблица 6 – Линейные системы

	Transfer Fcn – передаточная функция, в параметрах задаются числитель (Numerator) и знаменатель (Denominator) в виде полиномов.
	State Space – модель в пространстве состояний, в параметрах задается четверка матриц, определяющих модель, и начальные условия для вектора состояния (Initial conditions).
	Zero-Pole – модель в форме «нули-полюса», в параметрах задаются массивы нулей (Zeros), полюсов (Poles), а также коэффициент усиления (Gain).
	Integrator – интегратор с возможностью установки начальных условий (Initial condition), а также пределов насыщения (Lower saturation limitиUpper saturation limit). Когда сигнал выхода выходит за границы, определяемые этими пределами, интегрирование прекращается.
	Derivative - Блок вычисления производной, используется как дифференцирующее звено. Значение входного сигнала блока до начала расчета считается равным нулю. Начальное значение выходного сигнала также полагается равным нулю.

Часто используемые блоки приведены в таблице 7

Таблица 7 – Часто используемые блоки

	Gain – усилитель, задается коэффициент усиления (Gain).
	Sum – сумматор, используется для сложения и вычитания входов. ПараметрList of signsзадает количество входов, их знаки («+» для сложения и «–» для вычитания). Промежутки между входами (обозначаются знаком\|).
	Trigonometric Function – тригонометрическая функция.
	Manual Switch – ручной переключатель, позволяет двойным щелчком переключать выход на один из двух входных сигналов.
	Mux – мультиплексор, объединяет несколько сигналов в один «жгут» (векторный сигнал), в параметрах задается число входов (Number of Inputs).
	Demux – демультиплексор, позволяет «разбить» векторный сигнал на несколько скалярных, в параметрах задается число выходов (Number of Outputs).

Блок осциллографа Scope

В окне блока Scope (Рисунок 17) изображается график изменения входного сигнала. Если вход соединен с выходом мультиплексора, сразу строится несколько графиков (по размерности входного «жгута»).

Рисунок 17 – Окно осциллографа Scope

По умолчанию на оси ординат используется диапазон от -5 до 5. Если этот вариант не подходит, выбрать масштаб автоматически (так, чтобы весь график был виден) можно с помощью кнопки . Соседняя кнопка сохраняет эти настройки для следующих запусков.

Кнопка открывает окно настроек, причем наиболее важные данные содержатся на вкладкеData history. Если не сбросить флажок Limit data points, в памяти будет сохраняться только заданное число точек графика, то есть, при большом времени моделирования начало графика будет потеряно.

Отметив на этой же странице флажок Save data to workspace можно сразу передать результаты моделирования в рабочую область Matlab для того, чтобы их можно было дальше обрабатывать, выводить на графики и сохранять в файле. Поле Variable name задает имя переменной в рабочей области, в которой сохраняются данные. В простейшем случае выбирается формат Array (в списке Format). Это означает, что данные будут сохраняться в массиве из нескольких столбцов (первый столбец – время, второй – первый сигнал, третий – второй сигнал и т.д., по порядку входов мультиплексора).

Оформление графиков

Для создания нового окна для рисунка в Matlab используется команда

>> figure(1);

Вместо единицы можно ставить любой номер рисунка. Если рисунок с таким номером уже есть, он становится активным и выводится на первый план. Если такого рисунка нет, он создается и становится активным. Matlab

В Matlab есть возможность строить несколько графиков на одном рисунке. Иначе говоря, рисунок можно разбить на «клетки», в каждой из которых строится отдельный график. Для этого надо сделать активным нужный рисунок и применить команду:

>> subplot(2, 1, 1);

Первое число в команде subplot показывает количество «строк» в такой матрице, второе – количество столбцов, третье – какой по счету график сделать активным (считая по строкам, справа налево и сверху вниз). Все дальнейшие команды (plot, title, xlabel, ylabel, legend и др.) относятся к этому «подграфику».

В командах можно передавать в качестве аргументов не целые массивы, а их части. Например, по команде

>> plot(x(1:20), y(11:30));

строится график, на котором по оси абсцисс откладываются значения элементов массива x с номерами от 1 до 20, а по оси ординат – соответствующие им значения из массива y с номерами от 11 до 30.

Двоеточие означает «все строки» или «все столбцы». Например, по команде

>> plot(x(:,1), x(:,2));

строится зависимость между первым и вторым столбцами массива x (здесь двоеточие вместо первого индекса обозначает «все строки»).

С помощью команды plot (а также и других подобных – semilogx, semilogy, loglog) можно строить несколько линий на одном графике. Для этого среди аргументов перечисляются пары массивов:

>> plot(x, y, v, z);

Первая линия будет показывать зависимость y от x, а вторая – зависимость z от v. массивы в каждой паре должны быть одинаковой длины. При желании можно указать цвета для каждой линии, Например,

>> plot(x, y, 'b', v, z, 'g');

Первая линия (зависимость y от x) будет синей, вторая (зависимость z от v) – зеленой. Можно использовать следующие цвета: b - синий (blue); g - зеленый (green); r - красный (red); c - голубой (cyan); m - фиолетовый (magenta); y - желтый (yellow); k - черный (black).

По умолчанию первая линия – синяя, вторая – зеленая и т.д. в порядке перечисления цветов в списке. Дополнительно можно указать тип линии

- сплошная

: точечная

-. штрих-пунктирная

-- штриховая

Например,

>> plot(x, y, 'b:', v, z,'g--');

Первая линия – точечная синего цвета, вторая – штриховая зеленого цвета. По умолчанию все линии сплошные.

Для оформления графика также используются команды

title заголовок графика

xlabel название оси абсцисс

ylabel название оси ординат

У всех этих команд обязателен один аргумент – текст в апострофах.

Команда legend служит для вывода легенды графика. Легенда нужна, если на графике есть несколько линий и надо показать, что обозначает каждая из них. Параметрами команды legend являются символьные строки, их должно быть столько, сколько построено линий. Simulink

7 Моделирование линейной системы в пакете Simulink

7.1 Описание линейной системы

Рассмотрим линейную систему управления, структурная схема, которой представлена на рисунке 18.

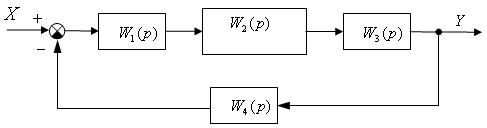
Рисунок 18 - Структурная схема системы управления

Передаточные функции имеют следующий вид:

; (33)

; (34)

; (35)

. (36)

Выполнение анализа линейной динамической системы в среде Simulink

Пример выполнения исследования линейной системы в среде Simulink представлен в таблице 8

Таблица 8 - Пример выполнения исследования линейной система в среде Simulink

Этап выполнения задания	Команды Matlab
1 Для запуска пакета Simulink щелкните по кнопкев командном окнеMatlab или введите команду simulink в командной строке.	simulink
2 Создайте новую модель с помощью верхнего меню открывшегося окна Simulink Library Browser.	File – New – Model
Перетащите блок Transfer Fcn(передаточная функция) из окнаSimulink Library Browser(группаContinuous) в окно модели и введите числитель и знаменатель передаточной функции модели.	Двойной щелчок на блоке Numerator [K] Denominator [ 1 0]
Дайте блоку название W3.	ЛКМ на имени блока
Аналогично добавьте еще три блока типа Transfer Fcn, назовите ихW2,W1иW4,введите нужные параметры. Заметьте, что передаточная функция привода должна бытьс учетом внутренней обратной связи.
Сохраните модель в своей папке под именем lab3.mdl. или под другим именем	File – Save
Выделите блок W4 и разверните его в другую сторону.	Нажать Ctrl+I или дважды нажать Ctrl+R.
Сделайте, чтобы названия блоков W1, W2 и W3 были над блоками.	ПКМ на блоке, Format - Flip name
Выберите цвет блоков на свой вкус.	ПКМ на блоке, Format – Background color
Перетащите в окно модели блок Sumиз группыMath Operationsи установите его слева отW1.	ЛКМ
Сделайте так, чтобы второй вход учитывался в сумме со знаком минус (отрицательная обратная связь).	Двойной щелчок на блоке, ввести \|+- в поле List of signs
Перетащите в окно модели блок Stepиз группыSourcesи установите его слева от сумматора. Дайте ему имяВХОД.
Установите время подачи сигнала 0 и величину сигнала 10.	Двойной щелчок на блоке, 0 в поле Step time 10 в поле Final value
Соедините все блоки нужным способом.	ЛКМ на источнике, удерживать Ctrl и ЛКМ на приемнике, или протащить ЛКМ от выхода одного блока к входу другого
Перетащите в окно модели два блока Scope(осциллограф) из группыSinksи установите их в правой части. Назовите ихСигн1иСигн2.
Сделайте, чтобы на первый блок Scopeпоступал сигналcблокаW2, а на второй – сигналcблокаW3. Сохраните модель.	Нажать ПКМ на линии в точке отбора сигнала, затем, не отпуская ПКМ, тащить линию к входу блока.
Уменьшите окно до минимального размера, при котором видны все элементы, и скопируйте модель в буфер обмена. Затем вставьте ее из буфера обмена в отчет.	Edit – Copy model to clipboard
Установите время моделирования 100 секунд.	Simulation – Simulation parameters 100 в поле Stop time
Выполните моделирование.	ЛКМ по кнопке
Посмотрите результаты моделирования, открыв окна для блоков Сигн1 иСигн2.	Двойной щелчок по блоку
Настройте масштаб по осям в окнах обоих блоков,	ЛКМ по кнопке – установить оптимальный масштаб
Сохраните настройки,	ЛКМ по кнопке
Сделайте так, чтобы результаты моделирования передавались с обоих блоков Scopeв рабочую областьMatlab в виде матриц, в которых первый столбец – время, а второй – сигнал (Сигн1 или Сигн2).	ЛКМ по кнопке вкладка Data history Variable name: Y1 (Сигн1) или Y2 (Сигн2) Format: Array
Выполните моделирование еще раз.	ЛКМ по кнопке
Перейдите в командное окно Matlabи создайте новое окно для графика. В одном окне будут построены две кривых на разных осях.	figure(1);
Разбейте окно на 2 части по вертикали и сделайте активным первый график. Первое число в команде subplot означает количество ячеек с графиками по вертикали, второе – по горизонтали, третье – номер ячейки, которую надо сделать активной.	subplot(2, 1, 1);
Постройте график изменения Y1. В командеplotсначала указывают массив абсцисс, затем – массив ординат. Двоеточие означает, что используются все строки.	plot(Y1(:,1),Y1(:,2));
Введите заголовок графика.	title('y1');
Введите названия осей координат. Внутри апострофов для ввода греческих букв разрешается использовать команды LaTeX,	xlabel('Время, сек'); ylabel('\Y1, V');
Аналогично постройте во второй ячейке график изменения угла поворота руля, используя данные из массива Y1, полученного в результате моделирования.	subplot(2, 1, 2); plot(Y2(:,1),Y2(:,2)); title('Выходной сигнал'); xlabel('Время, сек'); ylabel('Y2, V');
Скопируйте построенный график в отчет.	print -dmeta

8 Порядок выполнения домашних работ

Номер варианта задания определяется в соответствие с порядковым номером студента в ведомости, варианты заданий приведены в таблицах 5-10, Таблицы 4 и 5 являются общими для выполнения заданий 1 и 2. В соответствии с учебным планом выполняется следующие 3 задания:

- решение типовых задач алгебры, анализа и в Matlab;

- решение типовых задач алгебры и анализа в символьной форме

- исследование линейной динамической системы в Matlab и Simulink.

Все задания выполняются в соответствии с примерами, приведенными в методических рекомендациях. Выполненные задания, представляются в электронном и бумажном виде. Пример обложки для оформления задания приведен в приложении А.

8.1 Порядок выполнения домашней работы № 1

1 решить систему линейных алгебраических уравнений (п. 2.1);

2 решить дифференциальное уравнение (п. 2.2);

3 вычислить определенный интеграл (п. 2.3 и 2.4) методами трапеций и квадратур;

4 выполнить кубическую интерполяция функции одной переменной (п. 2.5.1);

5 выполнить интерполяцию функции кубическим сплайном (п. 2.5.2);

6 выполнить одномерную табличную интерполяция (п. 2.5.3);

7 выполнить аппроксимацию табличных данных на основе быстрого преобразования Фурье (п. 2.5.4).

8.2 Порядок выполнения домашней работы № 2

1 вычислить символьными методами предел функции (п. 3.2);

2 решить символьными методами алгебраическое уравнение (п. 3.3);

3 произвести дифференцирование функции в символьном виде (п.3.4), кроме того к указанной функции применить 3-х кратное дифференцирование.

4 решить в символьном виде дифференциальное уравнение (п. 3.5);

5 вычислить в символьном виде неопределенный и определенный интегралы (п. 2.3 и 2.4).

8.3 Порядок выполнения домашней работы № 3

1 по данным таблицы 16 получить эквивалентную передаточную функцию средствами Matlab (п. 4.1);

2 произвести исследование линейной системы средствами Matlab (п. 5);

3 в соответствии данным таблицы 16 собрать структурную схему системы в Simulink (п. 6 и 7.1);

4 произвести исследование линейной системы средствами Simulink (п. 7.2);

9 Варианты заданий для выполнения домашних работ

Варианты заданий для решения систем линейных алгебраических уравнений вида А*Х = В и дифференциальных уравнений вида , вычисления интегралов и интерполяции и аппроксимации данных представлены в таблицах 9 -12, соответственно.Вариант в таблице 12 значений функции f(x), начиная с узла, равного номеру вашего варианта и заканчивается на номере перед следующим вариантом (например вариант № 13 начинается со значений Х = 13 и заканчивается значением Х=13.9).

Таблица 9 – Варианты заданий для решения систем алгебраических уравнений

№ вар	A				B	№ вар	A				B
1	1	0.47	-0.11	0.55	1.33	2	0.63	1	0.11	0.34	2.08
	0.42	1	0.35	0.17	1.29		0.17	1.18	-0.45	0.11	0.17
	-0.25	0.67	1	0.36	2.11		0.31	-0.15	1.17	-2.35	1.28
	0.54	-0.32	-0.74	1	0.10		0.58	0.21	-3.45	-1.18	0.05
3	0.77	0.04	-0.21	0.18	1.24	4	0.79	-0.12	0.34	0.16	-0.64
	-0.45	1.23	-0.06	0	-0.88		-0.34	1.18	-0.17	0.18	1.42
	-0.26	-0.34	1.11	0	0.62		-0.16	-0.34	0.85	0.31	-0.42
	-0.05	0.26	-0.34	1.12	-1.17		-0.12	0.26	0.08	0.75	0.83
5	-0.68	-0.18	0.02	0.21	-1.83	6	-0.58	-0.32	0.03	0	-0.44
	0.16	-0.88	-0.14	0.27	0.65		0.11	-1.26	-0.36	0	-1.42
	0.37	0.27	-1.02	-0.24	-2.23		0.12	0.08	-1.14	-0.24	0.83
	0.12	0.21	-0.18	-0.75	1.13		0.15	-0.35	-0.18	0	1.42
7	-0.83	0.31	-0.18	0.22	1.71	8	-0.87	0.27	-0.22	-0.18	-1.21
	-0.21	-0.67	0	0.22	-0.62		-0.21	-1.	-0.45	0.18	0.33
	0.32	-0.18	-0.95	-0.19	0.89		0.12	0.13	-0.33	0.18	0.48
	0.12	0.28	-0.14	-1	-0.94		0.33	-0.41	0	-1	1.21
9	-0.81	-0.07	0.38	-0.21	0.81	10	-1	0.22	-0.11	0.31	-2.7
	-0.22	-0.92	0.11	0.33	0.64		0.38	-1	-0.12	0.22	1.5
	0.51	-0.07	-0.81	-0.11	1.71		0.11	0.23	1	-0.51	1.2
	0.33	-0.41	0	-1	1.21		0.17	-0.21	0.31	-1	0.17
11	-0.93	-0.08	0.11	-1.18	0.51	12	-0.95	-0.06	-0.12	0.14	2.17
	0.18	-0.48	0	0.21	-1.17		0.04	-1.12	0.08	0.11	1.4
	0.13	0.31	-1	-0.21	1.02		0.11	0.12	0	1.03	0.8
	0.08	0	-0.33	-0.72	0.28		0.34	0.08	-1.06	0.14	2.1
13	0	-0.19	0.27	-0.88	1.2	14	-0.88	-0.23	0.25	-0.16	1.24
	-0.33	-1	-0.07	0.21	0.92		0.33	0.03	-0.84	-0.32	-1.15
	0.11	0	1.03	-0.42	0.92		0.14	-0.66	-0.18	0.24	0.89
	-0.92	-0.03	0	-0.04	1.2		0.12	-0.05	0	-0.85	0.57
15	0.12	-1	0.32	-0.18	0.72	16	-0.86	0.23	0.18	0.17	1.42
	0.08	-0.12	-0.77	0.32	0.58		0.12	-1.14	0.08	0.09	0.83
	0.25	0.22	0.14	-1	-1.56		0.16	0.24	-1	-0.35	-1.21
	-0.77	-0.14	0.06	-0.12	-1.21		0.23	-0.08	0.05	-0.75	-0.65
17	76	21	6	-34	-142	18	-83	27	-13	-11	142
	12	-114	8	9	83		5	-68	13	24	26
	16	24	-100	-35	-121		9	54	127	36	23
	23	8	5	-75	85		13	27	34	156	49
19	1	2	5	9	1.11	20	-1	0.28	-0.17	0.06	-21
	2	1	9	4	1.16		0.52	-1	0.12	0.17	117
	3	9	1	4	1.24		0.17	-0.18	-0.79	0	0.81
	9	1	3	4	1.55		0.11	0.22	0.03	-0.95	-0.72

Таблица 10 - Варианты заданий для решения дифференциальных уравнений

№ вар				№ вар
1	0	1	3	2	1	2	0
3	0	2	1	4	1	2	0
5	2	3	1	6	2	3	1
7	0		1	8	0	1	1
9	0	1	1/e	10	0	1	1/e
11	0	1	0	12	0	0.9	0
13	0	1	3	14	1	2	0
15	0	0.5	1	16	0	2	1
17	0	1	1	18	0	1	1
19	0	1	1	20	0		1

Таблица 11 –Варианты заданий для вычисления интегралов

№ варианта	Подинтегральная функция f(x)	Пределы интегрирования		№ варианта	Подинтегральная функция f(x)	Пределы интегрирования
№ варианта	Подинтегральная функция f(x)	a	b	№ варианта	Подинтегральная функция f(x)	a	b
1		1	3,5	2		1	4
3		0	1	4		0	2
5		1	2,5	6		0	3
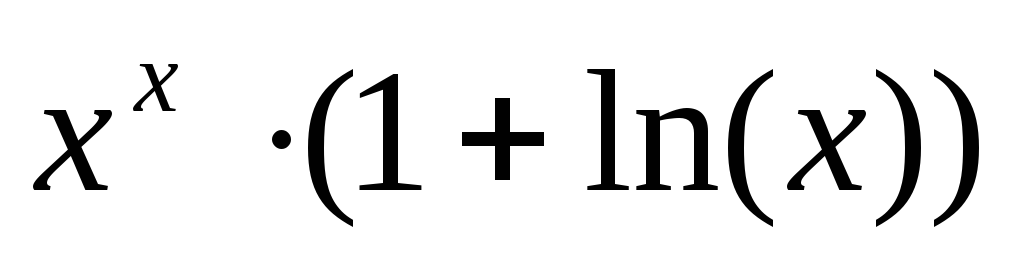
7		1	3	8		1	2
9		0	2	10		0	1,5
11		1	1,5	12		0	0,8
13		0	1	14		1	2
15		0	2	16		2	3
17		0	1,8	18		1	4
19		1	3	20		3	8

Таблица 12 - Варианты заданий для интерполяции и аппроксимации данных

x	y(x)	x	y(x)	x	y(x)	x	y(x)
1,0	0	2,0	4,62·10^-5	3,0	-0,00011	4,0	0,000196
1,1	0,324097	2,1	-0,44776	3,1	0,543966	4,1	-5,19505
1,2	0,643881	2,2	-0,87178	3,2	1,051358	4,2	-10,3689
1,3	0,922415	2,3	-1,2269	3,3	1,469572	4,3	-14,959
1,4	1,1253	2,4	-1,47335	3,4	1,753617	4,4	-18,4126
1,5	1,224745	2,5	-1,58114	3,5	1,870829	4,5	-20,25
1,6	1,20301	2,6	-1,53356	3,6	1,804553	4,6	-20,1243
1,7	1,054847	2,7	-1,3294	3,7	1,556275	4,7	-17,8711
1,8	0,788625	2,8	-0,98363	3,8	1,145949	4,8	-13,5425
1,9	0,425989	2,9	-0,52634	3,9	0,610438	4,9	-7,41942
5,0	0	6,0	0,001176	7,0	0,00018	8,0	-9,6·10^-5
5,1	8,037451	6,1	-11,4973	7,1	0,856485	8,1	-0,91714
5,2	15,89357	6,2	-22,5932	7,2	1,640842	8,2	-1,75557
5,3	22,72513	6,3	-32,1089	7,3	2,27459	8,3	-2,43156
5,4	27,73269	6,4	-38,9547	7,4	2,692863	8,4	-2,8763
5,5	30,25	6,5	-42,25	7,5	2,851227	8,5	-3,04297
5,6	29,82532	6,6	-41,4287	7,6	2,730379	8,6	-2,91168
5,7	26,2854	6,7	-36,3182	7,7	2,338403	8,7	-2,49175
5,8	19,77381	6,8	-27,1814	7,8	1,710348	8,8	-1,82115
5,9	10,75785	6,9	-14,7151	7,9	0,905108	8,9	-0,96308
9,0	-10^-13	10,0	0,000108	11,0	-0,00023	12,0	0,000357
9,1	0,97427	10,1	-1,02845	11,1	1,080087	12,1	-1,12952
9,2	1,863736	10,2	-1,96638	11,2	2,064282	12,2	-2,15806
9,3	2,579679	10,3	-2,72032	11,3	2,854531	12,3	-2,98314
9,4	3,049516	10,4	-3,21408	11,4	3,37121	12,4	-3,52184
9,5	3,224158	10,5	-3,3964	11,5	3,560925	12,5	-3,71872
9,6	3,083118	10,6	-3,24618	11,6	3,402017	12,6	-3,55153
9,7	2,636854	10,7	-2,77495	11,7	2,90698	12,7	-3,03371
9,8	1,926069	10,8	-2,02598	11,8	2,121544	12,8	-2,21331
9,9	1,01801	10,9	-1,07035	11,9	1,120452	12,9	-1,16858
13,0	-0,00055	14,0	0,000735	15,0	-0,00091	16,0	0,001095
13,1	0,447264	14,1	-0,54336	15,1	0,624825	16,1	-0,6968
13,2	0,871348	14,2	-1,05084	15,2	1,203832	16,2	-1,33944
13,3	1,226577	14,3	-1,46919	15,3	1,677044	16,3	-1,86182
13,4	1,473176	14,4	-1,75341	15,4	1,994648	16,4	-2,20969
13,5	1,581139	14,5	-1,87083	15,5	2,12132	16,5	-2,34521
13,6	1,533737	14,6	-1,80476	15,6	2,040105	16,6	-2,25098
13,7	1,329751	14,7	-1,55668	15,7	1,754519	16,7	-1,93222
13,8	0,984119	14,8	-1,14651	15,8	1,288629	16,8	-1,41658
13,9	0,526919	14,9	-0,61111	15,9	0,685062	16,9	-0,7518

Продолжение таблицы 12

x	y(x)	x	y(x)	x	y(x)	x	y(x)
17,0	-0,00128	18,0	0	19,0	-0,00059	20,0	0,000974
17,1	0,761981	18,1	-0,06906	19,1	0,328168	20,1	-0,49956
17,2	1,462508	18,2	-0,20633	19,2	0,661197	20,2	-0,98043
17,3	2,029831	18,3	-0,36975	19,3	0,95903	20,3	-1,38957
17,4	2,405585	18,4	-0,52416	19,4	1,183327	20,4	-1,67979
17,5	2,549509	18,5	-0,63728	19,5	1,301545	20,5	-1,8141
17,6	2,443738	18,6	-0,68247	19,6	1,29113	20,6	-1,77023
17,7	2,094918	18,7	-0,64188	19,7	1,142726	20,7	-1,54364
17,8	1,533913	18,8	-0,50883	19,8	0,86201	20,8	-1,14883
17,9	0,8131	18,9	-0,28908	19,9	0,46989	20,9	-0,6186

Варианты заданий для вычисления пределов функций, решения систем алгебраических уравнений, вычисления производных представлены в таблицах 13, 14 и 15 соответственно.

Таблица 13 –Варианты заданий для вычисления пределов функций

№ варианта	Вид функционального ряда	№ варианта	Вид функционального ряда
1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20

Таблица 14 –Варианты заданий для решения систем алгебраических уравнений

№ вар	Система уравнений	№ вар	Система уравнений
1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20

Таблица 15 –Варианты заданий для вычисления производной

№ вар	Функция	№ вар	Функция
1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20

Варианты заданий по моделированию линейных динамических систем в средах Matlab и Simulink представлены в таблице 16

Конкретный вид передаточных функций W1 – W5, выбирается из таблицы 2

Вид структурной схемы линейных динамических систем выбирается из рисунков 19- 28. Знак “--“, изображенный на рисунках означает отрицательную обратную связь. Значения коэффициентов передаточных функций (Таблицы 2 и 16) выбираются самостоятельно из следующих диапазонов апериодическое (А) – Т = 0.5… 2;

апериодическое второго порядка (А2) – Т₁= 0.5… 2; Т₂= 0.1.. 0.8; при колебательное (К) Т= 0.5… 2; ζ = 0.1… 0.9; дифференцирующее и дифференцирующее с запаздыванием (Д, ДЗ) Т= 0.1… 1; интегрирующее и интегрирующее с запаздыванием (И и ИЗ) Т= 0.05… 0.2;

Таблица 16 - Варианты заданий линейных динамических систем

№ вар	№ схемы	W1	W2	W3	W4	W5	Примечание
1	1	А	К	ДЗ	И	А
2	2	А2	А	ИЗ	И	А
3	3	К	А	ДЗ	А	И
4	4	А2	А	ДЗ	И	ИЗ
5	5	К	А	ДЗ	А	И
6	6	А	К	ИЗ	И	ИЗ
7	7	К	А	К	ИЗ	И
8	8	А2	К	А	И	А
9	9	К	ИЗ	А	И	У
10	10	А	А2	А	ИЗ	И
11	1	А2	К	И	ИЗ	И
12	2	К	А	ИЗ	А	И
13	3	А	К	А	ДЗ	И
14	4	К	А	ДЗ	И	ИЗ
15	5	А	К	А	ДЗ	И
16	6	К	А	ИЗ	И	А
17	7	А2	К	А	И	ИЗ
18	8	К	А2	А	А	И
19	9	К	А	ИЗ	И	А
20	10	К	А	А	И	ИЗ