4.Решение:

Записываем предложение ( ОБЯЗАТЕЛЬНО), в котором указываем, какой следует применить способ решения данной задачи: кинематический (поступательное, вращательное или более сложное движения, см. Табл. 3 и ЗНД, см. с.8); импульсный, силовой или энергетический, см. Табл. 4).

• Переписываем основную формулу из позиции 3 в векторном виде (кинематика поступательного движения, импульсный и силовой способы) или в скалярном виде (кинематика вращательного движения, энергетический способ, колебания) КОНКРЕНТНО для данной задачи. Это или упростит уравнение, записанное в позиции 3, (см. Пример 1.1.) или раскроет общее выражение (см. Пример 1.2)

• Проецируем векторное уравнение (или уравнения) на оси ox и oy (для скалярных величин этого, конечно, делать не надо):

Пр. ox : ….

Пр. oy : ….

Решаем полученную систему уравнений, используя дополнительные формулы из позиции 3.

• Записываем окончательную формулу в БУКВЕННОМ виде (здесь должно быть только одно выражение).

• Проверяем единицы измерения (см. схему расположения позиций алгоритма решения задач).

• Подставляем цифровые значения (если они заданы).

Когда в задаче даны 2 тела, то следует записать в п. 1) систему двух уравнений, то же необходимо сделать при решении кинематических задач (даже для одного тела), например:

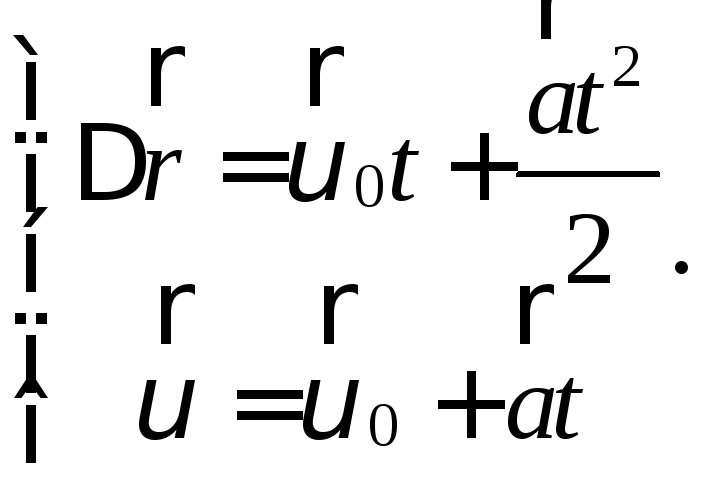
Если в задаче требуется найти значения двух или более физических величин ( а) и б) ), то для каждого случая необходимо повторить действия согласно Решению ( пункты 1), 2), 3), 4), 5) ).

При проверке единиц измерения полезно использовать позицию 5. Преобразование единиц измерения. См. Пример 1.3.

5.Преобразование единиц

измерения:

Схема алгоритма решения задач.

1. Дано: 2. Рисунок: 3.Используемые

формулы:

4. Решение

Записываем, каким способом предполагается решать или начинать решение данной задачи .

1)

2) 5. Преобразование

3) единиц измерения:

4)

5)

В позиции 5 производим промежуточные преобразования единиц измерения, входящие в пункт 4) позиции 4( Решение).

Алгоритм преобразования единиц измерения (позиция 5)

а) Записать формулу (наиболее простую) в общем виде (например, N = A / t).

б) Записать ее в соответствии с правилом определения единиц измерения

([N]=[A]/[t]).

в) При необходимости произвести промежуточные преобразования единиц измерения (позиция 5.) ([A]=[F][S]).

г) Результаты, полученные в п.п. в) перенести в формулу п.п. б).

( [N]=[F][S] / [t].)

д) Подставить единицы измерения ( [N]=(Н*м)/с=Дж/с=Вт.)

Примеры:

1. Проверить справедливость формулы для расчета первой космической скорости .

а) . Более удобно представить эту формулу в следующем виде:

б)

в ) Произвести промежуточное преобразование единиц измерения (по-

зиция 5.) для G, используя закон Всемирного тяготения и второй закон Ньютона. Результат перенести в п.п. г )

Г) 5. Преобразование единиц измерения:

Д)

;

;

;

.

2. Допустим, в пунктах 3) и 4) решения имеем следующие формулы (см. также пример 2.5.):

3) 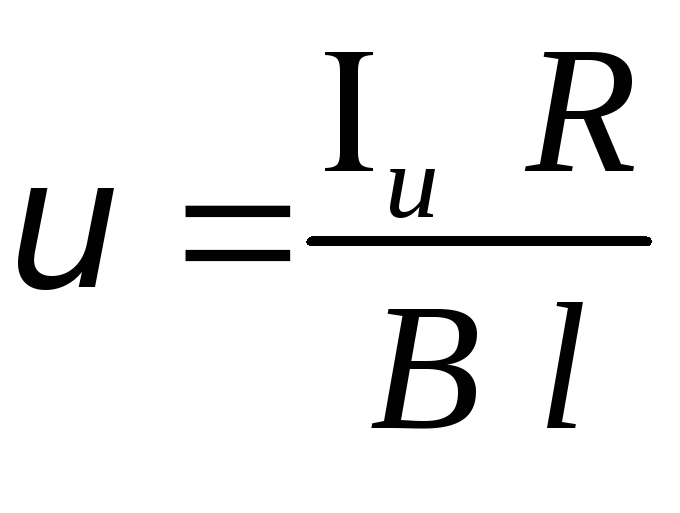5.Преобразование единиц измерения:

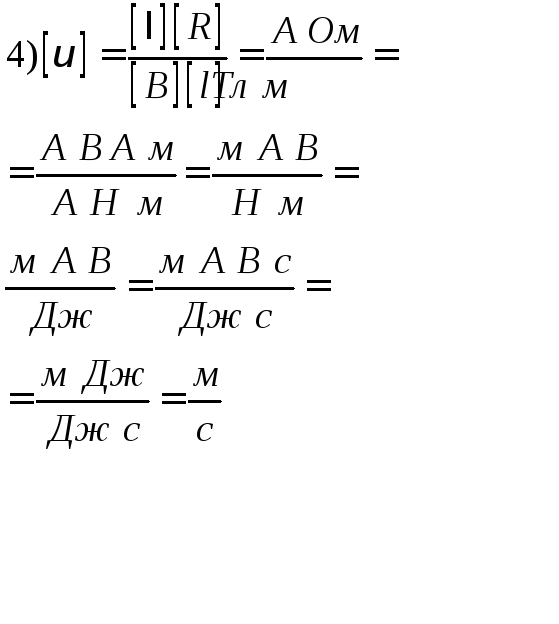
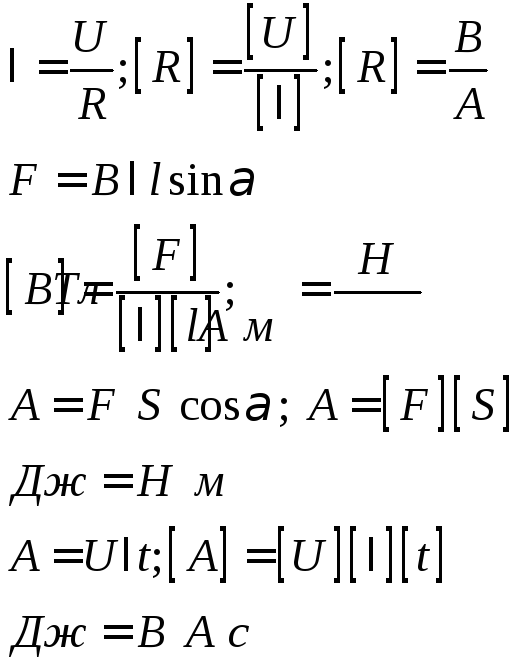
Примечание. Здесь для удобства вычислений были домножены числитель и знаменатель на « с ».

Примеры решения задач

1.1 Мяч бросают со скоростью ₀=54км/ч под углом к горизонту α=30⁰. Найти дальность S_х полета мяча и его скорость _А в высшей точке.

1. Дано: 2.Рисунок: 3 Используемые формулы:

ϑ₀=54км/ч=15м/с

α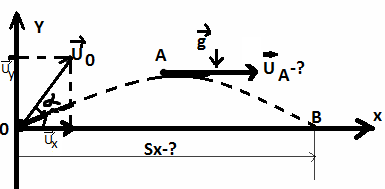=30⁰=

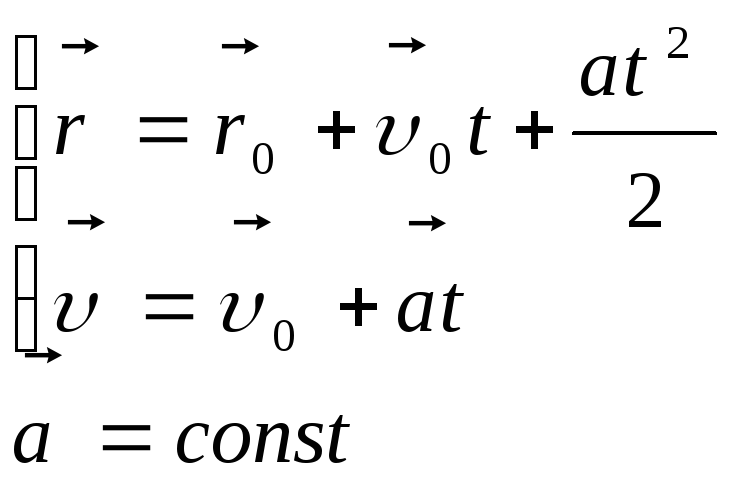
а) S_х-?

б) - ? ……

4. Решение:

Для решения задачи используем закон независимости движений (З.Н.Д.) и кинематический способ (поступательное равнопеременное движение).

а) 1)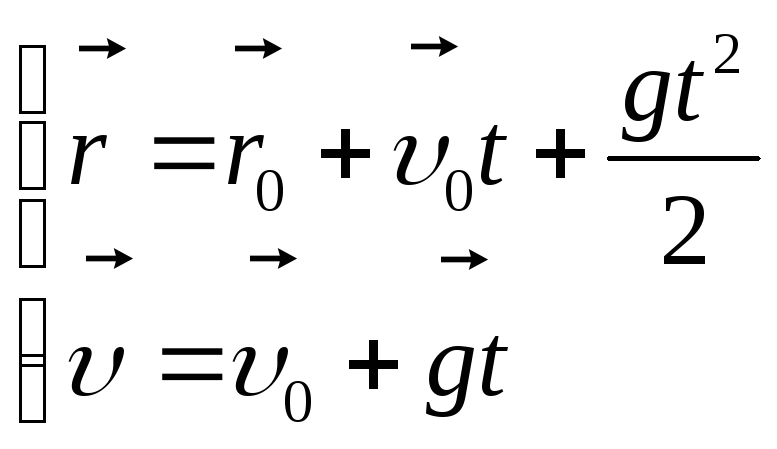,, т.к. начало системы

отсчета (точка 0) совпадает с начальным положением мяча. Как видим, при переписывании формул из позиции 3 конкретно для данной задачи мы значительно их упростили.

2) Пр. на ось x:

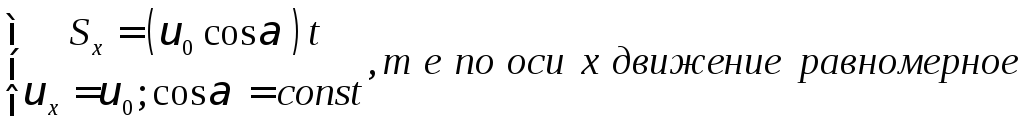
Пр. на ось y: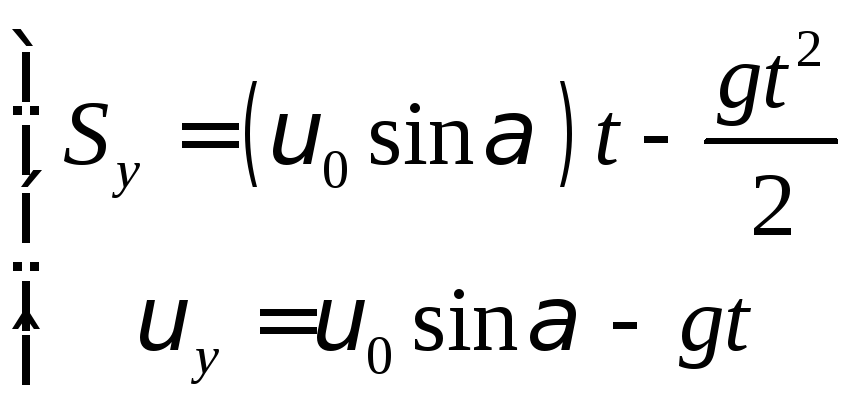

Прежде, чем определять S_х из третьего уравнения системы найдем полное время полета мяча t:

О=(₀ sin) t- (S_у в точке В равно 0),

t = , S_х= .

3) S_х=;

4) [S] = ==м.

5) S_х==20 м.

б) 1) Для нахождения используем четвертое уравнение системы

2) 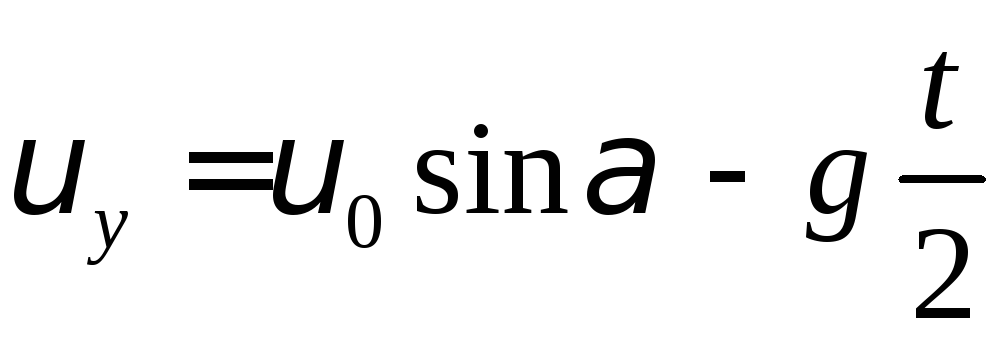| (т.к. время подъема мяча в два раза меньше полного времениt).

Подставляя найденное ранее значение t, получаем = sinα - sin=0 – в точке А движения по осинет.

По теореме Пифагора полная скорость в любой точке траектории

, поэтому .

3) ==₀ cosα= const (т.е. в точке А движение равномерное)

4) [] = м/c.

5) =15.0,5=7,5 м/с.

1.2 Санки скатываются по ледяной горке длинойи углом наклона. На какое расстояниеот подножия откатятся санки, если коэффициент трения на заснеженном горизонтальном участке -.

1

.Дано: 2.Рисунок: 3. Используемые формулы: