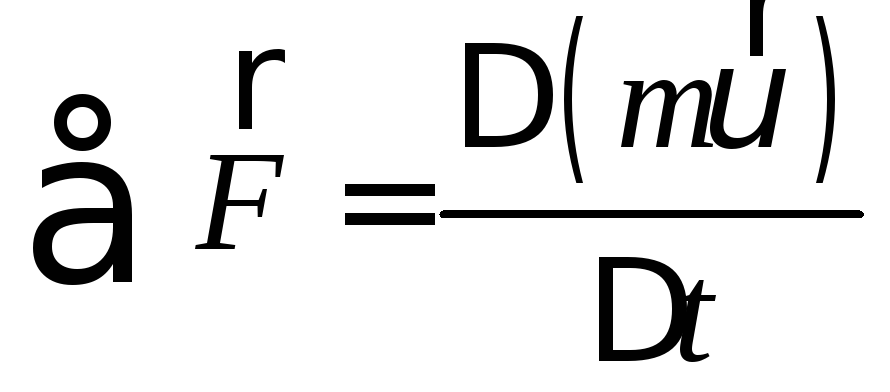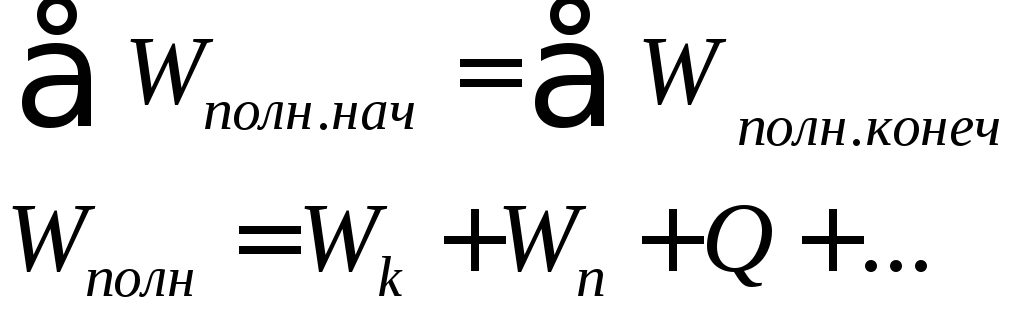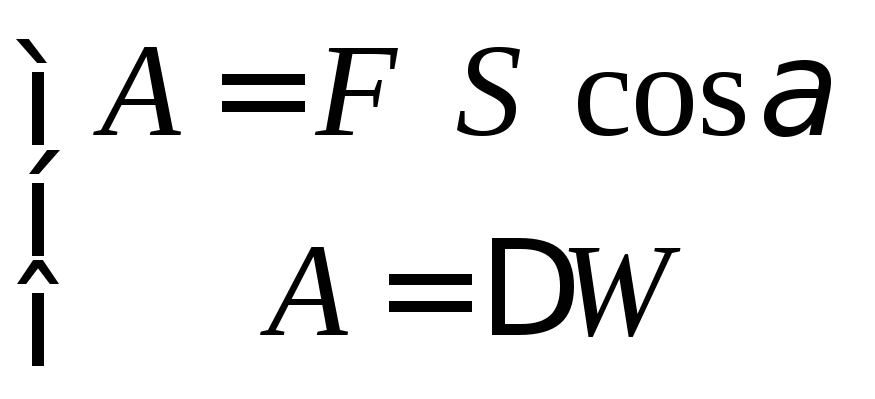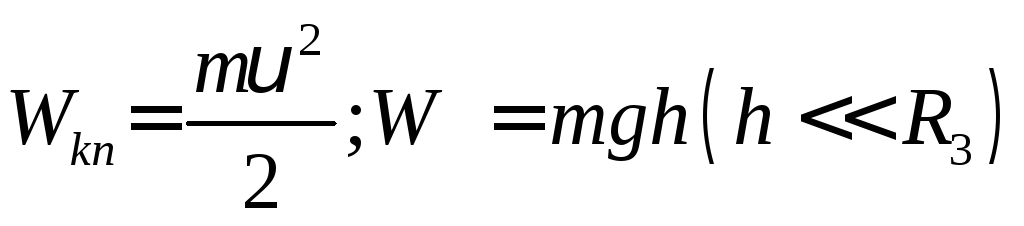Динамика поступательного движения

Импульсный способ	Силовой способ	Энергетический способ
Закон сохранения импульса:	Второй закон Ньютона , (m=const) ∑–уравнение движения(m=сonst)	а) Закон сохранения мех. энергии: б) Закон Ломоносова: (Q – количество теплоты)
	=μN F(.)=G(закон Всемирного тяготения) Данную колонку можно продолжить при изучении электромагнетизма и др.
Изменение импульса:
		в)
		(при гравитационном взаимодействии материальных точек) (при упругой деформации)

1.3 Механика твердого тела.

В этом разделе вводятся новые физические величины: момент инерции J, момент импульса , момент силы.

При решении задач на вращательное движение полезно пользоваться следующей таблицей: Таблица 5

Взаимосвязь поступательных и вращательных физических величин.

Поступательные физ. величины	Вращательные физ. величины	Взаимосвязь

Эту таблицу удобно использовать при решении задач, если студент забыл какую – то формулу вращательного движения. Например, чтобы перейти от второго закона Ньютона к основному уравнению вращательного движения, поступаем так: записываем второй закон Ньютона: Из таблицы 5 следует: т.е.

Студентам предлагается, используя таблицы 4 и 5, составить (по аналогии) таблицу 6 «Динамика вращательного движения абсолютно твердого тела».

1.4 Методика решения задач по механике.

Во-первых, необходимо выяснить, к какому разделу физики относится данная задача: к кинематике или динамике. Во-вторых, какой следует применить способ решения.

Как уже упоминалось, существует 5 основных способов решения механических задач: кинематический (поступательное и вращательное движения), импульсный, силовой и энергетический.

Формулы, необходимые для решения этих задач, приведены в табл.1-5.

Чтобы придать решению задач более строгий и понятный вид, студентам предлагается использовать ниже приведенный Алгоритм (см. с.14).

Кроме того, следует придерживаться следующих требований, предъявляемых к решению задач по физике (не только механических).

• Выписать условие задачи в колонку в принятом стандартном буквенном и числовом обозначениях. Если необходимо обозначить несколько сходных величин, можно ввести большие и малые буквы или численные индексы.

• Все величины, приведенные в условии задачи, выразить в интернациональной системе единиц (СИ).

• Вспомнить физические законы, на основании которых должно проводиться решение задачи. Дать формулировку этих законов.

• Сделать чертеж (рисунок, график, схему), поясняющий содержание задачи. Например, изобразить тело с приложенными к нему силами, схему электрической цепи и т. п.

• Решение большинства задач сводится к составлению алгебраических уравнений, отражающих заданный физический процесс. Поэтому задачи необходимо доводить до конца не в численном, а в буквенном виде. При таком способе ответ получается в виде формулы, которая позволяет проверить полученный результат.

(Не следует смущаться, если в уравнения войдут величины, не заданные в условии задачи. Такие величины, как правило, или исключаются при алгебраических выкладках, или они могут быть найдены в справочных таблицах).

• Получив ответ в виде алгебраической формулы, надо произвести проверку единиц измерения, т.е. убедиться, что эти единицы в правой и левой частях равенства совпадают ( см. табл.1).

• Подставить в формулу числовые значения величин, приведенных в условиях задачи. При арифметических расчетах следует использовать правила приближенных вычислений и производить расчеты лишь с тем количеством значащих цифр, которое определяется условиями задачи.

• Необходимо обратить внимание на численное значение конечного результата задачи. Так, например, если коэффициент полезного действия больше 100% , значит, была допущена ошибка.

Алгоритм решения задач

1. Дано: 2.Рисунок : 3.Используемые формулы:

Перевод в Си Основная формула

а) - ? Дополнительные

б) - ? формулы