Лабораторная работа №5

Обработка многомерных массивов. Сложные циклы

Теоретическая часть

Сложные циклы

Циклы называются вложенными или сложными, если телом цикла является циклическая структура. Цикл, содержащий в себе другой цикл, называется внешним, а цикл, содержащийся в теле другого цикла, называется внутренним.

Внутренний и внешний циклы могут быть любого вида: циклами с параметром, с предусловием или с постусловием. При работе с многомерными массивами чаще всего используются циклы с параметром.

Для циклов с параметром параметры внешнего и внутреннего циклов изменяются не одновременно, т.е. при фиксированном значении параметра внешнего цикла параметр внутреннего цикла последовательно принимает все возможные значения. После этого параметр внешнего цикла изменяется на шаг, выполняется внутренний цикл и т.д. При организации вложенных циклов необходимо следить за тем, чтобы все операторы внутреннего цикла полностью лежали в теле внешнего цикла.

Многомерные массивы

В одномерных массивах компонентами являются скалярные значения, т.е. отдельные данные. Компонентами массива могут быть массивы. Если компоненты-массивы состоят из скалярных значений, то получается двумерный массив, называемый матрицей. Если компонентами массива являются матрицы, то получаем трехмерный массив. По аналогии можно определить массив любой размерности. При объявлении массивов в Delphi имеется ограничение: размер памяти, занимаемый массивом не должен превышать 2 Гбайта. Разрешается использовать массивы до семимерных включительно.

Возможный вид задания двумерного массива вещественных чисел A_10×20 :

Type matr = array [1..10] of array [1..20] of real;

Var A:matr;

или

Type matr = array [1..10,1..20] of real;

Var A:matr;

Индексная переменная A_ij может быть записана в форме A[i][j] или A[i,j] и обозна­чает элемент матрицы, расположенный на пересечении i-той строки и j-того столбца.

Для задания значений элементам матрицы в данной работе следует использовать поэлементный ввод. Например, для ввода матрицы A_m×n можно записать

For i:=1 to m do

For j:=1 to n do

begin

write(‘a[‘,i,’,’,j,’]=’);

readln(a[i,j])

end;

Фрагмент программы для вывода матрицы A_m×n на экран в виде таблицы можно записать так:

Writeln(‘Matrica A‘:12);

For i:=1 to m do

begin

For j:=1 to n do write(a[i,j]:8:2);

writeln

end;

Примеры

Приведем несколько примеров реализации простейших заданий.

Пример №1. Вычислить сумму элементов матрицы A_m×n .

S:=0;

For i:=1 to m do

For j:=1 to n do s:=s+ a[i,j];

Пример №2. Вычислить сумму элементов каждого столбца матрицы A_m×n .

For j:=1 to n do

begin

s[j]:=0;

For i:=1 to m do s[j]:=s[j]+a[i,j]

end;

Пример №3. Поменять местами первую и последнюю строки матрицы A_m×n .

For j:=1 to n do

begin

b:=a[1,j]; a[1,j]:=a[m,j]; a[m,j]:=b

end;

Пример №4. Удалить k-тый столбец матрицы A_m×n .

For j:=k to n-1 do

For i:=1 to m do a[i,j]:= a[i,j+1];

Пример №5. Вычислить сумму элементов главной диагонали и сумму элементов, расположенных выше главной диагонали, квадратной матрицы A_m×m .

Sd:=0; Sv:=0;

For i:=1 to m do Sd:=Sd+ a[i,j];

For i:=1 to m-1 do

For j:=i+1 to m do Sv:=Sv+ a[i,j];

Задания к работе

Разработать программу и тестовый пример для проверки работы программы.

I уровень

1. Задана квадратная матрица A_m×m . Найти в каждой строке наибольший элемент и поменять его местами с элементом главной диагонали.

2. В заданной квадратной матрице порядка n к каждому элементу главной диагонали прибавить сумму предшествующих ему элементов данной строки.

3. В заданной матрице A_m×n найти минимаксный элемент и номер строки, в которой он расположен. Минимаксным элементом матрицы называется минимальный из максимальных элементов строк.

4. В заданной матрице A_m×n строку, содержащую максимальный элемент, поменять местами со строкой, содержащей минимальный элемент. Предполагается, что эти элементы единственны.

5. В каждом столбце заданной матрицы A_m×n найти наибольший по модулю элемент и вычислить сумму истинных значений найденных элементов.

6. Задана матрица A_m×m . Сформировать одномерный массив B размером n из ±1, в котором j-тый элемент равен -1, если j-том столбце матрицы есть хотя бы один отрицательный элемент, и +1 – в противном случае.

7. Задана матрица A_m×m . Сформировать одномерный массив B размером m по правилу: элемент b_i получает значение первого по порядку положительного элемента i-той строки, а, если таких элементов нет, то b_i =-1.

8. Задана матрица A_m×m . Сформировать одномерный массив B размером m из 1 и 0, в котором b_i =1, если в i-той строке матрицы нет нулевых элементов, и b_i =0 – в противном случае.

9. Задана квадратная матрица A_n×n . Сформировать одномерный массив B размером n по правилу: если элемент A_ii отрицателен, то в качестве b_i принять сумму элементов i-той строки, предшествующих диагональному элементу, а если A_ii неотрицателен, то в качестве b_i принять сумму элементов i-той строки, следующих за диагональным элементом, включая его.

10. В заданной квадратной матрице порядка n все элементы, находящиеся над главной диагональю, разделить на наибольший по модулю элемент, расположенный на главной диагонали.

11. Задана квадратная матрица A_n×n , целые k и m (1≤k≤n, 1≤m≤n). Преобразовать матрицу следующим образом: строку с номером k сделать столбцом с номером m, а столбец с номером m сделать строкой с номером k.

12. Задана матрица A_m×m . Определить, есть ли в ней строки, все элементы которых равны нулю, за исключением последнего. Вывести на экран номера таких строк или информацию об их отсутствии.

13. В заданной матрице A_m×n провести циклическую перестановку столбцов: второй поставить на место первого, третий – на место второго и т.д. Первый столбец должен занять место последнего.

14. В заданной матрице A_m×n провести циклическую перестановку столбцов: первый поставить на место второго, второй – на место третьего и т.д., а последний – на место первого.

15. В заданной матрице A_m×n провести циклическую перестановку строк, начиная с k-той и кончая последней. При этом (k+1)-ая строка должна занять место k-той, (k+2)-ая строка – место (k+1)-ой и т.д., последняя строка – место предпоследней, а k-ая строка должна стать последней.

II уровень

1. Задана матрица A_m×m и одномерный массив B размером m. Элементы 1-го столбца матрицы упорядочены по убыванию. Включить массив B в качестве новой строки матрицы с сохранением упорядоченности по элементам 1-го столбца.

2. Задана матрица A_m×n . Найти максимальный по модулю элемент матрицы. Переста­вить строки и столбцы матрицы таким образом, чтобы максимальный по модулю элемент был расположен на пересечении 1-й строки и 1-го столбца.

3. Задана квадратная матрица A_n×n . Исключить из нее строку и столбец, на пересечении которых расположен максимальный по модулю элемент главной диагонали.

4. Из заданной матрицы A_m×n исключить строки, содержащие хотя бы один нулевой элемент.

5. Задана матрица A_m×m . Вывести на экран индексы какой либо седловой точки матрицы или информацию об отсутствии такой точки в матрице. Седловой точкой называется элемент матрицы, который является одновременно наименьшим в своей строке и наибольшим в своем столбце.

6. Задана матрица A_m×m , одномерный массив B размером m и одномерный массив C размером n+1. Добавить в матрицу слева столбец, совпадающий с массивом B, а сверху строку, совпадающую с массивом C, предварительно сдвинув 1-й и последующие столбцы на одну позицию вправо, а 1-ю и последующие строки на одну позицию вниз.

7. Задана матрица A_m×m . Сформировать матрицу B из тех строк матрицы A, которые не содержат нулевых элементов.

8. Задана матрица A_m×m . Сформировать матрицу B из тех столбцов матрицы A, которые содержат хотя бы один отрицательный элемент.

9. В заданной матрице A_m×n упорядочить по возрастанию элементы каждой строки.

10. Задана матрица A_m×m . Упорядочить (переставить) строки матрицы по возрастанию сумм их элементов.

11. Задана матрица A_m×m . Упорядочить (переставить) столбцы матрицы по возрастанию сумм их элементов.

12. В заданной матрице A_m×n найти строку с максимальной суммой модулей элементов.

13. Задана квадратная матрица A_n×n . Вычислить скалярное произведение строки и столб­ца (рассматриваемых как векторы), на пересечении которых находится минимальный элемент матрицы.

Указание. Скалярное произведение векторов x и y размером n вычисляется по формуле

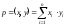
14. Определить, является ли заданная квадратная матрица ортонормированной, т.е. такой, в которой скалярное произведение различных строк равно 0, а скалярное произведение строки на себя равно 1.

15. Из заданной матрицы A_m×n удалите повторяющиеся строки, если они есть.

Дополнительные задачи

1. Найти максимальное из чисел, встречающихся в заданной матрице A_m×n более одного раза.

2. Задан массив a₁, a₂, ..., a_n . Сформировать из него матрицу B, содержащую по k элементов в строке. Недостающие элементы в последней строке (если такие будут) заполнить нулями. Вывести на экран полученную матрицу.

3. Задана квадратная матрица A_n×n . Сформировать массив b₁, b₂, ..., b_2n-1 , i-тый элемент которого равен сумме элементов матрицы A, расположенных на i-той диагонали, параллельной главной диагонали. Нумерация диагоналей, параллельных главной, начинается с левого нижнего элемента матрицы.

4. Сформировать целочисленную квадратную матрицу порядка n, элементами которой являются числа 1, 2, 3, ..., n², расположенные в ней по спирали по часовой стрелке, начиная с левого верхнего угла.

5. Задана квадратная матрица A_n×n (n=2k+1 – нечетно). Начиная с центра, обойти по часовой стрелке по спирали все элементы этой матрицы, распечатывая их в порядке обхода.