
Лекции по физике / 2.2.Термодинамика-1гр
.doc§ 2.2. Законы термодинамики
Термодинамика – это учение о связи и взаимопревращениях различных видов энергии, теплоты и работы.
Термодинамика основывается на нескольких фундаментальных законах, называемых началами термодинамики, установленных на основании обобщения большого числа опытных данных.
Введём основные величины, используемые в термодинамике.
1.
Внутренняя энергия тела включает в себя
кинетическую энергию хаотического
движения молекул, потенциальную энергию
взаимодействия молекул, энергию
электронных оболочек атомов и ионов,
энергию движения и взаимодействия
нуклонов в атомных ядрах. Обозначается
внутренняя энергия
![]() и измеряется в джоулях (Дж). Внутренняя
энергия системы тел равна сумме внутренних
энергий каждого из тел и энергии их
взаимодействия.
и измеряется в джоулях (Дж). Внутренняя
энергия системы тел равна сумме внутренних
энергий каждого из тел и энергии их
взаимодействия.
Внутренняя энергия – функция состояния системы. Это значит, что:
-
Всякий раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее этому состоянию значение независимо от предыстории системы.
-
Изменение внутренней энергии системы при переходе из одного состояния в другое всегда равно разности значений внутренней энергии в этих состояниях и не зависит от пути, по которому совершался этот переход, т.е. не зависит от процессов, приведших к переходу из одного состояния в другое.
-
Если в результате какого-либо процесса система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю.
Внутренняя энергия системы зависит от температуры и фазового состояния системы.
Изменение внутренней энергии системы может осуществляться двумя способами: путем совершения работы и путем теплообмена.
2.
Количество теплоты
![]() - это энергия, отдаваемая или получаемая
в процессе теплопередачи.
- это энергия, отдаваемая или получаемая
в процессе теплопередачи.
![]() .
.
Количество
переданной теплоты
![]() и величина совершенной работы
и величина совершенной работы
![]() зависит от вида процесса при переходе
системы из одного состояния в другое,
т.е. от того, через какие промежуточные
состояния проходит система.
зависит от вида процесса при переходе
системы из одного состояния в другое,
т.е. от того, через какие промежуточные
состояния проходит система.
Тепловые свойства тел, характеризуются теплоемкостью.
Теплоемкость
тела – это отношение сообщаемой телу
теплоты
![]() к соответствующему изменению температуры
тела
к соответствующему изменению температуры
тела
![]()
![]() .
.
Измеряется теплоемкость тела в Дж/К и зависит от массы тела, химического состава тела, от температуры и от вида процесса.
Удельная
теплоемкость
![]() – величина, численно равная количеству
теплоты, которое нужно сообщить единице
массы вещества для изменения его
температуры на 1К в рассматриваемом
термодинамическом процессе
– величина, численно равная количеству
теплоты, которое нужно сообщить единице
массы вещества для изменения его
температуры на 1К в рассматриваемом
термодинамическом процессе
![]() ,
,
![]() - масса тела. Единицей измерения
- масса тела. Единицей измерения
![]() в СИ является Дж/кг·К.
в СИ является Дж/кг·К.
Молярная
теплоемкость
![]() численно равна количеству теплоты,
которое нужно сообщить 1молю вещества
для изменения его температуры на 1К в
данном термодинамическом процессе
численно равна количеству теплоты,
которое нужно сообщить 1молю вещества
для изменения его температуры на 1К в
данном термодинамическом процессе
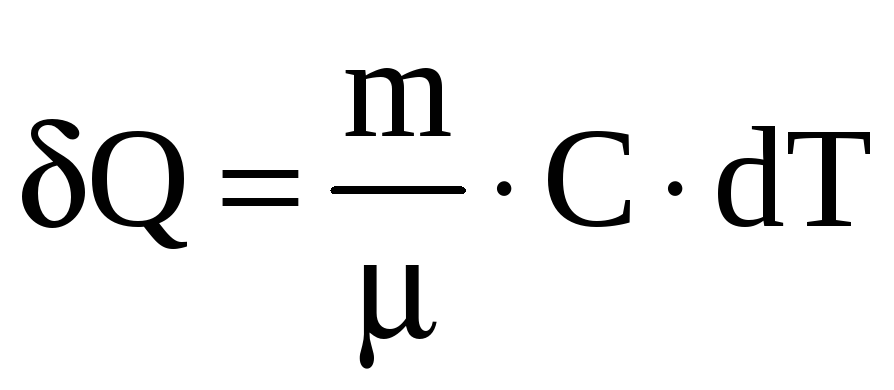 .
Единицей измерения
.
Единицей измерения
![]() в СИ является Дж/моль·К.
в СИ является Дж/моль·К.
![]() - молярная масса.
- молярная масса.
Удельная
и молярная теплоемкости связаны друг
с другом соотношением
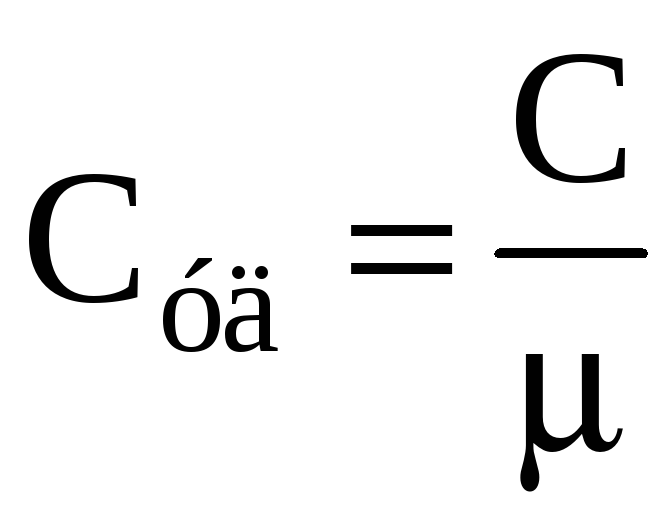 .
.
3 .
Работа, совершаемая газом при расширении.
Пусть газ находится в сосуде под поршнем
площадью
.
Работа, совершаемая газом при расширении.
Пусть газ находится в сосуде под поршнем
площадью
![]() .
Сила, с которой газ действует на поршень
.
Сила, с которой газ действует на поршень
![]() .
Элементарная работа, совершаемая газом
при перемещении поршня на величину
.
Элементарная работа, совершаемая газом
при перемещении поршня на величину
![]()
![]() ,
где
,
где
![]() - изменение объема газа. При конечных
изменениях объема тела
- изменение объема газа. При конечных
изменениях объема тела
 .
.
Е сли
система переходит из состояния 1 в
состояние 2. Элементарная работа
сли
система переходит из состояния 1 в
состояние 2. Элементарная работа
![]() измеряется площадью заштрихованной
полоски. Полная работа, совершаемая
системой за весь процесс, измеряется
площадью, ограниченной кривой 1-2, осью
OV
и графиками
измеряется площадью заштрихованной
полоски. Полная работа, совершаемая
системой за весь процесс, измеряется
площадью, ограниченной кривой 1-2, осью
OV
и графиками
![]() и
и
![]() .
.
1-е
начало термодинамики: Количество
теплоты, сообщенное системе, расходуется
на изменение внутренней энергии системы
и на совершение системой работы против
внешних сил
![]() .
.
Здесь
![]() - полный дифференциал, т.к. при совершении
любого процесса, в результате которого
система возвращается в исходное
состояние, изменение ее внутренней
энергии равно нулю
- полный дифференциал, т.к. при совершении
любого процесса, в результате которого
система возвращается в исходное
состояние, изменение ее внутренней
энергии равно нулю
![]() .
Теплота и работа таким свойством не
обладают, поэтому
.
Теплота и работа таким свойством не
обладают, поэтому
![]() и
и
![]() не являются полными дифференциалами.
не являются полными дифференциалами.
С
учетом полученных формул для работы и
теплоты 1-е начало термодинамики можно
записать в виде
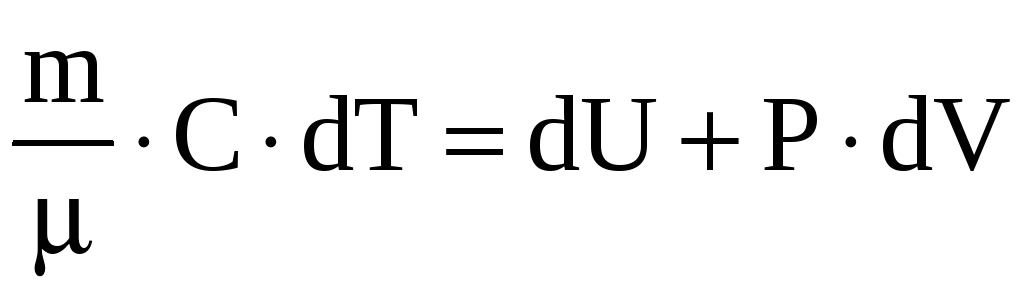 .
.
Применим 1-е начало термодинамики к изопроцессам.
-
Изохорный процесс
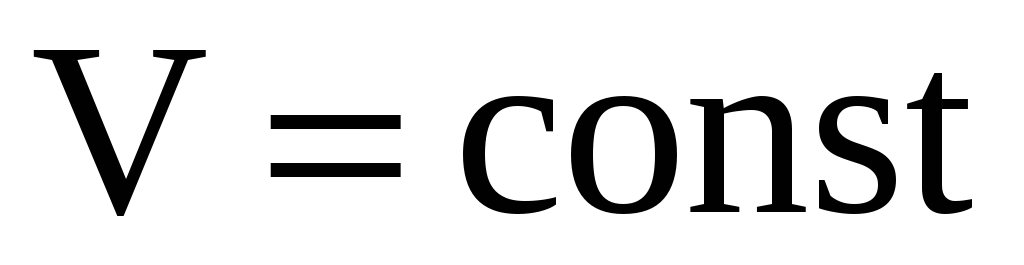 .
.
Осуществляется
изохорный процесс при нагревании или
охлаждении газа в сосуде постоянного
объема. Изменение объема газа
![]() .
Следовательно,
.
Следовательно,
![]() ,
т.е. в этом процессе газ не совершает
работы. В этом случае из 1-го начала
термодинамики следует, что вся теплота,
сообщаемая газу, идет на изменение его
внутренней энергии
,
т.е. в этом процессе газ не совершает
работы. В этом случае из 1-го начала
термодинамики следует, что вся теплота,
сообщаемая газу, идет на изменение его
внутренней энергии
![]() .
Таким образом,
.
Таким образом,
 ,
где
,
где
![]() - молярная теплоемкость газа при
постоянном объеме.
- молярная теплоемкость газа при
постоянном объеме.
Приращение
внутренней энергии газа при изменении
его температуры от
![]() до
до
![]()
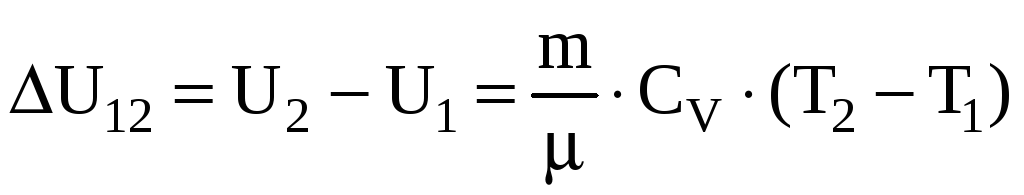 .
Соответственно теплота, сообщаемая
газу
.
Соответственно теплота, сообщаемая
газу
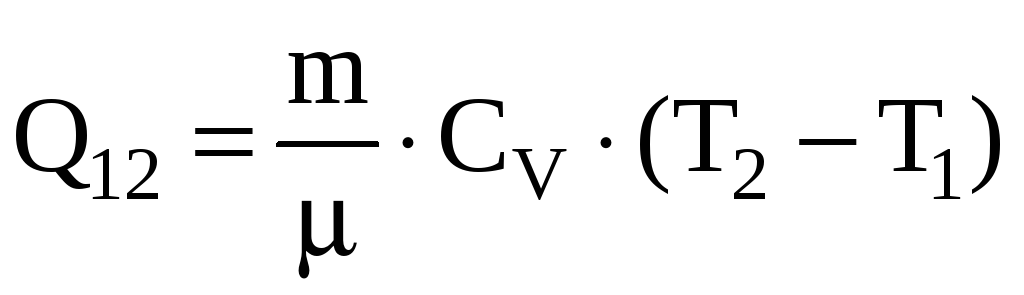 .
.
-
Изобарный процесс
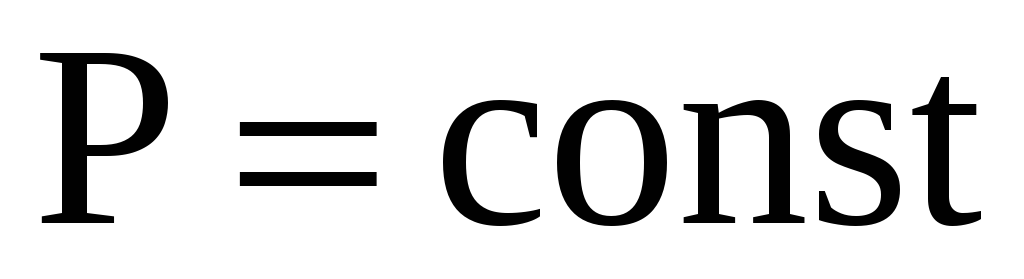 .
.
Осуществляется
изобарный процесс при нагревании или
охлаждении газа в цилиндре с подвижным
поршнем, на который действует постоянное
внешнее давление. Элементарное количество
теплоты, сообщаемое газу в изобарном
процессе
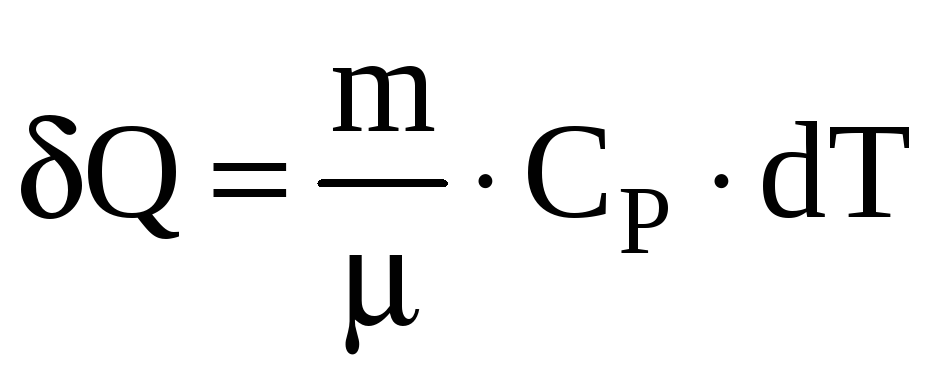 ,
где
,
где
![]() - молярная теплоемкость газа при
постоянном давлении.
- молярная теплоемкость газа при
постоянном давлении.
 .
Элементарная работа, совершаемая газом
в изобарном процессе
.
Элементарная работа, совершаемая газом
в изобарном процессе
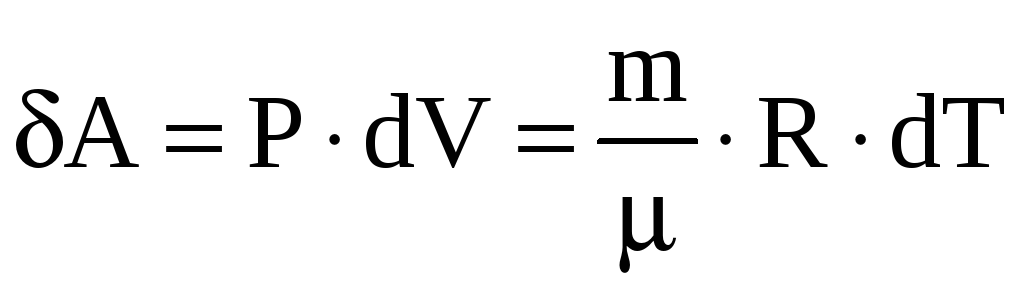 (из уравнения Менделеева-Клапейрона
при
(из уравнения Менделеева-Клапейрона
при
![]() следует, что
следует, что
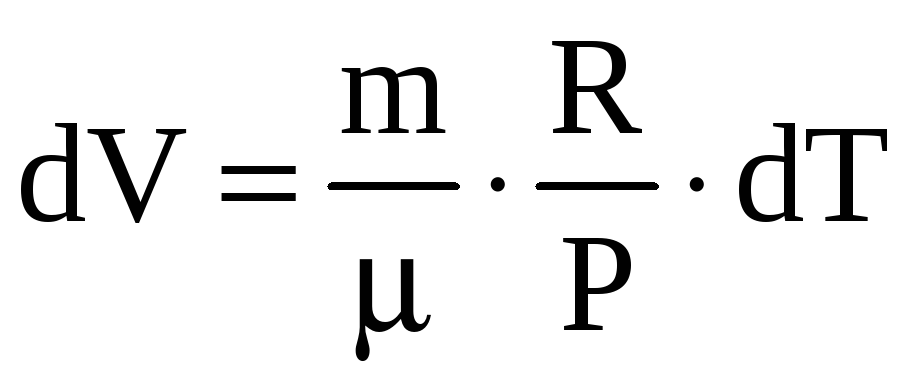 ).
В этом случае 1-е начало термодинамики
).
В этом случае 1-е начало термодинамики
 ,
и после сокращения
,
и после сокращения
![]() .
Это уравнение Майера. Оно выражает связь
между теплоемкостями идеального газа
при постоянном давлении и при постоянном
объеме.
.
Это уравнение Майера. Оно выражает связь
между теплоемкостями идеального газа
при постоянном давлении и при постоянном
объеме.
![]() ,
т.к. в изобарном процессе, в отличие от
изохорного, теплота, сообщаемая газу,
расходуется не только на изменение
внутренней энергии, но и на совершение
работы.
,
т.к. в изобарном процессе, в отличие от
изохорного, теплота, сообщаемая газу,
расходуется не только на изменение
внутренней энергии, но и на совершение
работы.
Работа,
совершаемая газом при изобарном процессе
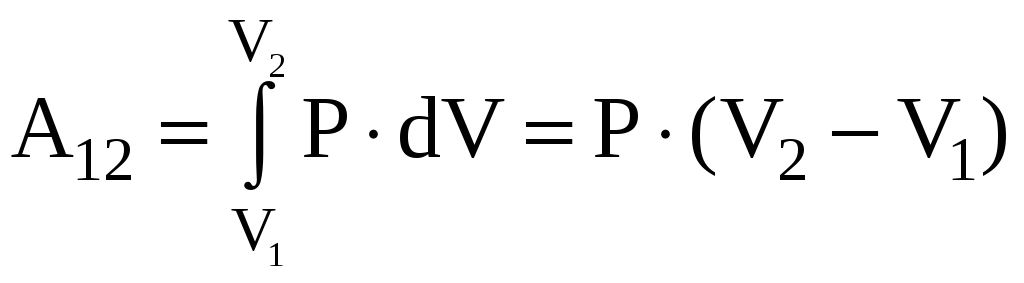 .
Теплота, сообщается газу в изобарном
процессе
.
Теплота, сообщается газу в изобарном
процессе
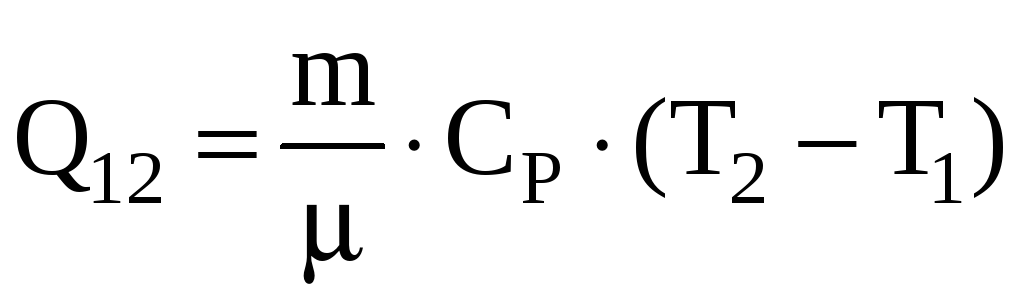 .
.
-
Изотермический процесс
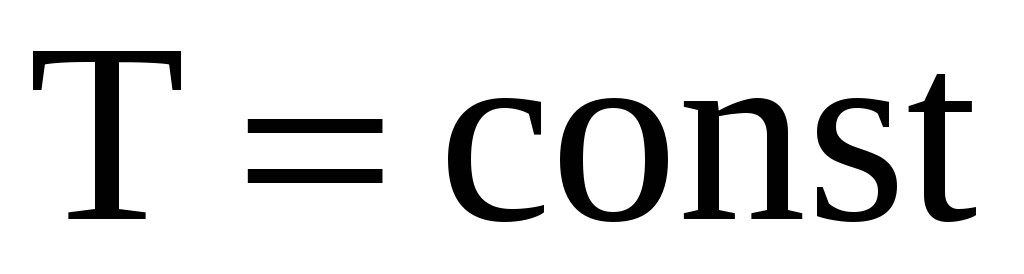 .
.
Поскольку
![]() ,
то
,
то
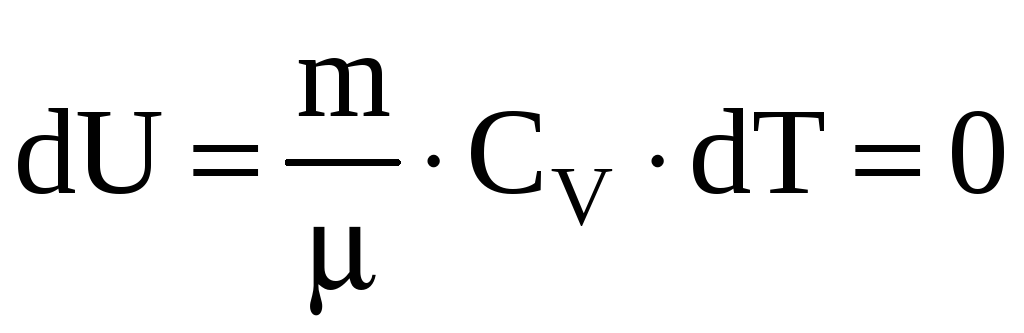 ,
т.е. внутренняя энергия газа не изменяется
при изотермическом процессе. Следовательно,
,
т.е. внутренняя энергия газа не изменяется
при изотермическом процессе. Следовательно,
![]() ,
т.е. вся теплота, сообщенная газу,
расходуется на совершение газом работы
против внешних сил.
,
т.е. вся теплота, сообщенная газу,
расходуется на совершение газом работы
против внешних сил.
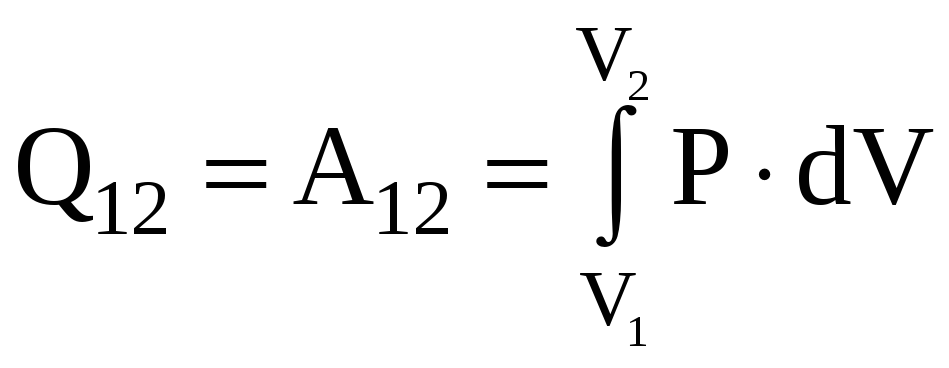 .
Подставим в это уравнение давление,
выраженное из уравнения Менделеева-Клапейрона,
.
Подставим в это уравнение давление,
выраженное из уравнения Менделеева-Клапейрона,
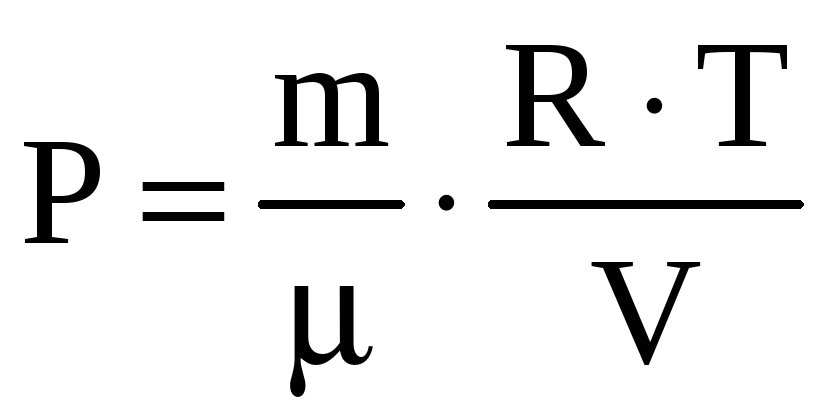 .
Получим
.
Получим
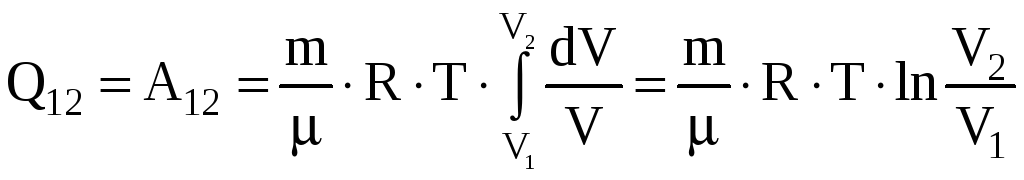 .
При расширении газа
.
При расширении газа
![]() ,
работа, совершаемая газом
,
работа, совершаемая газом
![]() .
Это означает, что для расширения газа
при постоянной температуре к газу нужно
подводить тепло
.
Это означает, что для расширения газа
при постоянной температуре к газу нужно
подводить тепло
![]() .
При сжатии газа
.
При сжатии газа
![]() работа, совершаемая газом
работа, совершаемая газом
![]() .
Это означает, что для изотермического
сжатия газа от газа нужно отводить
тепло.
.
Это означает, что для изотермического
сжатия газа от газа нужно отводить
тепло.
Т еплоемкость
газа при изотермическом процессе
еплоемкость
газа при изотермическом процессе
![]() бесконечно велика, т.к. при
бесконечно велика, т.к. при
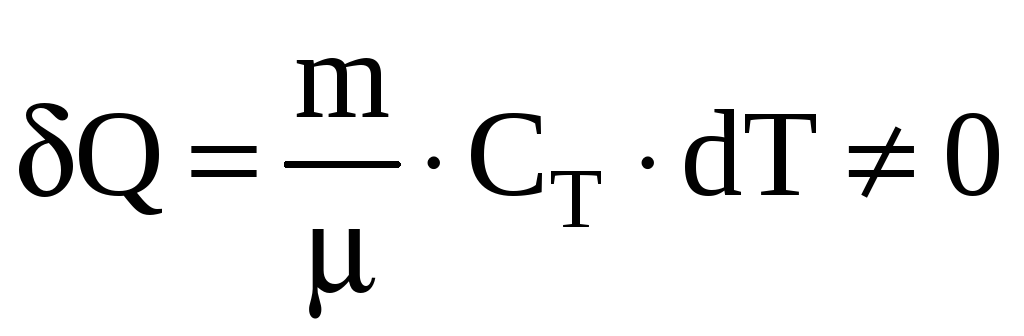 и
и
![]()
![]() может быть равно только
может быть равно только
![]() .
.
Адиабатным
называется процесс, при котором
отсутствует теплообмен между
термодинамической системой и окружающей
средой. Условие адиабатного процесса
![]() .
.
Адиабатный
процесс осуществляется при достаточно
быстром расширении или сжатии газа, так
что теплообмен между газом и окружающей
средой не успевает произойти. Из 1-го
начала термодинамики следует, что при
адиабатном процессе
![]() .
Это значит, что работа совершается
системой за счет убыли ее внутренней
энергии. В случае идеального газа,
.
Это значит, что работа совершается
системой за счет убыли ее внутренней
энергии. В случае идеального газа,
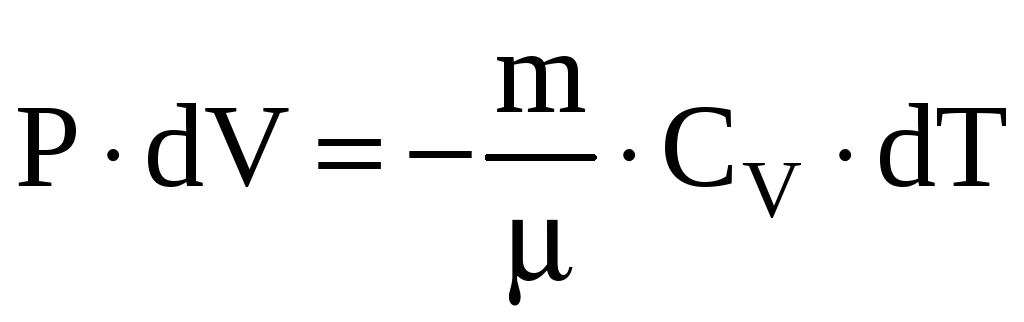 .
Отсюда видно, что при адиабатном
расширении
.
Отсюда видно, что при адиабатном
расширении
![]() ,
т.е.
,
т.е.
![]() ,
а
,
а
![]() ,
т.е. газ охлаждается. При адиабатном
сжатии
,
т.е. газ охлаждается. При адиабатном
сжатии
![]() ,
т.е.
,
т.е.
![]() ,
а
,
а
![]() ,
т.е. газ нагревается. Теплоемкость газа
при адиабатном процессе
,
т.е. газ нагревается. Теплоемкость газа
при адиабатном процессе
![]() ,
поскольку при
,
поскольку при
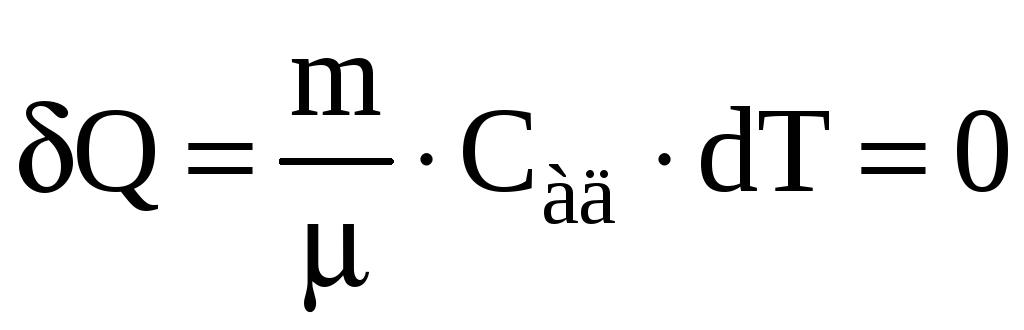 и
и
![]()
![]() .
.
Найдем
связь между параметрами идеального
газа в адиабатном процессе.
![]() ,
или
,
или
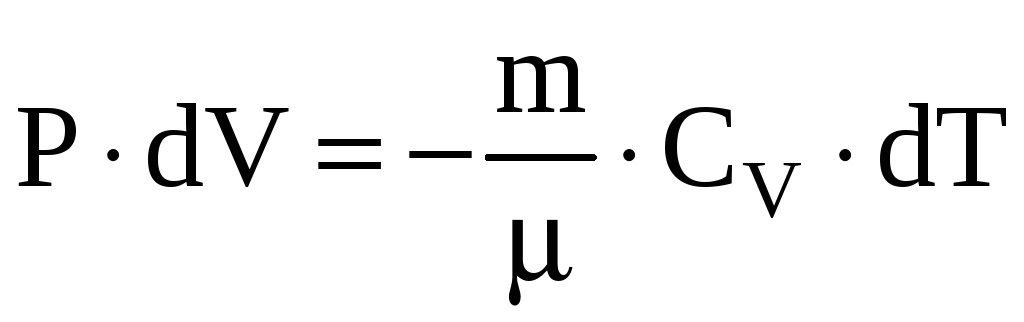 .
Из уравнения Менделеева-Клапейрона при
дифференцировании получаем
.
Из уравнения Менделеева-Клапейрона при
дифференцировании получаем
 .
Следовательно,
.
Следовательно,
![]() .
Тогда
.
Тогда
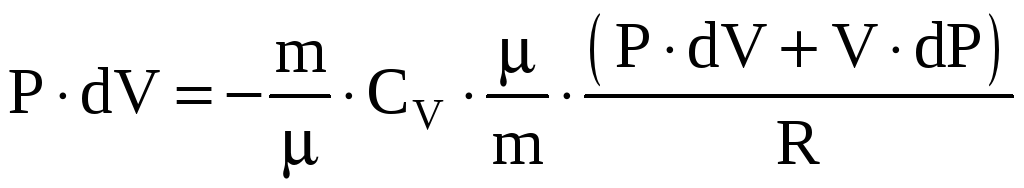 .
Или
.
Или
![]() .
С учетом уравнения Майера, получим
.
С учетом уравнения Майера, получим
![]() .
Отсюда
.
Отсюда
 .
Величину
.
Величину
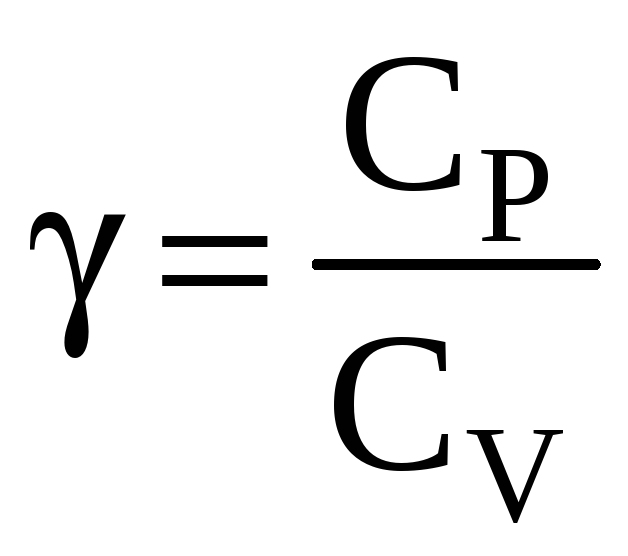 называют показателем адиабаты. Интегрируя
полученное уравнение, получаем связь
между давлением и объемом идеального
газа при адиабатном процессе
называют показателем адиабаты. Интегрируя
полученное уравнение, получаем связь
между давлением и объемом идеального
газа при адиабатном процессе
![]() .
Это уравнение Пуассона или уравнение
адиабатного процесса.
.
Это уравнение Пуассона или уравнение
адиабатного процесса.
Г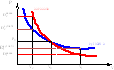 рафик
адиабатного процесса показан на рисунке.
Показатель адиабаты
рафик
адиабатного процесса показан на рисунке.
Показатель адиабаты
![]() ,
поэтому адиабата идет круче изотермы,
иначе говоря при адиабатном расширении
температура газа уменьшается,
следовательно, давление газа падает
быстрее, чем при изотермическом
расширении.
,
поэтому адиабата идет круче изотермы,
иначе говоря при адиабатном расширении
температура газа уменьшается,
следовательно, давление газа падает
быстрее, чем при изотермическом
расширении.
Воспользовавшись
уравнением Менделеева-Клапейрона
уравнение адиабатного процесса можно
выразить через другие параметры
идеального газа
![]() или
или
![]() .
.
Работа,
совершаемая идеальным газом при
адиабатном процессе может быть найдена
из условия
![]() или
или
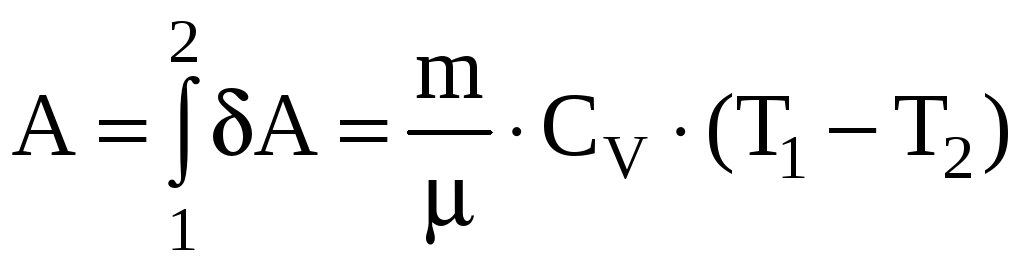 ,
или
,
или
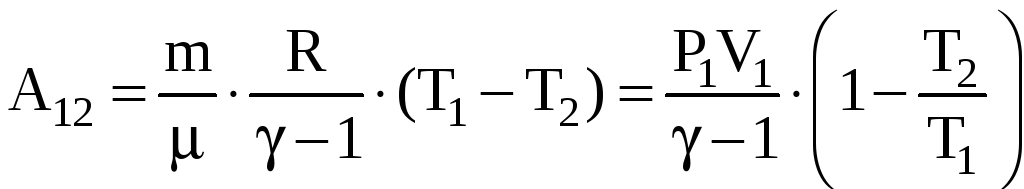 .
.
Внутренняя
энергия идеального газа складывается
из кинетической энергии его отдельных
молекул. Если молекула имеет
![]() степеней свободы, то ее средняя
кинетическая энергия
степеней свободы, то ее средняя
кинетическая энергия
![]() .
Тогда внутренняя энергия 1 моля идеального
газа
.
Тогда внутренняя энергия 1 моля идеального
газа
![]() ,
где
,
где
![]() - число Авогадро и
- число Авогадро и
![]() .
.
Молярная
теплоемкость идеального газа при
постоянном объеме
![]() ,
а при постоянном давлении
,
а при постоянном давлении
![]() .
Тогда показатель адиабаты
.
Тогда показатель адиабаты
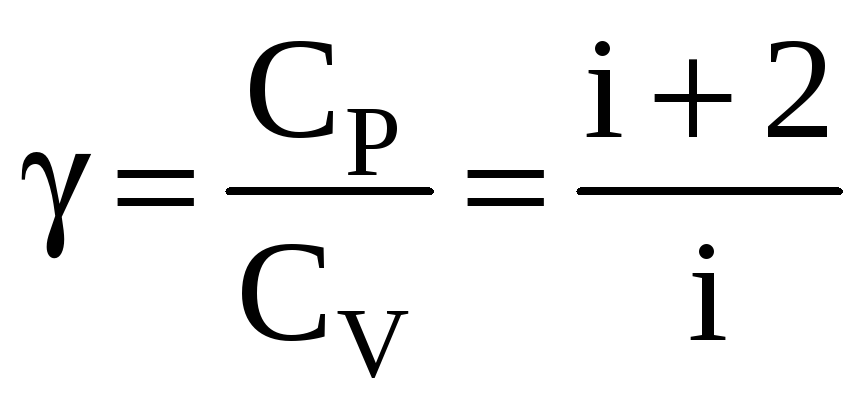 .
.
