Метод простых итераций

Метод простых итераций

Пусть известно, что корень уравнения принадлежит отрезку .

Методика решения задачи.

1. Уравнение равносильным преобразованием привести к виду . Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия ( – некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой и кривой .

2. Задать начальное приближение и малое положительное число . Положить .

3. Вычислить следующее приближение

. (1)

4. Если , итерации завершаются и .

Если , положить и перейти к п.3.

Преобразование уравнения к равносильному виду может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования .

1. Уравнение заменяется равносильным , где . Тогда, принимая правую часть этого уравнения за и раскрывая , получим условие

. (2)

Таким образом, можно найти константу на отрезке так, чтобы удовлетворялись неравенства (2). При этом надо стремиться получить такую постоянную , которая бы больше отличалась от нуля, и тогда будет реализовываться более быстрая сходимость.

2. Уравнение заменяется равносильным 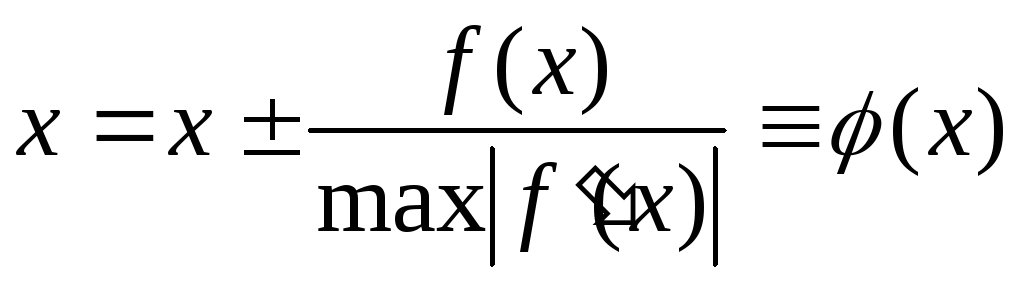, где знак в правой части выбирается из условия .

3. Из уравнения выражается так, чтобы для полученного уравнения выполнялось условие сходимости в окрестности искомого корня.

Пример 1. Найти корень уравнения методом простых итераций с точностью .

Решение.

Корень уравнения . Преобразуем уравнение к виду . Для этого запишем его сначала в форме . Функция не удовлетворяет условию сходимости, так как , , . Поэтому воспользуемся другим преобразованием.

В результате получим . Можно проверить, что на отрезке , то есть достаточное условие сходимости выполняется.

Зададим начальное приближение . Выполним расчеты по формуле (1): ,

Результаты расчетов приведены в таблице 1.

Таблица 1.

0	-1	-
1	-1,2599	0,2599
2	-1,3123	0,0524
3	-1,3223	0,0100

Таким образом, .

Пример 2. Найти корень уравнения методом простых итераций с точностью .

Решение.

Корень уравнения . Преобразуем исходное уравнение к виду : . Проверкой можно убедиться, что на отрезке , то есть достаточное условие сходимости выполняется.

В качестве начального приближения выберем .

Выполним последовательные действия по формуле (3.7): .

Результаты расчетов приведены в таблице 2.

Таблица 2.

0	0,7500	-
1	0,6873	0,0627
2	0,7091	0,0218
3	0,7015	0,0076

На третьей итерации выполнилось условие , поэтому процесс завершен. В качестве приближенного решения возьмем .