
П13_14
.pdfРЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
НГАСУ 2014 2 курс
Обыкновенные Дифференциальные Уравнения
dy |
= f (x, y ) |
y = y(x) – неизвестная функция |
|
x – независимая переменная |
|||
|
|||
dx |
f (x, y) – заданная правая часть |
||
•Уравнение задает поле направлений на плоскости (x, y).
•В каждой точке плоскости известна производная от искомой функции y(x)
•Единственное решение выделяется заданием начального условия – значения искомой функции в начальной точке: y(x0) = y0
Задача Коши для ОДУ 1 порядка |
2 |
|
Методы решения задачи Коши
•аналитические (точные)
•приближенные
Приближенные методы:
•Явные
•Неявные
•Одношаговые (м. Эйлера, Рунге-Кутта)
•Многошаговые (Адамса)
Одношаговые методы: Для нахождения решения на слое n+1 необходимо знать решение на слое n. Старт метода – с использованием начальных данных
Многошаговые методы: Для нахождения решения на
слое n+1 необходимы значения на cлоях n, n-1, n-2,…n-m.
Для старта многошагового метода необходимо сделать несколько шагов по одношаговому методу
Одношаговые методы решения ОДУ
|
|
|
|
|
dy |
= f (x, y ) |
|
y(x0) = y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Будем искать приближенное решение на отрезке [ x0, xN ] |
|
||||||||||||||||||||||||||||||||||
c шагом |
h = |
xN − x0 |
в узлах |
xi |
= |
x0 |
+ |
ih, |
( |
= |
0, 1,..., |
N |
) |
||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|
N |
|
|
|
|
|
|
i |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цель – построить |
|
|
|
|
|
x0 |
|
x1 |
|
|
|
… |
|
|
xN |
|
|
|
|
|
|
|
|
||||||||||||
таблицу |
|
|
|
|
|
|
|
|
y0 |
|
y1 |
|
|
|
… |
|
|
yN |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y(xi +1 ) − y(xi ) |
|
|
|
yi +1 − yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
dy |
|
|
|
|
|
≈ |
|
= |
|
|
|
«разность вперед» |
|||||||||||||||||||||||
dx |
|
x= x |
|
|
|
|
h |
|
|
|
h |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
yi |
+ |
− y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||
|
|
|
|
|
i |
1 |
|
|
i |
= f (x |
, y ), |
|
|
i = 0,1,..., N −1, |
|
y |
|
= y |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
h |
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Явная схема Эйлера |
4 |
|

РЕАЛИЗАЦИЯ ЯВНОГО МЕТОДА ЭЙЛЕРА
|
dy |
= f (x, y ) |
y = y0 при x = x0. |
|
|
|||||||
|
|
|
|
|||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
Явная схема Эйлера: |
|
yi +1 − yi |
= f (xi , yi ), |
|
|
|||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
y |
= y |
i |
+ h f (x , y |
), |
|
i = 0,1,..., N −1, y |
0 |
= y0 |
||||
|
i +1 |
|
|
i i |
|
|
|
|
|
|||
|
y0 − |
известно |
|
|
|
|
|
|
|
|||
y1 = y0 + h f (x0 , y0 ), |
|
|
|
Таблица |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 = y1 + h f (x1 , y1 ), |
... |
|
приближенного |
|
||||||||
|
|
|
|
|
|
|
|
|
|
решения построена |
||
yN = yN −1 + h f (xN −1 , yN −1 ), |
5 |
Пример 1
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
= |
|
3t 2 |
|
|
u(1) = 1 |
|
|
|||||||
Решить задачу Коши |
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|||
Решение ищем на отрезке [1, 2] с шагом h=0.25 |
|
||||||||||||||||||||||||||||
Сетка: t0=1, t1=1.25; t2=1.5; t3=1.75; t4=2 |
|
|
|
|
|
||||||||||||||||||||||||
Используем явный |
|
|
|
|
ui +1 |
|
= ui |
+ h |
3ti |
2 |
, i = 0, 1, 2, 3 |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
метод Эйлера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui |
|
|
|
|
|
|||||
u 0 |
= 1; |
u1 = u 0 |
+ h |
|
3t 0 |
2 |
= 1.75 ; |
|
|
|
|
|
|
||||||||||||||||
|
u 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u |
|
= u |
|
+ h |
3t1 |
2 |
|
= 2.42 ; |
|
|
|
u |
|
|
= u |
|
|
+ h |
3t 2 |
2 |
= 3.12 |
||||||||
2 |
1 |
|
|
|
|
|
|
|
3 |
2 |
u 2 |
|
|||||||||||||||||
|
|
|
|
u1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
u 4 |
= u 3 |
+ h |
3t3 |
2 |
|
= 3.85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
u 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
НЕЯВНЫЕ МЕТОДЫ
|
dy |
= f |
(x, y ) |
dy |
|
= |
|
yi − yi −1 |
Разность |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
dx |
|
|
dx |
x= x |
|
|
|
h |
«назад» |
|||
|
|
|
|
|
|
i |
|
|
|
yi − yi −1 |
= f (xi , yi ), |
||
Неявная схема Эйлера: |
|
|
|||||||||||
|
|
h |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
yi |
+ h f (xi , yi ) = yi −1 , |
|
i = 1,..., N , |
= |
0 |
||||||
|
|
|
y0 = |
yy |
|||||||||
y0 − известно
Чтобы найти y1 надо решить нелинейное уравнение
y1 + h f (x1 , y1 ) = y0 , |
|
|
Метод имеет более сложную |
|
||||||
|
|
… |
|
|
|
|
|
|
реализацию |
|
y |
N |
+ h f (x |
N |
, y |
N |
) = y |
N −1 |
, |
Используют для решения |
7 |
|
|
|
|
|
«жестких» систем ОДУ |
|||||
|
|
|
|
|
|
|
|
|
|
|

ПОРЯДОК ТОЧНОСТИ МЕТОДОВ ЭЙЛЕРА
Определяется главным членом погрешности в формуле численного дифференцирования
f+' (xi ) = fi′ |
|
+ ... |
Погрешность ~ h1 |
|
При уменьшении h в два раза погрешность уменьшится тоже в 2 раза
Более точными будут методы, в которых ошибка ~h2 , т.е. методы второго порядка,
8

Пример 1: решение в MathCAD
|
|
|
|
|
|
|
|
|
|
du |
= |
3t |
2 |
, |
u(1) = 1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решить задачу Коши dt |
|
|
|
|||||||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
|||||||||||||||
Точное решение: u(t) := |
2 t3 − 1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Проверка точного решения: |
|
|
|
|
|||||||||||||||||
|
Левая часть: |
|
|
|
|
|
|
|
|
Правая часть: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
d |
|
|
|
3 t |
2 |
|
|
|
|
|
|
|
|
|
3 t |
|
3 t |
||||||
|
u(t) → |
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
u(t) |
|
2 t3 − 1 |
||||||||
|
|
|
2 t |
3 |
− 1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Левая часть = Правая часть |
|
|
|
|
|||||||||||||||||
Начальные данные: |
|
|
|
|||||||||||||||||||||
u(1) = |
2 13 −1 = 1 |
|||||||||||||||||||||||
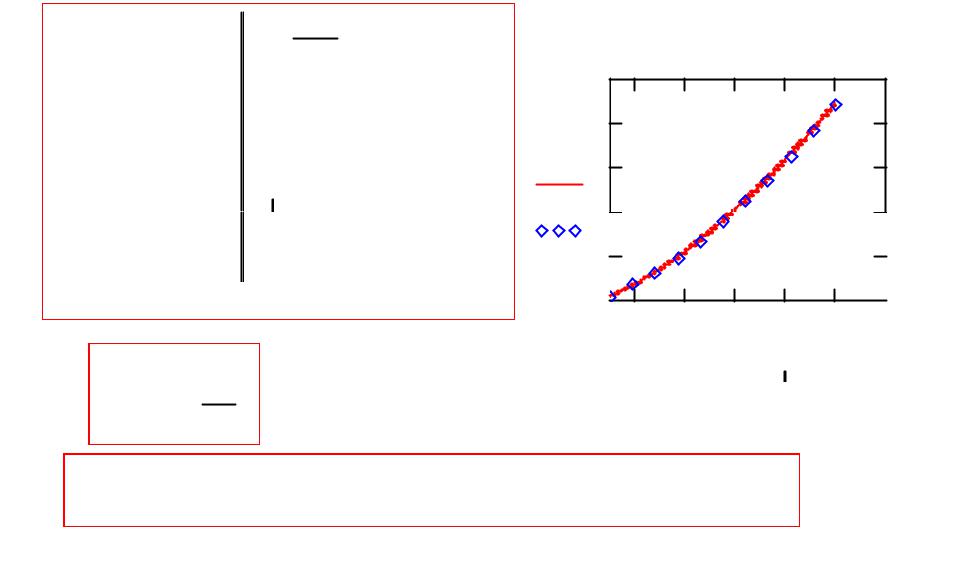
Пример 1: решение в MathCAD
|
50 |
|
|
|
|
|
|
40 |
|
|
|
|
|
u( t) |
30 |
|
|
|
|
|
y |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
4 |
6 |
8 |
10 |
12 |
3t2 |
|
|
t , x |
|
|
|
|
|
|
|
|
|
|
f(t , y) := |
|
|
|
|
|
|
y
x := euler(1, 10, 10, 1, f) 0 |
y := euler(1, 10, 10, 1, f) 1 |
