
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ЗАДАЧИ СТАТИКИ ТВЕРДОГО ТЕЛА
- •1.1. Сила – основное понятие статики
- •1.2. Аксиомы статики
- •1.3. Теорема о равновесии трех сил
- •1.4. Проекция силы на ось и плоскость
- •2. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- •2. 1. Свободное и несвободное тело. Активные и реактивные силы
- •2. 2. Основные типы связей
- •3. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- •3. 1. Графический и аналитический методы определения равнодействующей сходящихся сил
- •3. 2. Условие и уравнения равновесия системы сходящихся сил
- •3. 3. Примеры решения задач на систему сходящихся сил
- •4. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
- •4. 1. Момент силы относительно точки на плоскости
- •4. 2. Момент силы относительно точки в пространстве
- •5. ТЕОРИЯ ПАР СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- •5. 1. Пара сил. Момент пары сил на плоскости
- •5. 2. Момент пары сил в пространстве. Эквивалентные пары
- •5. 3. Теоремы об эквивалентности пар
- •5.4. Сложение пар сил на плоскости
- •5. 5. Сложение пар сил в пространстве
- •5. 6. Условия равновесия системы пар сил
- •6. ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
- •6. 1. Приведение силы к заданному центру
- •6. 2. Приведение плоской системы сил к заданному центру
- •6. 3. Частные случаи приведения плоской системы сил к заданному центру
- •6. 4. Уравнения равновесия плоской произвольной системы сил
- •6. 5. Уравнения равновесия плоской системы параллельных сил
- •6.6. Теорема Вариньона о моменте равнодействующей плоской системы сил
- •6. 7. Статически определимые и статически неопределимые задачи
- •6. 8. Примеры решения задач на равновесие плоской произвольно расположенной системы сил
- •7. РАВНОВЕСИЕ СОСТАВНЫХ СИСТЕМ
- •7. 1. Аналитические условия равновесия составных систем
- •7.2. Графические условия равновесия простых и составных систем
- •8. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ
- •8. 1. Основные понятия о ферме и усилиях в ее стержнях
- •8.2. Условие геометрической неизменяемости и статической определимости фермы
- •8.3. Методы расчета фермы
- •8.3.1. Метод вырезания узлов
- •8.3.2. Леммы о нулевых стержнях фермы
- •8.3.3. Метод сечений (метод Риттера)
- •9. РАВНОВЕСИЕ ТЕЛА ПРИ НАЛИЧИИ ТРЕНИЯ
- •9.1. Трение скольжения и его законы
- •9.2. Конус трения
- •9.4. Трение качения
- •10. ПРОСТРАНСТВЕННАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
- •10.1. Момент силы и главный момент системы сил относительно оси
- •10.2. Зависимость между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку
- •10.3. Аналитические выражения моментов силы относительно координатных осей
- •10.4. Приведение пространственной системы сил к данному центру
- •10.5. Возможные случаи приведения пространственной системы сил к данному центру
- •10.7. Выражения главного вектора и главного момента пространственной системы сил через их проекции на оси координат
- •10.8. Уравнения равновесия пространственной системы сил
- •10.9. Теорема Вариньона о моменте равнодействующей пространственной системы сил
- •10.10. Примеры решения задач на приведение пространственной системы сил к простейшему виду
- •10.11. Примеры решения задач на условия равновесия пространственной системы сил
- •11. ЦЕНТР ПРОСТРАНСТВЕННОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- •11. 1. Сложение системы параллельных сил. Центр параллельных сил
- •11.2. Центр тяжести твердого тела и координаты центра тяжести
- •11.3. Способы определения координат центров тяжести тел
- •11.4. Координаты центров тяжести основных площадей и линий
- •11.5. Примеры решения задач на определение координат центров тяжести сложных плоских фигур
142
Выделим сектор с центральным углом dφ, с дугой длиной dℓ = R . dφ, площадью dF = ½ R . d = ½ R . R . dφ и координатой центра тяжести х = 2/3 R Cos φ. Выразим площадь сектора ОАВ:
+α
F = ∫dF = ∫½ R2 dφ = α R2
F-α
икоординату центра тяжести
+α
Хс = ∫2/3 R Cos φ . 1/2R2 dφ / α R2 = 2/3 R . Sin α/α.
-α
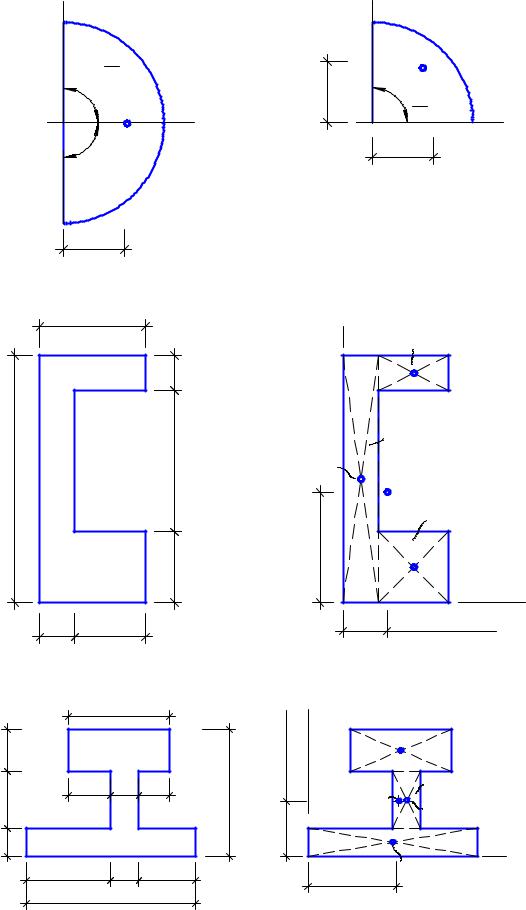
В частном случае координата центра тяжести площади полукруга Хс (рис. 11.6, а) при α = π/2 будет Хс = 4/3π . R 0,424R. Координаты центра тяжести площади четверти круга (рис. 11.6, б) при α = π/4 будут Хс = Ус = 4/3π . R.
11.5. Примеры решения задач на определение координат центров тяжести сложных плоских фигур
Пример 11. 1
Определить координаты центра тяжести плоской фигуры (рис. 11. 7, а), где размеры показаны в сантиметрах.
Решение:
1.Разделяем сложную фигуру на более простые части в виде прямоугольников (рис. 11. 7, б) с площадями F1 = 20 . 10 = 200 см2; F2 = 10 . 70 =
=700 см2; F3 = 20 . 20 = 400 см2 и общей площадью F = F1 + F2 + F3 = 1300см2.
2.Определяем координаты центров тяжести С1, С2, С3 площадей F1 , F2 , F3 относительно осей произвольно выбранной прямоугольной системы
координат хоу.
Х1 = 10 + ½ . 20 = 20 см ; Х2 = ½ . 10 = 5 см ;
Х3 = 10 + ½ . 20 = 20 см ; У1 = 60 + ½ . 10 = 65 см ; У2 = ½ . 70 = 35 см ;
У3 = ½ . 20 = 10 см .
3. Определяем координаты центра тяжести всей плоской фигуры (11. 8)
Хс = |
F 1 Х 1 + F 2 Х 2 + F 3 Х 3 |
200 . 20 + 700 . 5 + 400 . 20 |
----------------------------- = |
-------------------------------------- = 11,92 см |
|
|
F |
1300 |
Ус = |
F 1 У 1 + F 2 У 2 + F 3 У 3 |
200 . 15 + 700 . 35 + 400 . 10 |
= -------------------------------------- |
= 31,92 см |
|
|
F |
1300 |
|
|
|
|
|
143 |
|
|
|
|
|
|
a. |
y |
|
|
|
|
б. |
y |
|
|
|
|
|
R |
a= p |
|
|
|
R |
|
|
|
|
|
|
|
2 |
|
|
|
Yc |
|
|
|
С |
|
|
|
|
|
x |
|
|
|
|
p |
x |
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
0 |
|
|
2 |
||
|
a |
|
С |
|
|
Xc |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.6 |
|
|
|
|
|
|
a. |
|
3,00 |
|
|
б. |
y |
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,00 |
|
|
|
|
|
С1 |
|
|
|
|
|
4,00 |
|
|
|
F2 |
|
|
|
7,00 |
|
|
|
|
С2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
||
|
|
|
|
|
|
см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F3 |
|
|
|
|
|
|
|
|
Yc = 31,92 |
|
|
|
|
|
|
|
|
|
2,00 |
|
|
|
|
С3 |
x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1,00 |
2,00 |
|
|
0 |
|
|
Xc = 11,92 см |
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Рис. 11.7 |
|
|
|
|
|
|
|
a. |
36 |
|
б. |
y |
|
|
|
|
|
|
|
|
|
|
|
см |
|
|
|
С1 |
|
|
15 |
|
|
|
|
20,34 |
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
15 |
10 |
11 |
Yс = |
|
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
||||
20 |
|
|
|
45 |
|
|
|
С |
|
С2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
F3 |
x |
|
30 |
|
10 |
20 |
|
Xc = 31,96 см |
С3 |
|
|
||
|
|
60 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.8 |
|
|
|
|
|
|
144
Пример 11. 2
Определить координаты центра тяжести плоской фигуры (рис. 11. 8, а) с размерами в сантиметрах.
Решение:
1.Разделяем сложную фигуру на более простые части в виде прямоугольников (рис. 11. 8, б) с площадями F1 = 36 . 15 = 540 см2; F2 = 10 . 20 =
=200 см2; F3 = 60 . 10 = 600 см2 и общей площадью F = F1 + F2 + F3 = 1340см2.
2.Определяем координаты центров тяжести С1, С2, С3 площадей F1 , F2 , F3 относительно осей произвольно выбранной прямоугольной системы координат хоу.
Х1 = 30 - 15 + 36 / 2 = 33 см ; Х2 = 30 + 5 = 35 см ; Х3 = 60 / 2 = 30 см ;
У1 = 10 + 20 + 15 / 2 = 37,5 см ; У2 = 10 + 20 / 2 = 20 см ;
У3 = 10 / 2 = 5 см .
3. Определяем координаты центра тяжести всей плоской фигуры (11. 8)
F1 |
Х1 |
+ F2 |
Х2 |
+ F3 Х3 |
540 . 33 + 200 . 35 + 600 . 30 |
Хс = ----------------------------- |
|
F |
|
= |
-------------------------------------- = 31,96 см |
|
|
|
|
1340 |
|
F1 |
У1 |
+ F2 |
У2 |
+ F3 У3 |
540 . 37,5 + 200 . 20 + 600 . 5 |
Ус = ----------------------------- |
|
F |
|
= -------------------------------------- |
= 20,34 см |
|
|
|
|
1340 |
Пример 11. 3
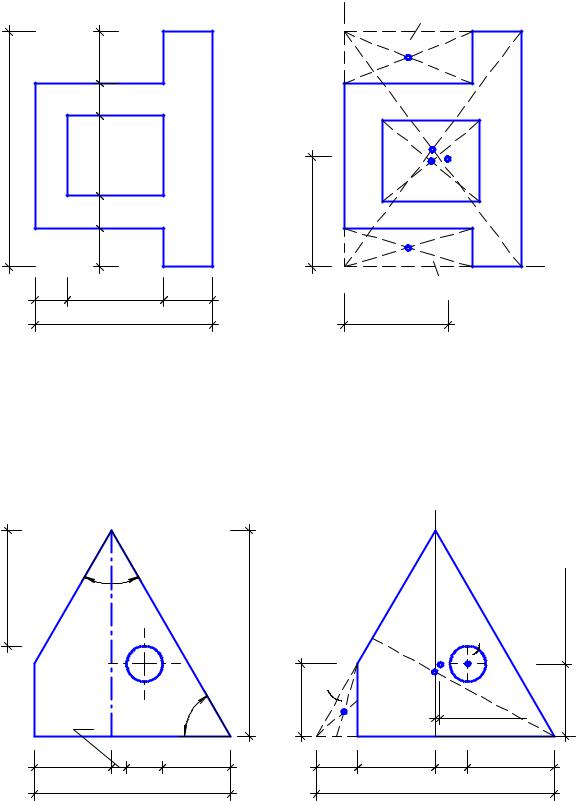
Определить координаты центра тяжести плоской фигуры (рис. 11. 9, а) с размерами в сантиметрах.
Решение:
1. Разделяем сложную фигуру на более простые части в виде
прямоугольников (рис. 11. 9, б) с площадями F1 = 55 . 73 = 4015 см2; F2 = - (5515) . 12 = - 480 см2; F3 = - 30 . 25 = - 750 см2 ; F4 = - (55 - 15) . 16 = - 640 см2 и
общей площадью F = F1 + F2 + F3 + F4 = 4015 - 480 - 750 - 640 = 2145 см2.
2. Определим координаты центров тяжести С1, С2, С3, С4 площадей F1 , F2 , F3, F4 относительно осей произвольно выбранной прямоугольной системы координат хоу.
Х1 = 55 / 2 = 27,5 см ; Х2 = (55 – 15) / 2 = 20 см ; Х3 = 10 + 30 / 2 = 25 см ; Х4 = (55 – 15) / 2 = 20 см ; У1 = 73 / 2 = 36,5 см ; У2 = 12 / 2 = 6 см ;
У3 = 12 + 10 + 25 / 2 = 34,5 см .
У4 = 12 + 10 + 25 +10 + 16 / 2 = 65 см .
а. |
|
|
|
16 |
|
|
10 |
|
73 |
25 |
|
|
10 |
|
|
12 |
|
10 |
30 |
15 |
|
55 |
|
145
б. |
y |
F4 |
|
|
|
|
|
С4 |
|
|
F1 |
|
С1 |
F3 |
С |
cм |
С3 |
35,52 |
|
Yc = |
|
С2 |
|
0 |
F2 |
Yc = 32,29 cм
Рис. 11.9
x
39,03
18,25 12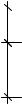
а.
60Е
69,28
5 |
|
6 |
0 |
Е |
|
|
|
||
26 |
12 |
|
|
23 |
|
66 |
|
|
|
24,25
б. y
|
|
F1 |
|
|
|
|
С |
F3 |
|
|
|
С3 |
||
F2 |
|
С1 |
||
|
|
|||
|
С2 |
Xc = 1,59 см |
||
|
0 |
|
||
14 |
26 |
29 |
||
11 |
||||
|
|
80 |
|
|
Yc = 24,06 см
x
Рис. 11.10
146
3. Определяем координаты центра тяжести всей фигуры (11. 8)
|
4 |
|
|
∑ F i . Х i |
4015 . 27,5 - 480 . 20 - 750 . 25 – 640 . 20 |
|
i=1 |
|
Хс = |
------------- = |
------------------------------------------------------ = 32,29 см |
|
F |
2145 |
|
4 |
|
|
∑ F i . У i |
4015 . 36,5 - 480 . 6 - 750 . 34,5 – 640 . 65 |
|
i=1 |
|
Ус = ------------- |
= ------------------------------------------------------ |
= 35,52 см |
|
F |
2145 |
Пример 11. 4
Определить координаты центра тяжести плоской фигуры (рис. 11. 10, а) в виде равностороннего треугольника с вырезами и размерами в сантиметрах.
Решение:
1. Разделяем сложную фигуру на простые части в виде равностороннего треугольника с положительным значением площади F1 (рис. 11.10, б), прямоугольного треугольника с отрицательной площадью F2 кругового выреза с отрицательной площадью F3, то есть
F1 = ½ 80 . 69,28 = 2771,2 см2 ;
F2 = -½ 14 . 24,25 = - 169,75 см2 ;
F3 = - π . 62 = - 113,09 см2 ;
иобщей площадью F = F1 + F2 + F3 = 2771,2 – 169,75 – 113,09 = 2488,36см2.
2.Определим координаты центров тяжести С1, С2, С3 площадей F1 , F2 , F3 относительно осей произвольно выбранной прямоугольной системы координат хоу:
Х1 = 0 ; У1 = 1/3 . 40 . tg60° = 23,09 см ;
Х2 = - (40 – 2/3 . 14) = - 30,67 см ; У2 = 1/3 . 14 . tg60° = 8,08 см ; Х3 = 5 + 6 = 11 см ;У3 = 14 . tg60° = 24,25 см .
3. Определяем координаты центра тяжести всей плоской фигуры (11. 8)
F1 Х1 |
+ F2 Х2 + F3 Х3 |
2771,2 . 0 – 169,75 . (-30,67) – 113,09 . 11 |
|
Хс = ----------------------------- |
F |
= ---------------------------------------------------- |
= 1,59 см |
|
2488,36 |
|
|
F1У1 |
+ F2У2 + F3У3 |
2771,2 . 23,09–169,75 . 8,08-113,09 . 24,25 |
|
Ус = --------------------------- |
= |
-----------------------------------------------------2488,36 |
= 24,06 см |
|
F |
|
147
Пример 11. 5
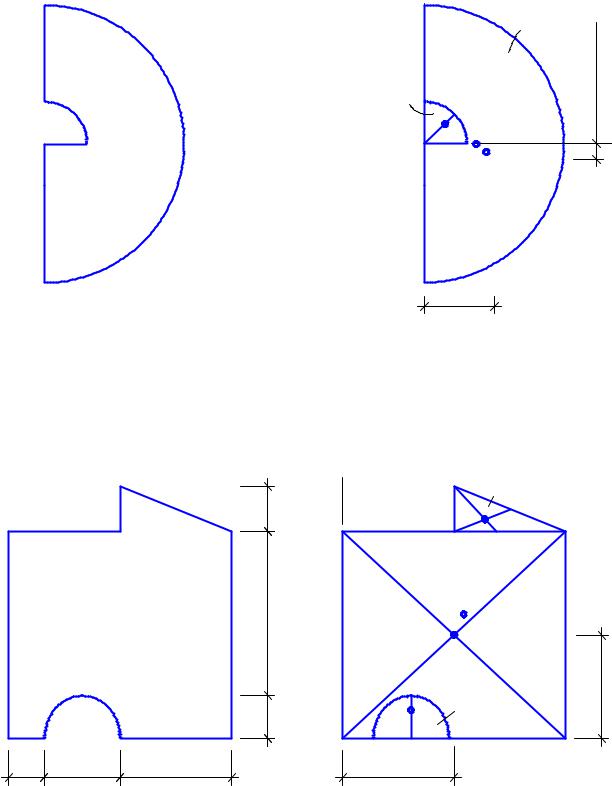
Определить координаты центра тяжести полукруга радиусом R = 60 см с вырезом – сегментом радиусом r = 15 см (рис. 11. 11, а).
Решение:
1. Разделяем сложную фигуру на две простейшие в виде полукруга,
сегмента с площадями
F1 = ½ πR2 = ½ π . 602 = 5654,7 см2 ; F2 = -1/4 πr2 = -1/4 π . 152 = - 176,71 см2 ;
и общей площадью
F = F1 + F2 = 5654,7 – 176,71 = 5478 см2.
2. Определяем координаты центров тяжести С1, С2 площадей F1 , F2 относительно осей произвольно выбранной прямоугольной системы координат хоу:
|
Х1 = 4/3π . R = 4/3π . 60 = 25,47 см ; У1 = 0 ; |
||
|
Х2 = 4/3π . r = 4/3π . 15 |
= 6,37 см ; У2 = Х2 = 6,37 см. |
|
3. Определяем координаты центра тяжести всей фигуры (11. 8) |
|||
F1 Х1 + F2 Х2 |
5654,7 |
. 25,47 – 176,71 . 6,37 |
|
Хс = ------------------- |
= ---------------------------------------- |
|
= 26,09 см |
|
F |
|
5478 |
Ус = |
F1У1 + F2У2 |
5654,7 . 0 – 176,71 . 6,37 |
|
= ----------------------------------- |
|
= - 0,21 см |
|
|
F |
|
5478 |
Пример 11. 6
Определить координаты центра тяжести плоской фигуры (рис. 11. 12, а) с размерами в сантиметрах.
Решение:
1. Разделяем сложную фигуру на простые части в виде прямоугольного треугольника площадью F1 , прямоугольника площадью F2 , полукруга с
отрицательной площадью F3 , то есть F1 = ½ 9 . 3 = 13,5 см2; F2 = 18 . 15 = 270
см2; F3 = -1/2 π . 32 = - 14,14 см2 и общей площадью F = F1 + F2 + F3 = 13,5 + 270 - 14,14 = 269,36 см2.
2. Определяем координаты центров тяжести С1, С2, С3 площадей F1 , F2 , F3 относительно осей произвольно выбранной прямоугольной системы
координат хоу (рис. 11. 12, б):
Х1 = 9 + 1/3 . 9 = 12 см ;
Х2 = 9 см ;
Х3 = 3 + 3 = 6 см ; У1 = 15 + 1/3 . 3 = 16 см ;
У2 = 15/2 = 7,5 см ; У3 = 4/3π . 3 = 1,272 см .
3. Определяем координаты центра тяжести всей плоской фигуры (11. 8)
Хс = |
F1 Х1 + F2 Х2 + F3 Х3 |
13,5 . 12 + 270 . 9 – 14,14 . 6 |
----------------------------- = -------------------------------------- |
= 9,308 см |
|
|
F |
269,36 |
|
148 |
|
|
а.. |
б. |
|
y |
|
|||
|
|
||
|
|
|
|
F1
|
F2 |
|
r=15 cм |
o С2 С1 |
|
С |
||
|
||
R=60 cм |
|
Xc = 26,09 cм
Рис. 11.11
Yc = - 0,21 cм
x
а..
3 см
3 см 12 см
3 см |
6 см |
9 см |
y |
б. |
F |
|
|
1 |
|
|
С1 |
С
F2 С2
С3 F3
о
Xc = 9,308 см
Yc = 8,253 см
x
Рис. 11.12
149
Ус = |
F1 У1 + F2 У2 + F3 У3 |
13,5 . 16 + 270 . 7,5 – 14,14 . 1,272 |
----------------------------- = |
-------------------------------------------- = 8,253 см |
|
|
F |
269,36 |
Пример 11. 7
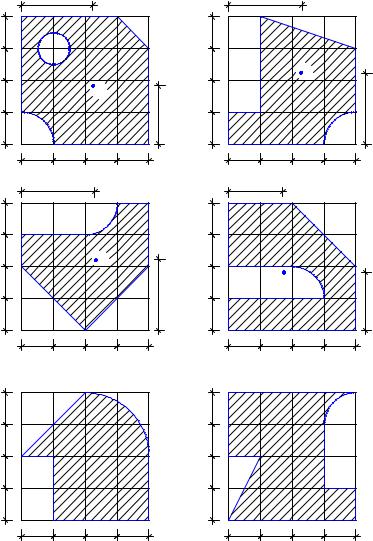
Определить координаты центра тяжести плоских фигур (рис. 11. 13) с размерами в сантиметрах.
Результаты решения:
Рис. 11. 13, а. ХС = 7,51 см ; УС = 7,10 см ; Рис. 11. 13, б. ХС = 9,09 см ; УС = 7,32 см ; Рис. 11. 13, в. ХС = 5,23 см ; УС = 5,09 см . Рис. 11. 13, г. ХС = 9,75 см ; УС = 9,65 см .
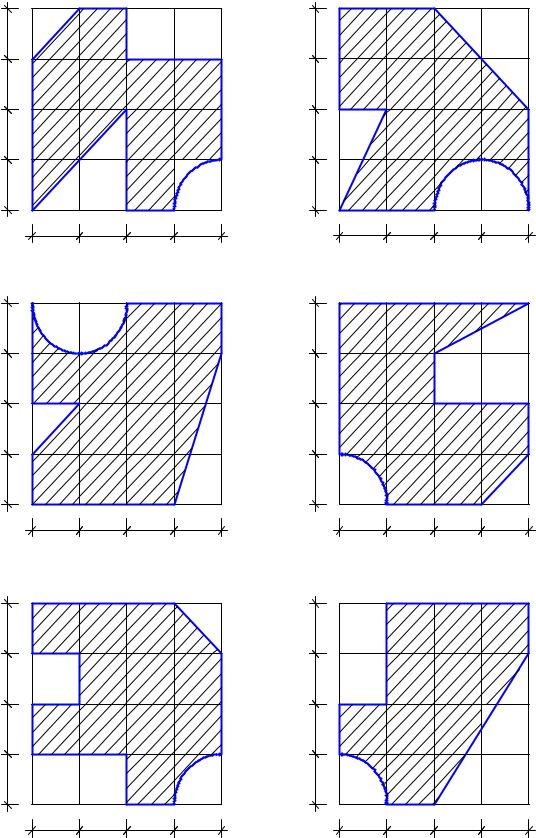
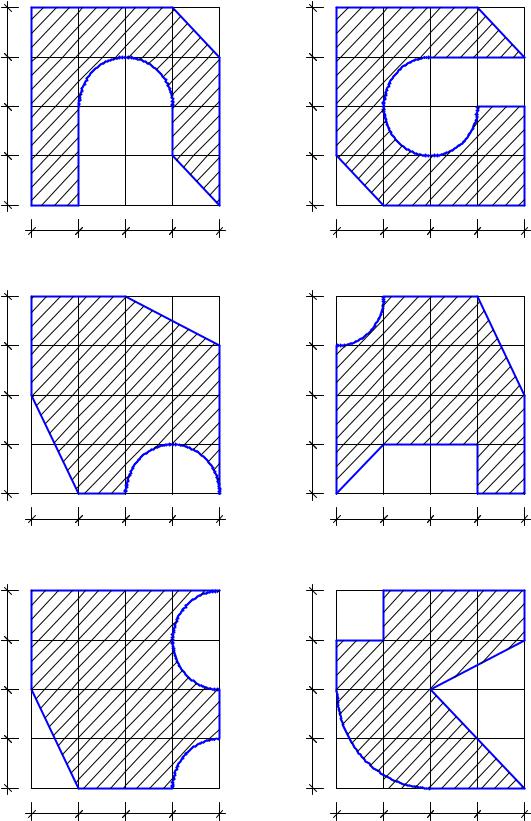
Пример 11. 8
Определить координаты центра тяжести плоских фигур (рис. 11. 13, д, е рис. 11.14, рис. 11.15) с размерами в сантиметрах самостоятельно.
а |
Xc |
|
б |
3,6 |
|
|
4,2 |
3,6 |
|
|
4,2 |
3,6 |
|
С |
4,2 |
|
|
||
3,6 |
|
|
Yc |
|
|
4,2 |
|
3,6 |
3,6 |
3,6 |
3,6 |
в |
Xc |
|
г |
2,4 |
|
|
5,1 |
2,4 |
|
С |
5,1 |
|
|
|
|
2,4 |
|
|
5,1 |
|
|
|
Yc |
2,4 |
|
|
5,1 |
2,4 |
2,4 |
2,4 |
2,4 |
д |
|
|
е |
4,0 |
|
|
3,0 |
4,0 |
|
|
3,0 |
4,0 |
|
|
3,0 |
4,0 |
|
|
3,0 |
4,0 |
4,0 |
4,0 |
4,0 |
|
|
|
Рис. 11.13 |
|
Xc |
|
|
|
|
С |
|
|
|
|
Yc |
4,2 |
4,2 |
4,2 |
4,2 |
|
Xc |
|
|
|
С |
|
|
|
|
|
Yc |
5,1 |
5,1 |
5,1 |
5,1 |
3,0 |
3,0 |
3,0 |
3,0 |
3,4 |
|
|
|
3,4 |
|
|
|
3,4 |
|
|
|
3,4 |
|
|
|
3,4 |
3,4 |
3,4 |
3,4 |
5,0 |
|
|
|
5,0 |
|
|
|
5,0 |
|
|
|
5,0 |
|
|
|
5,0 |
5,0 |
5,0 |
5,0 |
6,0 |
|
|
|
6,0 |
|
|
|
6,0 |
|
|
|
6,0 |
|
|
|
6,0 |
6,0 |
6,0 |
6,0 |
150
3,0 |
|
|
|
3,0 |
|
|
|
3,0 |
|
|
|
3,0 |
|
|
|
3,0 |
3,0 |
3,0 |
3,0 |
5,2 |
|
|
|
5,2 |
|
|
|
5,2 |
|
|
|
5,2 |
|
|
|
5,2 |
5,2 |
5,2 |
5,2 |
6,3 |
|
|
|
6,3 |
|
|
|
6,3 |
|
|
|
6,3 |
|
|
|
6,3 |
6,3 |
6,3 |
6,3 |
Рис. 11.4 |
|
|
|
151
5,4 |
|
|
|
5,4 |
|
|
|
5,4 |
|
|
|
5,4 |
|
|
|
5,4 |
5,4 |
5,4 |
5,4 |
7,2 |
|
|
|
7,2 |
|
|
|
7,2 |
|
|
|
7,2 |
|
|
|
7,2 |
7,2 |
7,2 |
7,2 |
7,4 |
|
|
|
7,4 |
|
|
|
7,4 |
|
|
|
7,4 |
|
|
|
7,4 |
7,4 |
7,4 |
7,4 |
6,9 |
|
|
|
6,9 |
|
|
|
6,9 |
|
|
|
6,9 |
|
|
|
6,9 |
6,9 |
6,9 |
6,9 |
7,6 |
|
|
|
7,6 |
|
|
|
7,6 |
|
|
|
7,6 |
|
|
|
7,6 |
7,6 |
7,6 |
7,6 |
8,2 |
|
|
|
8,2 |
|
|
|
8,2 |
|
|
|
8,2 |
|
|
|
8,2 |
8,2 |
8,2 |
8,2 |
Рис. 11.15
152
Список литературы
1.Антонов, Е.Е. Теоретическая механика / Е.Е. Антонов, Г.В. Аржаева, В.В. Родионов. – Н. Новгород, 1998. – 91 с.
2.Мещерский, И.В. Сборник задач по теоретической механике / И.В. Мещерский. – М.: Наука, 1986. – 448 с.
3.Тарг, С.М. Краткий курс теоретической механики / С.М. Тарг. – М.:
Наука, 1995. – 478 с.
4.Яблонский, А.А. Курс теоретической механики. ч.I / А.А. Яблонский, В.Н. Никифорова.– М.: Высшая школа, 1984. – 360 с.
153
|
Содержание |
|
ВВЕДЕНИЕ.................................................................................................................. |
3 |
|
1. |
ОСНОВНЫЕ ЗАДАЧИ СТАТИКИ ТВЕРДОГО ТЕЛА...................................... |
4 |
1.1. Сила – основное понятие статики....................................................................... |
5 |
|
1.2. Аксиомы статики.................................................................................................. |
7 |
|
1.3. Теорема о равновесии трех сил......................................................................... |
10 |
|
1.4. Проекция силы на ось и плоскость................................................................... |
10 |
|
2. |
СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ............................................................................ |
13 |
2.1. Свободное и несвободное тело. Активные и реактивные силы.................... |
13 |
|
2.2. Основные типы связей....................................................................................... |
13 |
|
3. |
СИСТЕМА СХОДЯЩИХСЯ СИЛ...................................................................... |
17 |
3. |
1. Графический и аналитический методы определения равнодействующей |
|
сходящихся сил.......................................................................................................... |
17 |
|
3. |
2. Условие и уравнения равновесия системы сходящихся сил........................ |
19 |
3. |
3. Примеры решения задач на систему сходящихся сил................................... |
20 |
4. |
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ .................................................. |
25 |
4.1. Момент силы относительно точки на плоскости............................................ |
25 |
|
4.2. Момент силы относительно точки в пространстве......................................... |
29 |
|
5. |
ТЕОРИЯ ПАР СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ ...................... |
30 |
5.1. Пара сил. Момент пары сил на плоскости....................................................... |
30 |
|
5.2. Момент пары сил в пространстве. Эквивалентные пары............................... |
31 |
|
5.3. Теоремы об эквивалентности пар..................................................................... |
31 |
|
5.4. Сложение пар сил на плоскости ....................................................................... |
36 |
|
5.5. Сложение пар сил в пространстве.................................................................... |
39 |
|
5.6. Условия равновесия системы пар сил.............................................................. |
39 |
|
6. |
ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ........... |
43 |
6.1. Приведение силы к заданному центру............................................................. |
43 |
|
6.2. Приведение плоской системы сил к заданному центру................................. |
45 |
|
6.3. Частные случаи приведения плоской системы сил к заданному центру..... |
46 |
|
6.4. Уравнения равновесия плоской произвольной системы сил......................... |
47 |
|
6.5. Уравнения равновесия плоской системы параллельных сил ........................ |
49 |
|
6.6. Теорема Вариньона о моменте равнодействующей плоской системы сил.. |
50 |
|
6.7. Статически определимые и статически неопределимые задачи................... |
50 |
|
6.8. Примеры решения задач на равновесие плоской произвольно |
|
|
расположенной системы сил.................................................................................... |
53 |
|
7. |
РАВНОВЕСИЕ СОСТАВНЫХ СИСТЕМ.......................................................... |
60 |
7.1. Аналитические условия равновесия составных систем................................. |
60 |
|
7.2. Графические условия равновесия простых и составных систем .................. |
69 |
|
8. |
СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ....................................................... |
76 |
8.1. Основные понятия о ферме и усилиях в ее стержнях.................................... |
76 |
|
8.2. Условие геометрической неизменяемости и статической определимости |
|
|
фермы.......................................................................................................................... |
77 |
|
8.3. Методы расчета фермы...................................................................................... |
79 |
|
154 |
|
8.3.1. Метод вырезания узлов................................................................................... |
79 |
8.3.2. Леммы о нулевых стержнях фермы .............................................................. |
81 |
8.3.3. Метод сечений (метод Риттера)..................................................................... |
82 |
9. РАВНОВЕСИЕ ТЕЛА ПРИ НАЛИЧИИ ТРЕНИЯ............................................ |
85 |
9.1. Трение скольжения и его законы...................................................................... |
86 |
9.2. Конус трения....................................................................................................... |
89 |
9.3. Примеры на равновесие сил, приложенных к твердому телу при |
|
наличии трения.......................................................................................................... |
90 |
9.4. Трение качения................................................................................................... |
96 |
10. ПРОСТРАНСТВЕННАЯ СИСТЕМА ПРОИЗВОЛЬНО |
|
РАСПОЛОЖЕННЫХ СИЛ...................................................................................... |
96 |
10.1. Момент силы и главный момент системы сил относительно оси .............. |
96 |
10.2. Зависимость между моментом силы относительно точки и моментом силы
относительно оси, проходящей через эту точку.................................................. |
100 |
10.3. Аналитические выражения моментов силы относительно |
100 |
координатных осей.................................................................................................. |
|
10.4. Приведение пространственной системы сил к данному центру............... |
101 |
10.5. Возможные случаи приведения пространственной системы сил |
103 |
к данному центру..................................................................................................... |
|
10.6. Зависимость между главным моментом пространственной системы сил |
|
относительно данного центра и главным моментом сил относительно оси, |
106 |
проходящей через этот центр................................................................................. |
|
10.7. Выражения главного вектора и главного момента пространственной |
|
системы сил через их проекции на оси координат.............................................. |
106 |
10.8. Уравнения равновесия пространственной системы сил............................ |
107 |
10.9. Теорема Вариньона о моменте равнодействующей пространственной |
|
системы сил.............................................................................................................. |
110 |
10.10. Примеры решения задач на приведение пространственной |
111 |
системы сил к простейшему виду.......................................................................... |
|
10.11. Примеры решения задач на условия равновесия пространственной |
|
системы сил.............................................................................................................. |
119 |
11. ЦЕНТР ПРОСТРАНСТВЕННОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ |
|
И ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА............................................................. |
129 |
11. 1. Сложение системы параллельных сил. Центр параллельных сил........... |
129 |
11.2. Центр тяжести твердого тела и координаты центра тяжести.................... |
132 |
11.3. Способы определения координат центров тяжести тел............................. |
135 |
11.4. Координаты центров тяжести основных площадей и линий..................... |
137 |
11.5. Примеры решения задач на определение координат центров тяжести |
142 |
сложных плоских фигур......................................................................................... |
|
Список литературы ................................................................................................ |
152 |
