
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ЗАДАЧИ СТАТИКИ ТВЕРДОГО ТЕЛА
- •1.1. Сила – основное понятие статики
- •1.2. Аксиомы статики
- •1.3. Теорема о равновесии трех сил
- •1.4. Проекция силы на ось и плоскость
- •2. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- •2. 1. Свободное и несвободное тело. Активные и реактивные силы
- •2. 2. Основные типы связей
- •3. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- •3. 1. Графический и аналитический методы определения равнодействующей сходящихся сил
- •3. 2. Условие и уравнения равновесия системы сходящихся сил
- •3. 3. Примеры решения задач на систему сходящихся сил
- •4. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
- •4. 1. Момент силы относительно точки на плоскости
- •4. 2. Момент силы относительно точки в пространстве
- •5. ТЕОРИЯ ПАР СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- •5. 1. Пара сил. Момент пары сил на плоскости
- •5. 2. Момент пары сил в пространстве. Эквивалентные пары
- •5. 3. Теоремы об эквивалентности пар
- •5.4. Сложение пар сил на плоскости
- •5. 5. Сложение пар сил в пространстве
- •5. 6. Условия равновесия системы пар сил
- •6. ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
- •6. 1. Приведение силы к заданному центру
- •6. 2. Приведение плоской системы сил к заданному центру
- •6. 3. Частные случаи приведения плоской системы сил к заданному центру
- •6. 4. Уравнения равновесия плоской произвольной системы сил
- •6. 5. Уравнения равновесия плоской системы параллельных сил
- •6.6. Теорема Вариньона о моменте равнодействующей плоской системы сил
- •6. 7. Статически определимые и статически неопределимые задачи
- •6. 8. Примеры решения задач на равновесие плоской произвольно расположенной системы сил
- •7. РАВНОВЕСИЕ СОСТАВНЫХ СИСТЕМ
- •7. 1. Аналитические условия равновесия составных систем
- •7.2. Графические условия равновесия простых и составных систем
- •8. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ
- •8. 1. Основные понятия о ферме и усилиях в ее стержнях
- •8.2. Условие геометрической неизменяемости и статической определимости фермы
- •8.3. Методы расчета фермы
- •8.3.1. Метод вырезания узлов
- •8.3.2. Леммы о нулевых стержнях фермы
- •8.3.3. Метод сечений (метод Риттера)
- •9. РАВНОВЕСИЕ ТЕЛА ПРИ НАЛИЧИИ ТРЕНИЯ
- •9.1. Трение скольжения и его законы
- •9.2. Конус трения
- •9.4. Трение качения
- •10. ПРОСТРАНСТВЕННАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
- •10.1. Момент силы и главный момент системы сил относительно оси
- •10.2. Зависимость между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку
- •10.3. Аналитические выражения моментов силы относительно координатных осей
- •10.4. Приведение пространственной системы сил к данному центру
- •10.5. Возможные случаи приведения пространственной системы сил к данному центру
- •10.7. Выражения главного вектора и главного момента пространственной системы сил через их проекции на оси координат
- •10.8. Уравнения равновесия пространственной системы сил
- •10.9. Теорема Вариньона о моменте равнодействующей пространственной системы сил
- •10.10. Примеры решения задач на приведение пространственной системы сил к простейшему виду
- •10.11. Примеры решения задач на условия равновесия пространственной системы сил
- •11. ЦЕНТР ПРОСТРАНСТВЕННОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
- •11. 1. Сложение системы параллельных сил. Центр параллельных сил
- •11.2. Центр тяжести твердого тела и координаты центра тяжести
- •11.3. Способы определения координат центров тяжести тел
- •11.4. Координаты центров тяжести основных площадей и линий
- •11.5. Примеры решения задач на определение координат центров тяжести сложных плоских фигур

119
10.11. Примеры решения задач на условия равновесия пространственной системы сил
Пример 10. 4
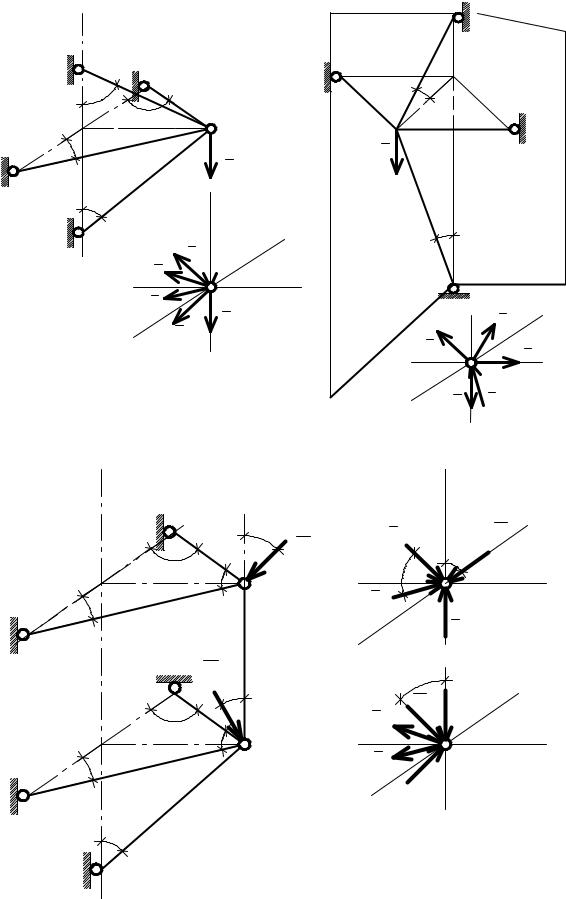
Груз Q весом 200 Н подвешен на тросе ОD перекинутым через блок в точке О (рис. 10. 11, а); удерживается в равновесии двумя горизонтальными стержнями ОВ = ОС и наклонным стержнем ОА. Углы ОВС = ОСВ = 45°;ОАF = 30°; FDО = 60°. Определить, пренебрегая трением на блоке, усилия
в стержнях NОА, NOB и NOC.
Решение:
1.Рассматриваем равновесие груза Q. Для этого освобождаемся от связей,
заменяя их действие на груз Q силами – реакциями связей ТОD, NOB, NOC, NОА.
2.Выбираем оси прямоугольной пространственной системы координат х, у, z и составляем три уравнения равновесия сил (10. 21′), сходящихся в
одной точке в пространстве. Усилие в тросе ТОD = Q, так как трение на блоке не учитывается.
∑Хi = 0 , NOB Соs 45° - NOC Соs 45° = 0
∑Уi = 0 , - Q Sin 60° + NОА Sin 30° - NOB Sin 45° - NOC Sin 45° = 0
∑ Zi = 0 . Q Соs 60° - Q + NОА Соs 30° = 0
3. Решаем систему уравнений и определяем величины усилий в стержнях:
NОА = 115,47 Н ; NOC = NOB = - 81,65 Н.
Знак минус означает, что усилия NOC и NOB имеют направления, противоположные первоначально принятым направлениям.
Пример 10. 5
Груз весом Q = 100 Н подвешен на тросе ОD, перекинутым через блок (рис. 10. 11, б) в точке О и удерживается в равновесии двумя горизонтальными стержнями ОА и ОВ и наклонным стержнем ОС. Плоскость АЕВО – горизонтальная. Стержни имеют длину ОА = 54 см; ОВ = 72 см; ОС = 180 см. Углы наклона троса ОD к плоскости АЕВО - 30° и стержня ОС к вертикали - 30°. Определить, пренебрегая трением на блоке, усилия в стержнях NОА, NOB,
NOC.
Решение:
1.Рассматриваем равновесие груза Q. Для этого освобождаемся от связей,
заменяя их действие на груз Q силами – реакциями связей ТОD, NOB, NOC, NОА.
2.Выбираем оси прямоугольной системы координат хуz в пространстве. Составляем три уравнения равновесия сил, сходящихся в одной точке в
пространстве (10. 21′). Усилие в точке ТОD = Q, так как трением на блоке пренебрегаем.
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
a. |
|
|
|
|
|
б. |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
C |
|
|
|
|
|
|
|
|
|
|
E |
|
0Е |
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
|
||
6 |
45Е |
|
|
|
|
A |
|
Е |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
F |
|
O |
|
|
|
|
O |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|
|
|
|
|
||
5 |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е |
|
|
Q |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
z |
|
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
Е |
|
||
A |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
N OC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
C |
|
|
|
N OB |
|
|
|
y |
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
z |
Q |
|||
|
x |
N OA |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
N OA |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
N OB |
|||
|
|
|
|
|
|
|
|
|
|
O |
|
||
|
|
|
|
|
|
|
|
|
|
|
y |
||
|
|
|
|
|
|
|
|
x |
|
|
Q |
N OC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.10.11 |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
N AF |
|
|
|
|
P1 |
|
|
|
|
|
|
|
Е |
|
|
|
|
|
||
|
|
45Е |
|
|
|
P1 |
|
Е |
|
4 |
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
5 |
|
|
N |
|
|
|
|
|
|
0 |
|
|
|
Е |
||
|
|
0 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
9 |
|
|
A |
|
|
|
|
|
|
y |
|
4 |
|
|
|
|
|
N AD |
|
|
|
|
|||
5 |
|
|
|
|
|
|
|
|
|
|
|
||
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
N AB |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
Е |
|
z |
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
Е |
|
|
4 |
|
|
|
|
||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
E |
45Е |
4 |
|
|
|
|
P1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M |
|
Е |
|
|
B |
|
|
N BE |
|
|
|
|
y |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
9 |
|
|
|
|
|
N BK |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Е
K
4 |
|
5 |
|
|
Е |
C
|
|
|
|
x |
N |
BC |
|
|
|
|
|
Рис. 10.12

121
∑Хi = 0 , - NOА Sin α - NOВ Соs α - Q Соs 30° + NOC Sin 30° = 0
∑Уi = 0 , NOВ + Q Соs 30° Соs α - NOC Sin 30° Соs α = 0
∑ Zi = - Q + Q Sin 30° +NОC Соs 30° = 0
Угол α определяется решением прямоугольного ∆ОЕВ и равен α = 37°. 3. Решаем систему уравнений и определяем величины усилий в стержнях:
NOC = 57,8 Н; NOB = - 46,16 Н; NОА = - 34,62 Н.
Знаки «минус» означают, что усилия NOB и NОА имеют направления, противоположные первоначально принятым направлениям.
Пример 10. 6
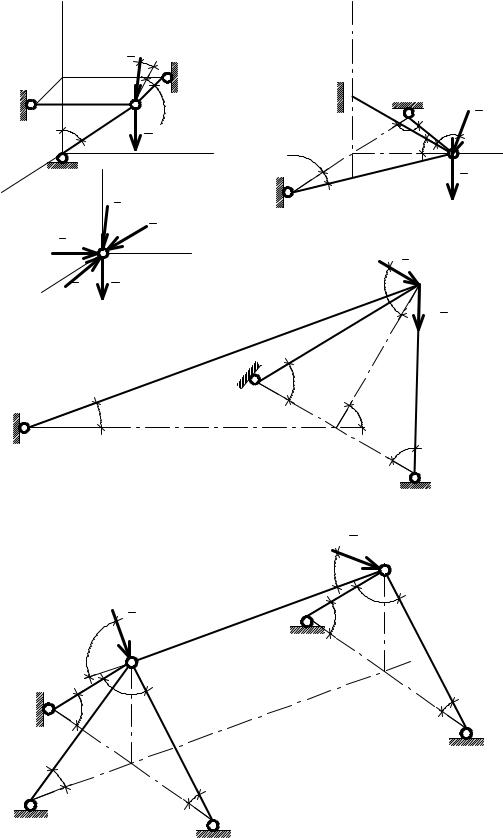
Пространственная ферма, состоящая из шести прямолинейных стержней (рис. 10. 12), находится под действием двух сил Р1 = 1 кН и Р2 = 2 кН, лежащих
вплоскости АВМN, приложенных к узлам А, В, направленных под углом 45° к вертикали. Плоскости равнобедренных прямоугольных треугольников ∆АDЕ, ∆ВКЕ параллельны, а площади равны. Наклоненный стержень ВС, расположен
вплоскости АВMN и имеет угол наклона к вертикали 45°. Определить усилия во всех стержнях фермы.
Решение:
1.Рассматриваем равновесие узлов фермы А и В, находящихся под действием внешних сил Р, 2Р и усилий в стержнях. Для этого освобождаемся от связей, заменяя их действие на узлы усилиями в стержнях NAF, NAD, NAE, NАK, NАС, NАВ.
2.Выбираем оси х, у, z прямоугольной пространственной системы координат и составляем по три уравнения равновесия сил, сходящихся в
одной точке для узлов А и В фермы (10. 21′). Узел А.
∑Хi = 0 , NАF Sin 45° - NAD Sin 45° = 0
∑Уi = 0 , NАF Соs 45° + NАD Соs 45° - Р1 Sin 45° = 0
∑Zi = 0 , NАВ - Р1 Соs 45° = 0
Узел В.
∑Хi = 0 , NВЕ Sin 45° - NВК Sin 45° = 0
∑Уi = 0 , NВЕ Соs 45° + NВК Соs 45° + NВС Sin 45° + Р2 Sin 45° = 0
∑Zi = 0 , NВС Соs 45° - Р2 Соs 45° = 0
3. Решаем систему уравнений и определяем усилия в стержнях фермы:
NАВ = 0,707 кН; NАF = NАD = 0,5 кН;
NВС = 3 кН ; NВЕ = - 2,5 кН .
Знаки минус для усилий в стержнях ВЕ и ВК означают, что направления NВЕ и NВК будут противоположны первоначально выбранным.
Пример 10. 7
Трехстержневой пространственный узел В (рис. 10. 13, а) образован горизонтальными стержнями ВА = 28 см; ВС = 21 см и наклонным стержнем ВD с углом 40° к вертикали. Узел находится в равновесии под действием груза весом Q = 200 Н и силы Р = 60 Н, приложенной под углом 60° к горизонтальной

122
плоскости ОСВА и углом 20° к стержню ВС. Определить усилия в стержнях
NВС, NBА, NВD самостоятельно.
Результаты решения:
NВС = - 155,13 Н, NBА= - 179,5 Н, NВD = 329 Н
Пример 10. 8
Трехстержневой пространственный узел А (рис. 10. 13, б, в), образован тремя стержнями АС, АВ, АD. Узел находится в равновесии под действием груза весом Q = 300 Н и силы Р = 100 Н, приложенной в плоскости АDЕ под углом 70°. Углы наклона стержней АС, АВ и АD показаны на рисунках. Определить усилия в стержнях NАС, NBА, NВD самостоятельно.
Пример 10. 9
Пространственная ферма, состоящая из шести прямолинейных стержней (рис. 10. 14), находится под действием двух сил Р1 = 10 кН и Р2 = 5 кН, лежащих в плоскости АЕFК, приложенных в узлах А, Е, под углами 60° и 30° к стержню АЕ соответственно. Плоскости равносторонних треугольников ∆АСВ, ∆ЕNM параллельны, а площади равны. Наклонный стержень АD расположен в плоскости AEFK и имеет угол наклона к горизонту 60°. Определить усилия во всех стержнях фермы самостоятельно.
Пример 10. 10
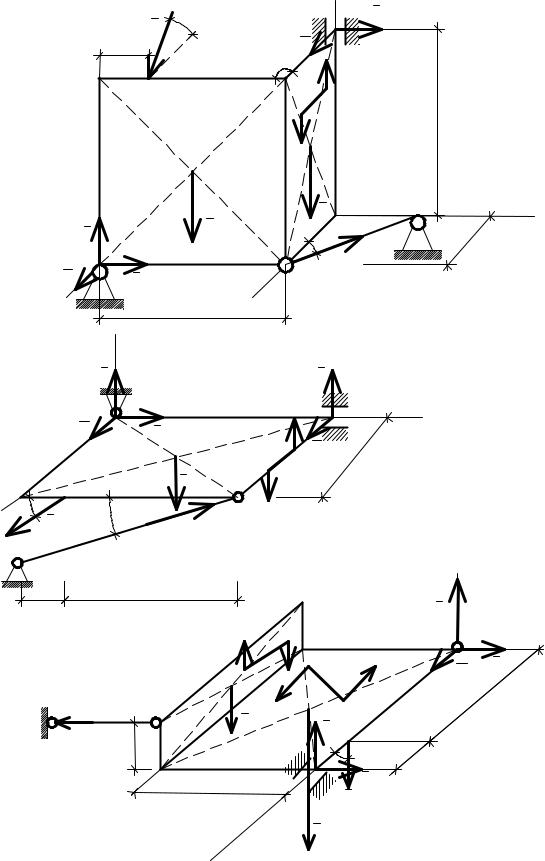
Однородные, тонкие прямоугольные плиты СDFЕ и СВАD жестко соединены под прямым углом, закреплены сферическим шарниром в точке F, цилиндрическим шарниром в точке В и невесомым стержнем DL (рис. 10. 15, а). Веса плит Р1 = 3 кН и Р2 = 6 кН. В плоскости плиты СВАD действует пара сил с моментом М = 2 кНсм. К верхней грани плиты СDFЕ приложена сила Q = 4 кН, линия действия которой параллельна плите СВАD и направлена под углом 60° к горизонту. Определить реакции опор F, В – ХF, УF, ZF, ХВ, УВ и
стержня DL – NDL.
Решение:
1. Рассматриваем плоскости плит, на которые действуют заданная система сил Р1, Р2, F, пара сил с моментом М и силы реакций связей. Реакцию сферического шарнира F раскладываем на три составляющих ХF, УF, ZF;
реакцию цилиндрического шарнира В – на две составляющих ХВ, УВ; реакцию стержня DL - NDL направляем вдоль стержня, полагая, что он растянут.
2.Выбираем оси прямоугольной пространственной системы координат хуz
исоставляем шесть уравнений равновесия произвольной пространственной системы сил (10. 21).
∑Хi = 0 , ХВ - NDL Соs 30° + ХF + Q Соs 60° - NDL Соs 30° = 0
∑Уi = 0 , УВ + NDL Sin 30° + УF = 0
∑Zi = 0 , ZF – Q Sin 60° - Р1 - Р2 = 0
∑Мх = 0 , - УВ . АВ - ZF . FD + Q Sin 60° . 50 + Р2 . FD/2 = 0
∑Му = 0 , ХВ . АВ - ZF . АD + Q Sin 60° . АD + Q Соs 60° . СD + Р2 . АD +
+Р1 . АD/2 + М = 0
∑Мz = 0 , NDL . Sin 30° . АD + Q Соs 60° . СG + ХF . DF+ + УF . АD= 0
а. |
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
0 |
|
|
|
O |
|
P |
|
Е |
|
|
|
|
Е |
||
A |
|
|
|
B |
||
|
|
|
|
0 |
||
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
D |
Е |
|
Q |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
x1 |
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
NBA |
|
|
|
NBC |
|
|
|
B |
|
|
|
|
x |
|
|
|
|
|
|
NBD |
Q |
|
|
||
|
|
|
|
|||
2 0
D |
Е |
|
123
б.
C
 D C
D C
|
|
|
60Е |
|
P |
|
|
|
|
Е |
|
Е |
|
|
|
|
|
0 |
|
|
6 |
|
E |
0 |
7 |
|
|
|
|
|
|
|||
0 |
|
|
|
|||
y1 |
Е |
|
6 |
|
A |
|
|
|
|
|
|||
|
|
|
|
|
||
B |
|
|
|
|
Q |
|
|
|
|
|
|
|
|
y
в. |
P |
A |
7 |
||
0 |
|
|
|
|
Q
C |
Е |
|
|
|
5 |
|
4 |
|
3 |
|
0 |
E |
Е |
4 |
|
|
5 |
B
B
D
0 |
Е |
6 |
|
Е 0 6
6 0
Е
Рис. 10.13
|
|
|
30Е |
|
|
M |
Е |
|
P1 |
0 |
|
|
|
6 |
|
|
A |
|
|
6 |
|
|
|
0 |
|
|
|
|
Е |
|
|
K |
|
Е |
|
0 |
|
|
6 |
|
C
P2
6 |
E |
0 |
|
|
Е |
F
|
Е |
0 |
|
6 |
|
N
Рис. 10.14
|
|
|
|
124 |
|
|
|
|
|
|
а. |
|
6 |
|
|
|
z |
|
yB |
|
|
|
|
|
|
|
|
|
|
|||
Q |
0 |
|
|
|
|
|
|
|||
|
Е |
|
|
|
|
|
|
|
||
|
10 см |
|
|
|
xB |
|
B |
|
|
|
|
|
|
|
|
0Е |
|
|
|
|
|
|
E |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
C M |
|
|
|
|
||
|
G |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
80 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
L |
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
|
|
|
P |
|
|
|
|
|
м |
|
|
|
|
|
|
3 |
|
|
|
||
|
zF |
|
2 |
|
|
|
|
0 |
с |
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
Е_ |
|
0 |
|
|
|
F |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
NDL |
|
|
|
|
|
xF |
yF |
|
|
x |
D |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
60 см |
|
|
|
|
|
|
|
|
б.
x |
C |
0 |
|
|
3 |
|
ЕF |
|
E |
|
1 м |
в. E
z |
|
|
|
|
|
|
|
|
zA |
|
|
|
|
zB |
|
|
|
A |
|
|
|
|
|
|
|
B |
xA |
yA |
|
|
|
xB |
|
|
м |
|
|
|
|
|
|
6 |
||
|
|
|
|
|
M |
|
|
|
L z |
|
P |
|
|
|
|
|
|
|
|
D |
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
6 |
|
|
_ |
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
N DE |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
4 м |
|
|
|
L |
|
|
|
|
|
|
|
M1 |
D |
|
|
|
|
|
|
|
|
|
M2 |
|
|
_ |
K |
|
|
P2 |
|
|
|
|
|
|
|
B |
G |
||||
N КE |
|
|
|
|
z |
|
||
1м |
|
|
|
B |
|
6 |
|
|
|
|
|
|
|
0 |
|||
|
C |
|
|
|
|
|
|
Е |
|
4 |
м |
|
|
|
|
yB |
|
|
|
|
|
|
|
|||
|
|
|
|
|
B |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
P1 |
|
|
|
|
|
|
|
|
|
|
|
|
y
z
zA
 A xA yA
A xA yA
4м
2м
y
у
Рис. 10.15
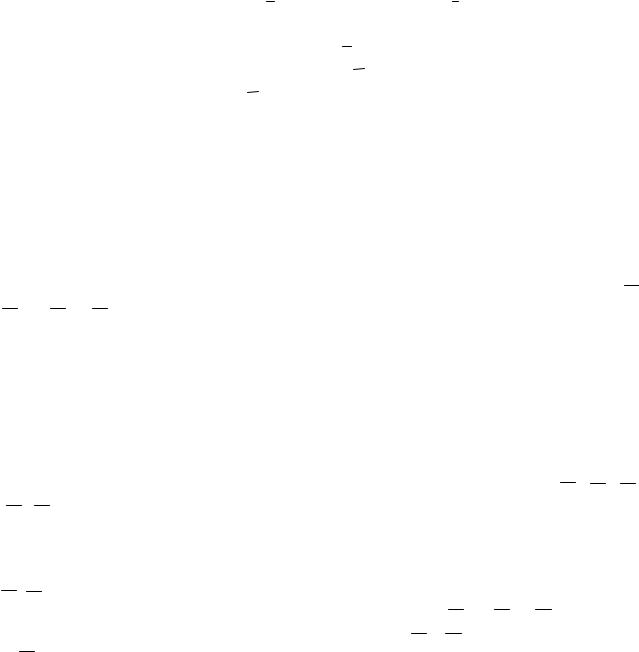
125
3. Решаем систему уравнений: |
|
|
||
|
ХВ - NDL √3/2 + ХF |
+ 4 . 0,5 - NDL√3/2 = 0 |
||
|
УВ + NDL |
. 0,5 + УF = 0 |
|
|
|
|
ZF – 4 . √3/2 – 3 – 6 = 0 |
||
|
- УВ . 80 - ZF |
. 60 + 4 . √3/2 . 50 + 6 . 60/2 = 0 |
||
ХВ . 80 - ZF |
. 100 + 4 . √3/2 . 100 + 4 . 0,5 . 80 + 6 . 100 + 3 . 100/2 + 2 = 0 |
|||
NDL . 0,5 . 100 + 4 . 0,5 . 50 + ХF . 60 + УF . 100= 0 |
||||
и определяем составляющие опорных реакций в сферическом шарнире F: |
||||
ХF = - 9,888 кН ; |
УF = 9,574 кН ; |
ZF = 12,464 кН ; |
||
в цилиндрическом шарнире В: |
|
|
||
|
ХВ = - 0,15 кН ; |
УВ = - 4,933 кН |
||
и в невесомом стержне DL – NDL = - 9,282 кН.
Знак минус означает, что направления составляющих опорных реакций ХF, ХF, ХВ, УВ и NDL будут противоположны первоначально принятым направлениям.
Пример 10. 11
Прямоугольная плита, размером в плане 5 х 6 м, горизонтально расположенная, весом Р = 40 кН, закреплена цилиндрическим шарниром в точке А, цилиндрическим шарниром в точке В и невесомым стержнем ЕD (рис. 10. 15, б). По грани СD в точке L на плиту действует сила F = 10 кН под углом 30° к плоскости плиты, а по грани DВ в плоскости перпендикулярной плите пара сил с моментом М = 2 кНм. Определить реакции опор А, В – ХА, УА, ZА, ХВ, ZВ и стержня DЕ – NDE.
Решение:
1.Рассматриваем равновесие плиты, на которую действуют заданные силы Р, F, пара сил с моментом М и силы реакций связей. Реакцию сферического
шарнира А раскладываем на три составляющих ХА, УА, ZА; реакцию цилиндрического шарнира – на две составляющих ХВ, ZВ; реакцию стержня DЕ
–NDE направляем вдоль стержня, полагая, что он сжат.
2.Выбираем оси прямоугольной пространственной системы координат хуz
исоставляем шесть уравнений равновесия произвольной пространственной системы сил (10. 21).
∑ Хi = 0 ; |
ХА + ХВ = 0 |
∑Уi = 0 ; УА + NDЕ Соs 60° - F Соs 30° = 0
∑Zi = 0 ; ZА + NDЕ Sin 60° + ZB - Р– F Sin 30° = 0
∑Мх = 0 ; ZВ . АВ + NDЕ Sin 60° . CD – F Sin 30° . CL – Р . AB/2 = 0
∑Му = 0 ; - NDЕ Sin 60° . DB + F Sin 30° . DB + Р . DB/2 + М = 0
∑Мz = 0 ; - XB . АB + NDЕ Соs 60° . DB – F Соs 30° . AC = 0
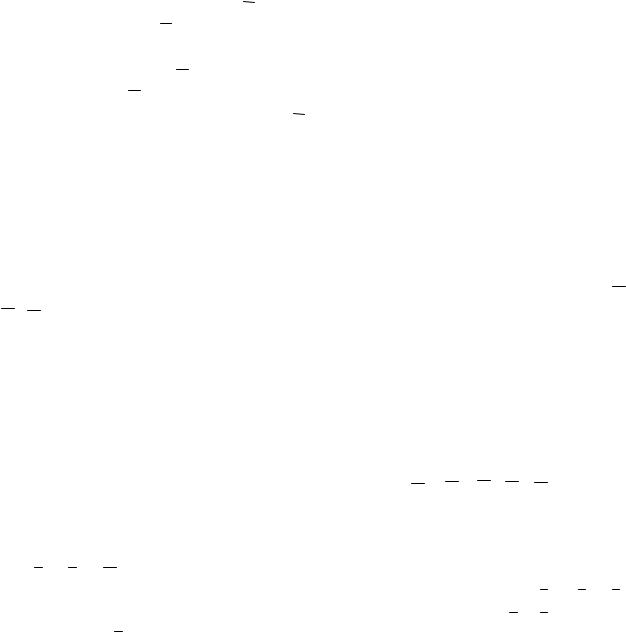
126
3. Решаем систему уравнений:
ХА + ХВ = 0
УА + NDЕ . 0,5 – 10 . √3/2 = 0
ZА + NDЕ √3/2 + ZB - 40 – 10 . 0,5 = 0
ZВ . 5 + NDЕ √3/2. 5 – 10 . 0,5 . 1 – 40 . 5/2 = 0
-NDЕ √3/2 . 6 + 10 . 0,5 . 6 + 40 . 6/2 + 2 = 0
-XB . 5 + NDЕ . 0,5 . 6 – 10 . √3/2 . 6 = 0
иопределяем составляющие опорных реакций в сферическом шарнире А:
ХА = - 7,16 кН ; УА = - 5,967 кН ; ZА = 24,0 кН ;
– в цилиндрическом шарнире В:
ХВ = 7,16 кН ; ZВ = - 4,333 кН
– и в невесомом стержне DЕ – NDE = - 29,253 кН.
Знак минус означает, что направления составляющих опорных реакций ХА, УА, ZВ и NDЕ будут противоположны первоначально принятым направлениям.
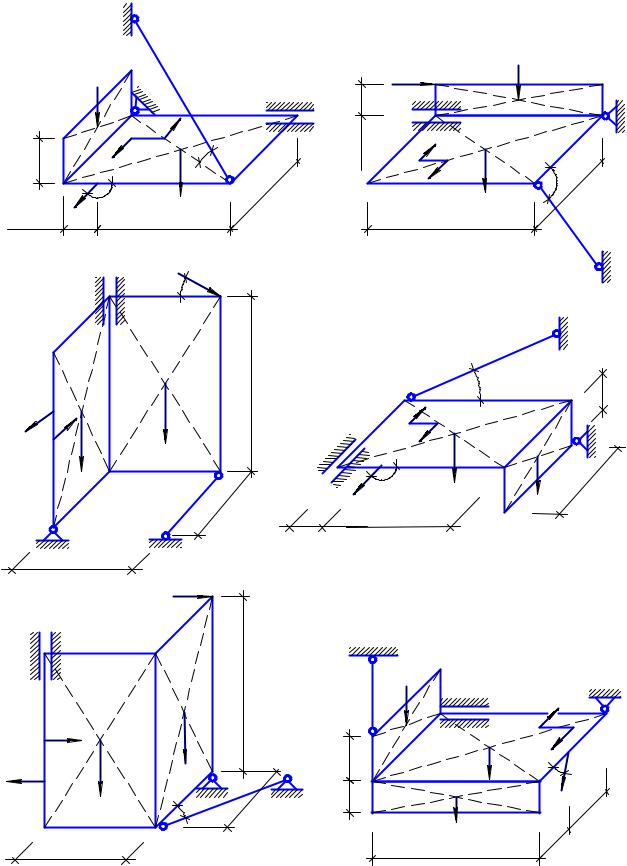
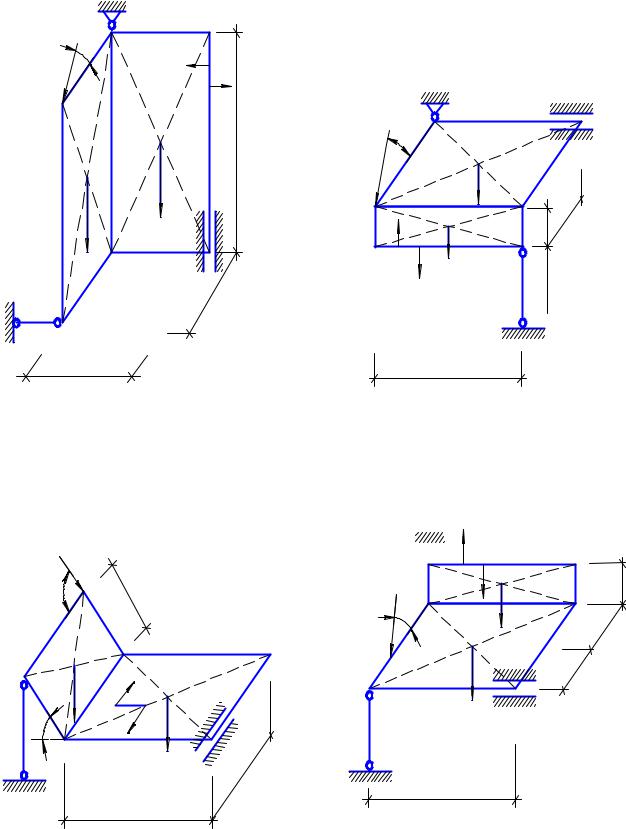
Пример 10. 12
Однородные, тонкие прямоугольные плиты СКLD и СDАВ жестко соединены под прямым углом, закреплены сферическим шарниром в точке А, цилиндрическим шарниром в точке В и невесомым стержнем КЕ (рис. 10. 15, в). Веса плит Р1 = 40 кН и Р2 = 15 кН. В плоскости плиты СКLD действует пара сил с моментом М1 = 2 кНм, а в плоскости СDАВ – пара сил с моментом М2 = 4 кНм. По грани АВ в точке G на плиту действует сила F = 10 кН под углом 60° к плоскости СDАВ. Определить реакции опор А, В – ХА, УА, ZА, УВ, ZВ и стержня
КЕ – NКE.
Решение:
1. Рассмотрим равновесие плит, на которые действуют заданная система сил Р1, Р2, F, пара сил с моментом М и силы реакций связей. Реакцию сферического шарнира А, раскладываем на три составляющих ХА, УА, ZА; реакцию цилиндрического шарнира В – на две составляющих УВ, ZВ; реакцию стержня КЕ – NКE направляем вдоль стержня, полагая, что он сжат.
2.Выбираем оси прямоугольной пространственной системы координат хуz
исоставляем шесть уравнений равновесия произвольной пространственной системы сил (10. 21).
∑Хi = 0 ; ХА + F . Соs 60° = 0
∑Уi = 0 ; УА + УВ - NКЕ = 0
∑Zi = 0 ; ZА + ZВ – Р1 – Р2 – F Sin 60° = 0
∑Мх = 0 ; NКЕ . КC + Р2 . CВ – Р1 . СB/2 = 0
∑Му = 0 ; - ZB . АB – М1 + Р1 . АB/2 + F Sin 60° . GA = 0
∑Мz = 0 ; УB . АB + М2 - NКЕ . АB = 0
|
|
|
|
|
|
|
|
|
|
|
127 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а. |
|
|
H |
|
|
|
|
|
|
|
|
|
|
б. |
_ |
G |
|
_ |
|
|
|
|
|
D |
|
_ |
|
|
|
|
|
|
|
|
B |
|
|
|
F |
|
P2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
P2 |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
M |
|
0Е |
|
|
|
|
10 см |
|
|
|
|
|
|
|
|
|
|
A |
||||
см |
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|||||||
|
_ |
|
6 |
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|||||
10 |
|
|
|
|
|
|
|
|
|
см |
|
|
|
|
|
|
60Е |
|||||||
|
G |
|
|
_ |
|
|
|
|
|
|
|
|
|
|
_ |
|||||||||
|
|
|
|
|
|
|
K |
|
0 |
|
C |
|
|
|
|
|
|
|
м |
|
||||
C |
|
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P1 |
|
|
|
с |
|
|
|||
|
a=150Е P |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||
30 см |
F |
|
40 см |
|
|
|
|
|
|
|
|
|
|
|
60 см |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Е |
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в. |
|
|
5 |
|
|
|
|
|
|
|
|
|
г. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
C |
|
|
|
|
|||
|
_ |
|
|
|
|
|
|
80 |
|
|
|
|
|
|
Е |
|
|
|
см |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
P2 |
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
15 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
P1 |
|
|
|
|
|
|
|
B |
|
G |
|
|
H |
|
|
A |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
D |
|
|
K |
|
|
|
|
|
|
|
|
_ |
|
|
_ |
|
0 с |
м |
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
a=135Е P1 |
|
P2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
8 |
|
|
|
|
||||
|
|
|
|
|
|
0 |
с |
|
|
|
|
20 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
|
E |
|
|
5 |
|
|
|
|
|
|
|
|
40 см |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
40 см |
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
д. |
|
|
|
F |
|
|
|
|
|
|
|
|
е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
B |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см |
|
|
|
|
E |
|
_ |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 P2 |
B |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
A |
|
|
E |
см |
|
|
|
|
_ |
|
|
G |
|
|
|
|
M |
|
_ |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
P2 |
|
|
|
|
|
|
|
15 см |
|
|
|
P |
|
|
_ |
|
|
|
|||
|
|
P1 |
|
4 |
|
|
|
|
м |
|
|
D |
|
_ |
|
S |
|
F |
|
|
|
|
||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
||||
C |
|
|
|
Е |
|
0 |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
H |
|
P2 |
|
L |
|
|
|
|
с |
|||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
60 см |
|
|
|
|
3 |
|
|
|
50 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.16 |
|
|
|
|
|
|
|
|
|
|
|
|
||
128
E
а. |
|
A |
|
D |
б. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
_ |
Е |
|
|
|
|
|
|
|
|
|
F |
|
|
M |
|
|
|
|
B |
|
|
G |
|
|
|
|
A |
|
|||
|
|
|
|
|
|
6 |
|
|
||
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
м |
|
|
Е |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
_ |
|
|
|
|
|
_ |
|
|
|
|
|
C |
|
|
|
|
|
|
G |
|
P1 |
|
||
|
|
|
P1 |
|
|
|
|
|
||
|
|
_ |
|
|
M |
|
|
м |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
с |
||
|
|
P2 |
|
|
|
|
|
_ |
|
0 |
|
|
|
|
|
D |
|
K |
6 |
||
|
|
C |
B |
|
м |
|
P2 |
м |
||
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
с |
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
15 |
|
|
|
5 |
|
|
|
|
E |
||
|
|
|
|
|
|
|
|
|||
|
K |
|
|
|
|
|
|
|
|
|
|
60 см |
|
|
|
|
|
40 см |
|
|
|
|
|
|
|
|
|
|
|
|
||
в.
|
|
_ |
|
|
Е0 |
F |
2 |
|
|
||
|
G |
0 |
|
|
с |
||
|
9 |
|
м |
|
|
|
C |
K |
Е |
_ |
M |
0 |
P2 |
|
|
|
|
||
|
|
|
|
4 |
|
D |
_ |
E |
|
||
|
P1 |
||
|
|
|
70 см |
A 
B м 0с 5
г.
A
6 |
|
0 |
|
|
ЕD |
G
K
E
80 см
M
_
P2
_
P1
B
H
C |
0 см |
|
2 |
|
м |
|
с |
|
0 |
|
3 |
м с 0 2
Рис. 10.17
