76

Пример 7. 7

От заданной нагрузки определить опорные реакции (рис. 7. 16).

Решение:

Расчленяем систему на три части АD, DВЕ и ЕС.

Рассматриваем равновесие диска ЕС, к которому приложен сосредоточенный момент М.

Так момент, т.е. пара сил может быть уравновешена только парой, имеющей противоположное направление вращения и численно равная моменту, получим:

М

Rс = RЕ = ---- . d

Равновесие диска DВЕ рассматривается под действием трех сил: RЕ′ = - RЕ, Rв и RD′, линии действия которых должны пересекаться в точке К, а силовой треугольник, построенный на этих силах, должен быть замкнутым.

Равновесие диска АD рассматривается под действием двух сил: RА и RD = - RD′, т.е. RА = - RD (рис. 7. 16).

Пример 7.8

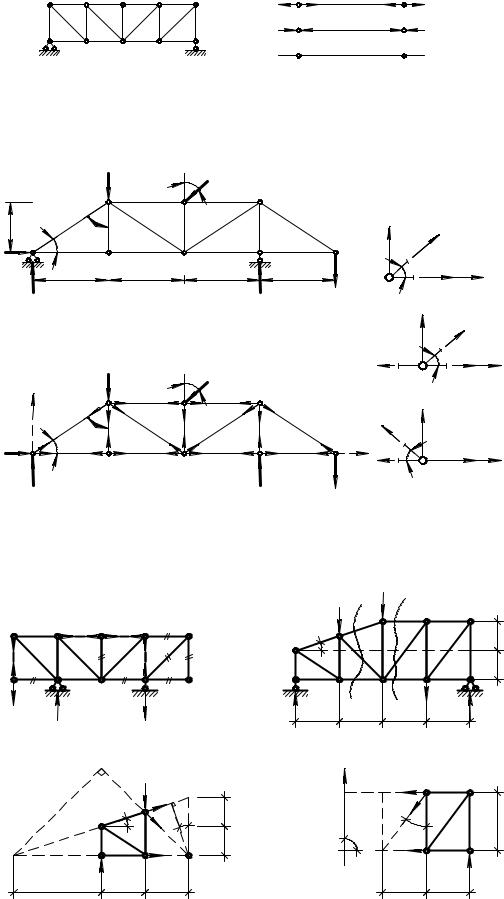
От заданной нагрузки графически определить опорные реакции в следующих системах (рис. 7. 17, 7. 18) самостоятельно.

8.СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ

8.1. Основные понятия о ферме и усилиях в ее стержнях

Фермой называется конструкция, расчетная схема которой представляет собой геометрически неизменяемую систему, состоящую из прямолинейных стержней, соединенных в узлах полными идеальными (без трения) шарнирами.

В реальных фермах стержни в узлах соединяются жестко, а не шарнирно. Однако допущение о шарнирном соединении стержней значительно упрощает расчет ферм. При этом результаты вычислений достаточно точно соответствуют действительности, весом стержней по сравнению с нагрузкой, действующей на ферму, можно пренебречь и рассматривать их как невесомые. Нагрузка обычно прикладывается в узлах фермы.

При узловой нагрузке в прямолинейных стержнях фермы возникают только продольные реакции или усилия N, вызывающие растяжение или сжатие стержней. Определение усилий в стержнях является одной из основных задач при расчете ферм.

Ферма называется плоской, если оси всех ее стержней лежат в одной плоскости, совпадающей с плоскостью действия внешних сил (с силовой плоскостью). Ниже рассматривается расчет только плоских ферм.

Стержни плоской фермы (рис. 8. 1, а), расположенные по внешнему контуру образуют верхний и нижний пояс фермы, а стержни, соединяющие их, образуют решетку фермы. Вертикальные стержни решетки называются стойками, а наклонные – раскосами.

77

На каждый стержень фермы (рис. 8. 1, б) со стороны узлов действует уравновешенная система сил (F1 = - F2, F1 = F2 = F), направленных вдоль оси стержня. Эти силы вызывают либо растяжение, либо сжатие стержня. Согласно аксиоме действия и противодействия усилие N стержня при растяжении направлено от узлов, а при сжатии – к узлам. При этом модуль усилия N = F1 =

=F2 = F. Если узлы не оказывают силового воздействия на стержень, т.е. F1 =

=F2 = 0, то усилие в нем отсутствует (N = 0).

8.2. Условие геометрической неизменяемости и статической определимости фермы

Необходимым условием геометрической неизменяемости фермы является равенство:

где С – число стержней, а У – число полных шарнирных узлов фермы. Действительно, один стержень, который является неизменяемой частью

фермы, имеет два узла, а последующие узлы фермы присоединяются двумя стержнями, не лежащими на одной прямой. Таким образом, общее число

стержней в геометрически неизменяемой ферме равно:

С = (У – 2) . 2 + 1 = 2У – З .

Чтобы усилия в стержнях фермы определялись только методами статики, она должна быть статически определимой. Условие статической определимости фермы то же самое, что и условие ее геометрической неизменяемости (8. 1).

В самом деле, рассматривая плоскую геометрически неизменяемую ферму, как одно твердое тело под действием произвольной системы сил, будем иметь три неизвестных опорных реакции и С неизвестных усилий в стержнях фермы, т.е. всего неизвестных будет С + З. При этом для каждого узла фермы, находящегося под действием сходящихся сил (усилий, опорных реакций или активных сил), можно составить только два уравнения равновесия статики:

n n

∑ Хi = 0 , ∑ Уi = 0 ,

i=1 i=1

а всего таких уравнений будет 2У. Приравнивая число неизвестных числу уравнений, получаем условие статической определимости фермы:

С + З = 2У ,

или

79

8.3. Методы расчета фермы

Для определения усилий в стержнях статически определимых ферм разработаны различные аналитические и графические методы. С появлением быстродействующих электронных вычислительных машин (ЭВМ) в настоящее время преимущественно используются аналитические методы расчета ферм. Рассмотрим два наиболее простых из них: метод вырезания узлов и метод сечений (метод Риттера).

8.3.1. Метод вырезания узлов

Суть метода состоит в том, что при определении усилий в стержнях фермы рассматривают равновесие каждого узла, мысленно вырезая его из фермы. Влияние рассеченных стержней на узел заменяют их усилиями, предполагая при этом, что все стержни фермы испытывают растяжение, т.е. усилия изображают стрелками от узлов (рис. 8. 1, б). Если в результате вычислений усилие получается со знаком «плюс», то стержень действительно растянут, если со знаком «минус», то стержень не растянут, а сжат.

Искомые усилия определяют из уравнений равновесия сил, приложенных к рассматриваемому узлу:

n n

Поскольку для каждого узла плоской фермы можно составить только два уравнения равновесия, то расчет начинают с двухстержневого узла (число неизвестных должно быть равно числу уравнений), переходя затем к следующим узлам, где с учетом найденных усилий неизвестны снова два усилия. Если предварительно определить опорные реакции фермы, рассматривая ее, как одно твердое тело, то согласно выражению (8.1) для определения усилий во всех стержнях потребуется 2У – З уравнений вида (8.2), т.е. необходимость в составлении трех последних уравнений отпадает. Однако, составив их в качестве проверки, полезно убедиться, что эти уравнения обращаются в тождества.

Недостатком метода вырезания узлов является то, что погрешности вычислений накапливаются от узла к узлу и при грубых вычислениях проверка равновесия последнего по ходу расчета узла фермы не будет выполняться.

Пример 8. 1

Определить методом вырезания узлов усилия в стержнях плоской статически определимой фермы (рис. 8. 2, а), если Р1 = 12 кН, Р2 = 8 кН, Р3 = 14 кН.

Решение:

1. Проверяем выполнение условия (8. 1).

Число стержней в ферме С = 13, а число шарнирных узлов У = 8, т.е. получаем: С = 2У – З, 13 = 2 . 8 – 3, 13 = 13. Следовательно, ферма является геометрически неизменяемой и статически определимой.

80

2. Определяем реакции опор фермы ХА, УА и Rв, составляя уравнения равновесия статики:

∑Х= 0 , ХА + Р2 Sin 60° = 0 ,

∑У= 0 , УА – P1 – Р2 Соs 60° + Rв – Р3 = 0 ,

∑МА = 0 , – P1 . 4 + Р2 Sin 60° . 3 – Р2 Соs 60° . 8 + Rв . 12 – Р3 . 16 = 0 ,

откуда,

Rв = 10,268 кН , УА = 9,732 кН , ХА = 6,928 кН .

Проверка:

∑М4 = 0 ,

∑М4 = ХА . 3 – УА . 8 + P1 . 4 + Rв . 4 – Р3 . 8 = 6,928 . 3 – 9,732 . 8 + 12 . 4 +

+10,268 . 4 – 4 . 8 = 109,856 – 109,856 = 0

Следовательно, реакции опор определены верно.

3. Определяем усилия в стержнях фермы, рассматривая равновесие каждого ее узла (рис. 8. 2, б), начиная с двухстержневого узла 1. Нумерацию узлов 1, 2 …, 8 составляем так, чтобы при переходе от одного узла к другому в нем были неизвестны только два усилия. В каждом узле искомые усилия

Узел 7: ∑ Х= - N8 – N9 Соs α + N12 Соs α = 0 ,N12 = 6,667 кН