
- •1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
- •1.1. Содержание курса «Сопротивление материалов»
- •1.2. Основные допущения о свойствах материалов и характере деформирования
- •1.3. Геометрическая схематизация элементов конструкций
- •1.4. Классификация нагрузок
- •1.5. Понятие о внутренних силах
- •1.6. Внутренние силы в поперечном сечении бруса
- •1.7. Напряжения. Связь между напряжениями и внутренними силами в поперечном сечении бруса
- •1.8. Понятие о деформациях
- •1.9. Простейшие типы деформации бруса
- •2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
- •2.1. Статические моменты сечений
- •2.2. Моменты инерции сечений
- •2.3. Моменты инерции простейших сечений
- •2.4. Преобразование моментов инерции при параллельном переносе осей
- •2.5. Преобразование моментов инерции при повороте осей
- •2.6. Главные оси инерции. Главные моменты инерции
- •2.7. Моменты сопротивления сечений
- •2.8. Радиусы инерции
- •3. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛ В СЕЧЕНИЯХ СТЕРЖНЕЙ. ЭПЮРЫ ВНУТРЕННИХ СИЛ
- •3.1. Внутренние силы в сечениях бруса (стержнях). Их связь с нагрузкой
- •3.2. Построение эпюр внутренних сил
- •3.3. Построение эпюр внутренних сил в балках
- •3.4. Построение эпюры продольных сил
- •3.5. Построение эпюры крутящих моментов
- •4. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ (ЦРС)
- •4.1. Напряжения деформации при ЦРС. Закон Гука
- •4.2. Определение перемещений при ЦРС
- •4.4. Механические свойства материалов. Диаграммы растяжения и сжатия
- •4.5. Расчет на прочность при растяжении (сжатии)
- •5. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
- •5.1. Напряженное состояние в точке нагруженного твердого тела
- •5.2. Плоское напряженное состояние
- •5.3. Обобщенный закон Гука. Связь между напряжениями и деформациями
- •6. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ (ИЗГИБ БАЛОК)
- •6.1. Определение напряжений в балке
- •6.2. Расчет балок на прочность по допускаемым напряжениям
- •Литература
12
Продольная сила N в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на продольную ось бруса z всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Поперечные силы Qx и Qy в произвольном поперечном сечении бруса численно равны алгебраической сумме проекций на оси поперечного сечения бруса х и у всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
Изгибающие моменты Мx и Мy в произвольном поперечном сечении бруса численно равны алгебраической сумме моментов относительно осей поперечного сечения бруса х и у всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
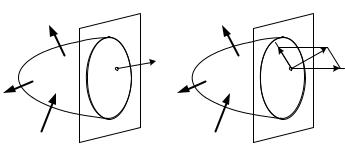
Крутящий момент Мz в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов относительно продольной оси бруса z всех внешних сил, приложенных по одну сторону от рассматриваемого сечения.
1.7. Напряжения. Связь между напряжениями и внутренними силами в поперечном сечении бруса
Внутренние силы, как уже указывалось, распределены по сечению тела (в частности, бруса) сплошным образом, при этом в общем случае их значение и направление в отдельных точках сечения различны. Для суждения об интенсивности внутренних сил в определенной точке данного сечения вводится понятие напряжения.
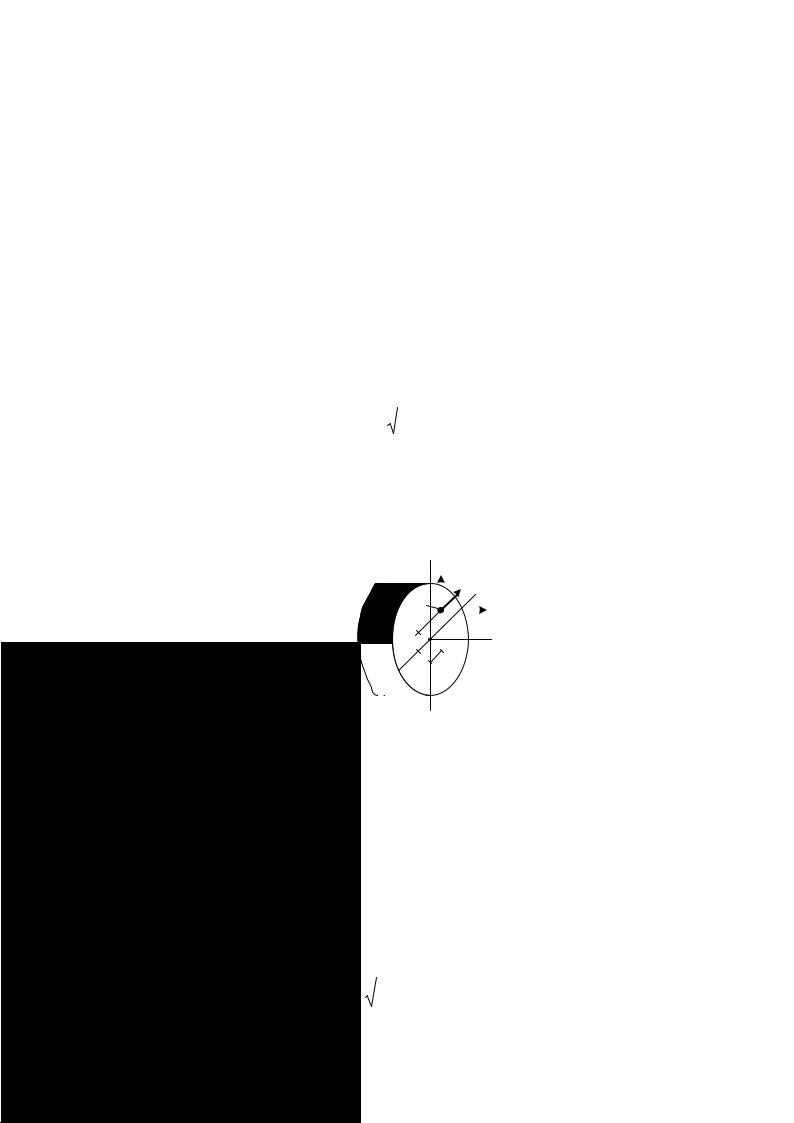
Выделим в окрестности интересующей нас точки сечения малую площадку, площадью ∆А. Допустим, что на этой площадке возникает внутренняя сила ∆R (рис. 1.7 а).
Рис. 1.7
Отношение этой внутренней силы к площади выделенной площадки называется средним напряжением рср в окрестности рассматриваемой точки по проведенному сечению (по площадке ∆А):
рср |
|
= ∆R/∆А. |
(1.3) |
Впределе при стремлении ∆А к нулю получим истинное напряжение
вданной точке рассматриваемого сечения:
14
Умножая напряжения σz,, τ zx,, τ zy на площадь dA площадки их дейст-
вия, получим элементарные внутренние силы: |
dQy = τ zy dA. |
|
|
dN = σz dA, |
dQx = τ zx dA, |
|
|
Суммируя эти элементарные силы по всей площади сечения, получим |
|||
выражения составляющих главного вектора внутренних сил в сечении: |
|
||
N = ∫σz dA , |
Qx = ∫τzx dA , |
Qy = ∫τzy dA . |
(1.6) |
A |
A |
A |
|
Умножая каждую из элементарных сил на расстояние до соответствующей оси, получим элементарные моменты внутренних сил:
dMx = dN·y = (σz dA)y,
dMy = dN·x = (σz dA)x, dMz = dQy·x-dQx·y = ( τ zy dA)х τ-zx dA)y.
Суммируя элементарные моменты по всей площади сечения, получим выражения для составляющих главного момента внутренних сил:
M x = ∫σz y dA, |
M y = ∫σz x dA, |
M z = ∫( τzy x dA − τzx y dA ). |
(1.7) |
A |
A |
A |
|
Таким образом, задача сопротивления материалов об определении напряжений, возникающих в поперечных сечениях бруса при различных видах его нагружения, состоит в следующем: с помощью метода сечений определяем внутренние силовые факторы, а затем из полученных формул находим напряжения.
1.8. Понятие о деформациях
Под действием нагрузки тело деформируется, т.е. его формы и размеры изменяются. Деформация состоит из двух частей: упругой, обратимой деформации, которая исчезает после удаления нагрузки, и неупругой, остаточной деформации, которая не исчезает после удаления нагрузки.
Неупругая деформация, которая не сопровождается разрушением, на-
зывается пластической деформацией.
Деформации тела могут развиваться с течением времени при неизменной нагрузке. Такие деформации называются деформациями ползучести.
y
c
\2 |
dx
c*
 b*
b*
y
d
\2- xy |
|
x |
d |
+ |
d |
|
|
|
|
x |
|
|
d |
|
a* |
b
x
Рис. 1.9

15
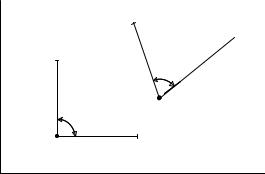
Термин «деформация» употребляют в сопротивлении материалов в двояком смысле: в первом - под деформацией подразумевают изменение формы и размеров тела, во втором – под деформацией рассматривают изменение длин и углов в окрестности точки тела. Рассмотрим такие деформации.
Мысленно через точку а тела проведем бесконечно малые отрезки, параллельные осям координат (положение a, b, c). Длина этих отрезков равна dx, dy, dz. На рис. 1.9 показаны эти отрезки только в плоскости ху. При деформировании тела эти отрезки перемещаются (положение a*, b*, c*), при этом длины отрезков и углы между ними изменяются.
Изменение длин отрезков ∆x, ∆y, ∆z называются абсолютными линейными деформациями. Отношение приращения длин отрезков к перво-
начальной длине называется относительной линейной деформацией:
εx = |
d x |
, |
εy = |
d y |
, |
εz = |
d z |
. |
(1.8) |
d x |
d y |
|
|||||||
|
|
|
|
|
d z |
|
|||
Изменение первоначально прямого угла между отрезками ab и ac после приложения нагрузки к телу, выраженное в радианах, представляет собой угловую деформацию γху в точке а в плоскости ху. Аналогично, γyz и γzх представляют собой угловые деформации в плоскостях yz и zx.
Деформации тела в каждой его точке по любым направлениям могут быть определены, если известны линейные εx, εy, εz и угловые γху, γyz, γzх деформации.
Линейные и угловые деформации – величины безразмерные.
1.9. Простейшие типы деформации бруса
При произвольной форме тела его деформации могут быть весьма разнообразными. Для бруса можно указать несколько простейших типов деформаций, возникающих при определенном способе приложения внешних сил.
Рассмотрим эти простейшие деформации бруса.
Рис. 1.10
1. Осевое растяжение или сжатие (рис. 1.10 а).
При осевом растяжении или сжатии в поперечных сечения бруса возникают только продольные силы N. Брус, испытывающий растяжение или
