
- •1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
- •1.1. Содержание курса «Сопротивление материалов»
- •1.2. Основные допущения о свойствах материалов и характере деформирования
- •1.3. Геометрическая схематизация элементов конструкций
- •1.4. Классификация нагрузок
- •1.5. Понятие о внутренних силах
- •1.6. Внутренние силы в поперечном сечении бруса
- •1.7. Напряжения. Связь между напряжениями и внутренними силами в поперечном сечении бруса
- •1.8. Понятие о деформациях
- •1.9. Простейшие типы деформации бруса
- •2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
- •2.1. Статические моменты сечений
- •2.2. Моменты инерции сечений
- •2.3. Моменты инерции простейших сечений
- •2.4. Преобразование моментов инерции при параллельном переносе осей
- •2.5. Преобразование моментов инерции при повороте осей
- •2.6. Главные оси инерции. Главные моменты инерции
- •2.7. Моменты сопротивления сечений
- •2.8. Радиусы инерции
- •3. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛ В СЕЧЕНИЯХ СТЕРЖНЕЙ. ЭПЮРЫ ВНУТРЕННИХ СИЛ
- •3.1. Внутренние силы в сечениях бруса (стержнях). Их связь с нагрузкой
- •3.2. Построение эпюр внутренних сил
- •3.3. Построение эпюр внутренних сил в балках
- •3.4. Построение эпюры продольных сил
- •3.5. Построение эпюры крутящих моментов
- •4. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ (ЦРС)
- •4.1. Напряжения деформации при ЦРС. Закон Гука
- •4.2. Определение перемещений при ЦРС
- •4.4. Механические свойства материалов. Диаграммы растяжения и сжатия
- •4.5. Расчет на прочность при растяжении (сжатии)
- •5. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
- •5.1. Напряженное состояние в точке нагруженного твердого тела
- •5.2. Плоское напряженное состояние
- •5.3. Обобщенный закон Гука. Связь между напряжениями и деформациями
- •6. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ (ИЗГИБ БАЛОК)
- •6.1. Определение напряжений в балке
- •6.2. Расчет балок на прочность по допускаемым напряжениям
- •Литература
68
4.ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ (ЦРС)
4.1.Напряжения деформации при ЦРС. Закон Гука
Вряде элементов строительных конструкций возникают только продольные усилия, которые вызывают в них деформацию растяжения или сжатия. Например, трос подъемника при подъеме груза растянут, колонны здания преимущественно сжаты, элементы форм могут быть растянутыми или сжатыми.
Всамом простом случае растянутый или сжатый стержень – это стержень, на который действуют силы, приложенные к его концам и направленные вдоль его оси, то есть в поперечных сечениях стержня имеется только одна продольная (нормальная) сила N.
Для вычисления нормальных напряжений σΖ , характеризующих интен-
сивность внутренних сил в поперечном сечении, используем известную из главы 1 (формула 1.6) зависимость:
Ν = ∫σΖ dA |
4.1 |
А |
|
Согласно гипотезе плоских сечений, поперечные сечения, плоские до нагружения, остаются плоскими и при нагружении. Представим себе стержень состоящим из продольных волокон. Так как все продольные волокна деформируются одинаково, то нормальные напряжения, вызывающие эти
деформации, также должны быть одинаковы ( σΖ = const). Вынося σΖ за
знак интеграла в формуле 4.1, получим: |
|
|
N = σΖA , |
4.2 |
|
откуда находим |
N . |
|
σΖ = |
4.3 |
|
|
A |
|
Растягивающие напряжения считаются положительными, а сжимающие
– отрицательными. Таким образом, знак напряжения σΖ совпадает со знаком
продольной силы N.
Если в рассматриваемом сечении имеется отверстие или вырез, то напряжения определяют по формуле
σΖ = |
N |
4.4 |
|
A нт |
|||
|
|
где Ант – площадь поперечного сечения «нетто» с учетом ослабления.

69
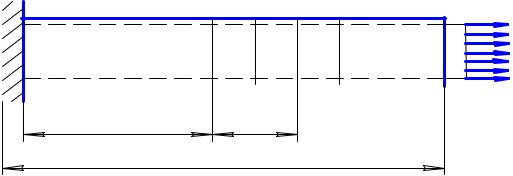
При действии продольных сил стержень деформируется. Рассмотрим прямой стержень постоянного сечения, во всех сечениях которого действует продольная сила N = F (рис. 4.1).





 F z
F z
l
l1
y |
в 1 |
|
h 1 |
x |
h |
|
||
|
в |
|
Рис. 4.1
При растягивающей силе F длина стержня l увеличивается до значения l1, а поперечные до значений b1 и h1. Деформация стержня:
l=l1 −l – абсолютная продольная деформация;
в = b1 – b2 ; h = h1 – h2 – абсолютные поперечные деформации. Относительная продольная деформация определяется:
|
εпрод = ε Z = |
l . |
|
|||
|
|
|
|
l |
|
|
Относительные поперечные деформации: |
|
|||||
ε х = |
b |
, εy = |
|
h |
. |
4.6 |
|
|
|
||||
|
b |
h |
|
|||
Для изотропных материалов ε х = εу.
Деформации εх, εу, εz называются также линейными деформациями и являются безразмерными величинами.
Закон Гука, определяемый экспериментом, для растяжения (сжатия)
имеет вид: |
|
σz =Eεz |
4.7 |
Коэффициент пропорциональности Е в формуле 4.7 – модуль нормальной упругости. Он является физической постоянной материала и определяется экспериментально. Так как деформация z величина безразмерная, то Е имеет размерность напряжения. Для углеродистой стали Е = 2. 105 МПа, для меди Е = 1. 105 МПа, для дерева Е = 104 МПа. Закон Гука справедлив только при упругой работе материала.
Поперечная деформация зависит от продольной. Экспериментально установлено, что при растяжении или сжатии в пределах упругих деформаций отношение поперечной деформации к продольной является постоянным для каждого материала. Абсолютная величина этого отношения называется коэффициентом Пуассона (обозначается ν или μ):
|
|
70 |
|
||
ν = − |
εy |
= − |
εx . |
4.8 |
|
εz |
|||||
|
|
εz |
|
||
Для различных материалов значения коэффициентов Пуассона находятся в пределах 0 < ν < 0,5. Например, для большинства металлов 0,25 < ν < 0,35.
Найдем изменение размеров однородного растянутого (сжатого) стерж-
ня. |
|
|
|
|
σΖ = |
Ν |
|
|
Из формулы 4.5 имеем |
l=εz l , а из 4.7 и 4.3 |
εΖ = |
. Тогда |
|||||
ΑΕ |
||||||||
|
|
Νl |
|
|
Ε |
|
||
|
l = |
. |
|
|
|
4.9 |
||
ΕΑ
где N – продольная сила на участке стержня длиной l; А – площадь поперечного сечения;
E – модуль упругости.
Зависимость 4.9 используется в тех случаях, когда на участке стержня длиной l значения N и А постоянны.
Произведение ЕА называют жесткостью сечения стержня при растяжении (сжатии).
Сужение сечения стержня (рис. 4.1) на основании формул 4.3, 4.6, 4.7,
4.8:
b = εΧb = −ν |
σΖ b = −ν Νb |
, |
|||
|
|
Ε |
|
ΕΑ |
|
h = εyh = −ν |
σΖ |
h = −ν |
Νh . |
4.10 |
|
|
|
Ε |
|
ΕΑ |
|
4.2. Определение перемещений при ЦРС
Рассмотрим стержень, нагруженный на свободном конце равномерно распределенной по сечению продольной нагрузкой (рис. 4.2). Выделим два произвольных сечения а-а и b-b, отстоящих друг от друга на расстоянии dz.
a a1 b b1 sz
|
a1 |
|
1 |
a |
dz |
b |
b |
z |
|
|
l
Рис. 4.2
71
От действия нагрузки сечение а-а переместится в положение а1-а1 на расстояние аа1=w(z), а сечение b-b переместится в положение b1-b1 на расстояние bb1=w(z)+dw. Следовательно, абсолютное удлинение участка стержня
длиной dz равно dz=dw, а относительное удлинение: |
|
||||||||
εΖ = dw . |
|
|
|
|
|
|
|
4.11 |
|
|
dz |
|
|
|
|
|
|
|
|
В соответствии с законом Гука (4.7) и формулой (4.3) записываем выра- |
|||||||||
жение (4.11) в виде: |
σΖ = |
|
Ν |
|
= dw |
|
|
||
εΖ = |
|
, |
4.12 |
||||||
|
ΕΑ |
||||||||
то есть |
Ε |
|
|
dz |
|
|
|||
dw |
|
|
Ν |
|
|
|
|
||
|
= |
|
, |
|
4.13 |
||||
или |
dz |
ΕΑ |
|
||||||
|
|
|
|
|
|||||
ΕΑdw = Ν. |
|
|
|||||||
|
|
4.14 |
|||||||
dz
Интегрируя уравнение 4.14, получаем выражение для определения перемещения произвольного сечения:
w(z)= Ζ∫ Νdz + C .
0 ΕΑ
Постоянную интегрирования С найдем из условия, что при z = 0, w(0) = wo. Отсюда следует, что С = w(o) = wo – перемещение левого сечения стержня.
Окончательно получаем:
|
|
w(z)= w + ∫ Νdz . |
||
|
|
|
|
z |
|
4.15 |
|
o |
0 ΕΑ |
|
|
|
|
|
Если на участке интегрирования σz = Ν |
= const , то |
|
||
|
Α |
Νz |
|
|
|
w(z)= wo + |
|
4.16 |
|
|
|
ΕΑ |
|
|
Перемещения на этом участке, следовательно, изменяются по линейной |
||||
зависимости, а деформация |
εz = dw = const . Полное удлинение можно опре- |
|||
|
dz |
|
|
|
делить по формуле 4.9.
Если же стержень нагружен продольной нагрузкой так, что имеется несколько участков, то постоянные интегрирования (то есть перемещения в началах участков) определяют из условий сопряжения участков – условий непрерывности функции перемещений при переходе от одного участка к другому. Правило знаков для продольных перемещений следующие: положительными считаются перемещения, направленные вдоль положительного направления оси z.
Пример 4.1.

72
Для стержня, показанного на рис. 4.3, построить эпюру перемещений w(z).
1 2
z1 |
|
3F |
z2 |
2F |
c1 |
|
c2 |
|
|
|
2a |
|
3a |
|
F |
+ |
|
Эпюра N |
|
|
- |
2F |
||
2Fa |
|
|
||
|
|
Эпюра W |
|
|
EA |
|
+ |
4Fa |
|
|
|
|
- |
EA
Рис. 4.3
Решение. Разобьем стержень на два участка: I и II. Определим продольные силы на каждом участке и выберем локальные системы координат с началом в точках с1 и с2 . Запишем перемещения для участков I и II, используя выражение (4.16), так как σz = const .
|
Участок |
I: 0 < z1 |
< 2а. N1=F; w1 = wc |
+ |
Fz1 |
|
; |
здесь wc1 = 0. Тогда |
|||||||||||||
|
ΕΑ |
||||||||||||||||||||
|
|
Fz1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
w1 |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ΕΑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Участок II: 0 < z2 < 3а. N2=-2F; w |
2 |
= w |
c2 |
− |
2Fz2 |
|
|
. Значение w |
c2 |
найдем |
||||||||||
|
|
|
|
||||||||||||||||||
из условия сопряжения: |
|
|
|
|
|
ΕΑ |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
при z1 = 2а и z2 = 0: |
2Fа |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
w12(а) = wc2 ; wc2 = |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
. Следовательно: |
|
|
|
|
|
|
|
|
|
||||||||||
|
ΕΑ |
|
|
|
|
|
|
|
|
|
|||||||||||
|
w2 = |
2Fа |
− |
2Fz2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ΕΑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ΕΑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При z2 = 3а получаем w2(3а) = − 4FΕΑа .
Решим пример 4.1 другим способом. Сечение с2 (рис. 4.3) переместится в результате деформации участка с1с2:

73
w(2а)= 3FΕΑ2а − 2FΕΑ2а = 2ΕΑFа .
Сечение с2 перемещается вправо. Крайнее правое сечение переместится в результате деформации участка с1с2 от силы 3F и от сжатия силой 2F всего стержня:
w(5а)= 3FΕΑ2а − 2FΕΑ5а = 4ΕΑFа .
Крайнее правое сечение переместится влево.
Пример 4.2.
Жесткий брус СВ, деформацией которого можно пренебречь, подвешен на двух тягах круглого сечения длиной l= 1,5 м (рис. 4.4, а). Левая тяга диаметром d1 = 2 см выполнена из алюминия, правая – диаметром d2 = 2,5 см – из стали. Определить усилия, напряжения и удлинения тяг.
а) |
y |
|
l |
1 |
2 |
с=2м |
в=1м |
|
|
c |
в |
F=150кН |
б)
N1 |
с |
N2 |
c |
в |
|
|
в |
|
|
|
F |
Рис. 4.4
Решение. Для определения усилий в тягах составляем два уравнения равновесия бруса СВ (рис. 4.4, б):
∑mв = 0; - N1(c + в) + F. в = 0; Ν1 = сF+вв =50кH .
∑mс = 0; N2(c + в) - F. с = 0; Ν2 = сF+св =100кH .
Напряжения определяем по формуле 4.3:
σ1 = Ν1 = 4Ν1 =159мПа;
Α1 πd12
σ2 = 4πΝd22 = 204мПа.
2
Удлинения находим в соответствии с 4.9:
l |
1 |
= |
Ν1l |
=3,41мм; |
|
|
|||||
|
|
Ε Α |
1 |
|
|
|
|
|
1 |
|
|

74
l2 = Ν2l =1,49мм.
Ε2 Α2
4.3.Статически неопределимые системы с растянутыми (сжатыми)
стержнями
Выше были рассмотрены стержни и стержневые системы, внутренние усилия в которых от заданной нагрузки могли быть определены при помощи уравнений равновесия. Такие стержни и системы называются статически определимыми. В отличие от них статически неопределимыми называются стержни и системы стержней, усилия в которых не могут быть определены при помощи одних лишь уравнений равновесия. При расчете в данном случае необходимо составлять дополнительные уравнения (уравнения совместимости перемещений), учитывающие деформации стержней. Число дополнительных уравнений, которые необходимо составить для расчета системы, характеризует степень ее статической неопределимости.
Статически неопределимые системы имеют ряд особенностей по сравнению со статически определимыми. Усилия в стержнях статически определимых систем возникают только от действия внешней нагрузки. В стержнях же статически неопределимых систем усилия могут возникать и при отсутствии внешней нагрузки – в результате изменения температуры, неточности изготовления отдельных элементов конструкции, смещения опор.
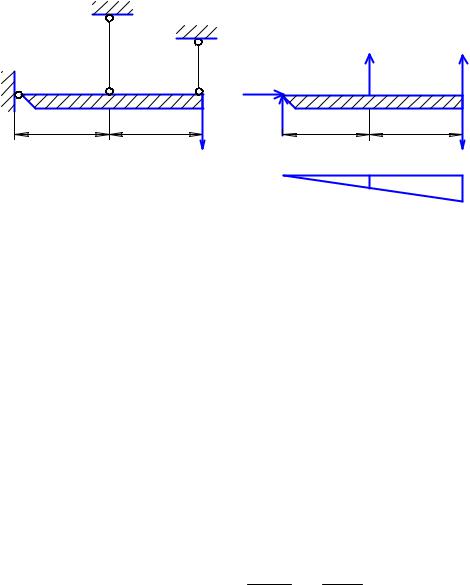
Пример 1. Рассмотрим стержень, закрепленный с двух сторон и находящийся под действием сосредоточенной силы (рис. 4.5, а).
a) |
1 |
|
б) |
в) N |
г) s д) W |
|
|
1 |
F |
F |
|
|
R |
|
R |
4 |
4А |
|
|
|
|
||
EA |
F |
a |
F |
3F |
F |
|
|
|
|
4 |
4А |
3EA |
Z |
a |
|
|
Fa |
|
|
4EA |
|||
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
Рис. 4.5 |
|
|
В точках закрепления стержня возникают опорные реакции R1 и R2, на- |
||||
правленные вдоль его оси. Составим уравнение равновесия: |
|||||
|
|
|
|
∑Ζ = 0 ; R1 + R2 = F. |
4.17 |
Уравнение содержит два неизвестных. Стержень является один раз статически неопределимым. Дополнительное уравнение составим исходя из условия, что длина стержня при его деформировании не изменяется, то есть l = 0 . Отбросим мысленно любое из закреплений, например, верхнее (рис.

75
4.5, б) и рассмотрим действие сил R1 и F раздельно (рис. 4.6). Условие деформации стержня дает:
l = lF + lR |
|
= 0 . |
1 |
|
|
|
R1 |
|
еLR1
|
|
еLF |
EA |
F |
EA |
3EA |
|
3EA |
|
|
|
|
Рис. 4.6 |
|
||||
Подставляя сюда значения |
lF |
|
и |
lR , получим следующее дополни- |
|||||
тельное уравнение: |
|
|
|
|
|
1 |
|
|
|
Fa |
|
|
|
R1a |
|
R1a |
|
|
|
− |
|
+ |
|
+ |
= 0 |
4.18 |
|||
|
|
ΕΑ |
|
||||||
|
3ΕΑ |
|
|
3ΕΑ |
|
||||
Решая совместно уравнения (4.17) и (4.18), получим: |
|
||||||||
|
R1=F/4; |
R 2 = 3 F. |
|
||||||
4
Эпюры N и σ приведены на рис. 4.5 в,г. Величина осевого перемещения сечения на границе участков равна:
w(a)= −4FaΕΑ .
Эпюра осевых перемещений приведена на рис. 4.5, д. Эти перемещения изменяются по линейному закону и в закрепленных сечениях равны пулю. Все поперечные сечения перемещаются вниз.
Пример 2. Рассмотрим статически неопределимую стержневую систему (рис. 4.7, а). Она состоит из абсолютно жесткого горизонтального бруса, шарнирно закрепленного в точке О и подвешенного на двух стержнях. Неизвестными являются (рис. 4.7, б) H, R, N1, N2. В данном случае можно записать только три независимых уравнения равновесия, из которых невозможно определить четыре указанных выше неизвестных усилия.
|
|
76 |
|
|
а) |
l 1 1 |
б) |
|
|
|
|
|
|
|
о |
l 1 2 |
|
N1 |
N2 |
Е1 А 1 в Е2 А 2 c |
H о |
в |
c |
a |
a |
F |
R |
a |
|
a |
F |
|
|
|
в) |
|
о |
в |
|
c |
|
|
|
|
|
|
еl |
2 |
еl |
1 |
|
|
|
|
|
в1 |
|
c1 |
|
|
|
|
|
|
|
|
|
Рис. 4.7
Ограничимся определением усилий N1 и N2 в подвесках. Тогда уравнения равновесия, содержащие только эти неизвестные, запишем так:
∑mo = 0 ; Ν1 a + Ν2 2a − F 2a = 0, или
Ν1 + 2Ν2 = 2F.
(а)
Дополнительное уравнение получим, рассматривая деформацию системы (рис. 4.7, в), в результате которой брус займет положение ОВ1С1. Ввиду малости деформаций считается, что точки В и С перемещаются перпендикулярно к оси бруса, то есть вертикально вниз.
Так как ВВ1 = |
l1 , а СС1 = l2 , то уравнение совместимости в данном |
случае имеет вид |
l2 = 2 l1 . |
Считая деформации упругими и используя закон Гука в форме (4.9), будем иметь:
Ν2l2 = 2 Ν1l1 .
Ε2Α2 Ε1Α1
(б)
Решая совместно уравнения (а) и (б), находим искомые значения усилий
N1 и N2:
Ν1 = |
|
|
|
|
|
|
|
2F |
|
|
|
, |
|
||||||
|
|
|
|
l1 |
|
|
|
|
|
|
|
||||||||
|
1 + 4 |
|
|
|
Ε2 Α2 |
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
l |
2 |
|
|
|
Ε Α |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
||||
|
|
|
4F |
l1 |
|
|
|
Ε2 Α2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
l |
2 |
|
|
|
|
Ε Α |
1 |
|
|
|
|
||||
N2 = |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
. |
(в) |
||||
|
|
|
|
|
l1 |
|
|
|
|
|
|
||||||||
|
|
1 + 4 |
|
|
|
Ε2 Α |
2 |
|
|
|
|||||||||
|
|
|
|
|
Ε Α |
|
|
|
|
||||||||||
|
|
|
|
|
|
l |
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|||
Последние формулы, в частности, показывают, что усилия в стержнях статически неопределимой системы зависят не только от внешней нагрузки и расчетной схемы системы, но и от соотношения жесткостей ее элементов.
