
- •1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
- •1.1. Содержание курса «Сопротивление материалов»
- •1.2. Основные допущения о свойствах материалов и характере деформирования
- •1.3. Геометрическая схематизация элементов конструкций
- •1.4. Классификация нагрузок
- •1.5. Понятие о внутренних силах
- •1.6. Внутренние силы в поперечном сечении бруса
- •1.7. Напряжения. Связь между напряжениями и внутренними силами в поперечном сечении бруса
- •1.8. Понятие о деформациях
- •1.9. Простейшие типы деформации бруса
- •2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
- •2.1. Статические моменты сечений
- •2.2. Моменты инерции сечений
- •2.3. Моменты инерции простейших сечений
- •2.4. Преобразование моментов инерции при параллельном переносе осей
- •2.5. Преобразование моментов инерции при повороте осей
- •2.6. Главные оси инерции. Главные моменты инерции
- •2.7. Моменты сопротивления сечений
- •2.8. Радиусы инерции
- •3. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛ В СЕЧЕНИЯХ СТЕРЖНЕЙ. ЭПЮРЫ ВНУТРЕННИХ СИЛ
- •3.1. Внутренние силы в сечениях бруса (стержнях). Их связь с нагрузкой
- •3.2. Построение эпюр внутренних сил
- •3.3. Построение эпюр внутренних сил в балках
- •3.4. Построение эпюры продольных сил
- •3.5. Построение эпюры крутящих моментов
- •4. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ (ЦРС)
- •4.1. Напряжения деформации при ЦРС. Закон Гука
- •4.2. Определение перемещений при ЦРС
- •4.4. Механические свойства материалов. Диаграммы растяжения и сжатия
- •4.5. Расчет на прочность при растяжении (сжатии)
- •5. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
- •5.1. Напряженное состояние в точке нагруженного твердого тела
- •5.2. Плоское напряженное состояние
- •5.3. Обобщенный закон Гука. Связь между напряжениями и деформациями
- •6. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ (ИЗГИБ БАЛОК)
- •6.1. Определение напряжений в балке
- •6.2. Расчет балок на прочность по допускаемым напряжениям
- •Литература
99
6.2. Расчет балок на прочность по допускаемым напряжениям
Расчет балок на прочность ведется по наибольшим нормальным напряжениям, возникающим в опасном сечении, в котором изгибающий момент имеет наибольшее значение.
|
max М х |
|
σz = |
----------- ≤ [σ] |
(6. 6) |
Wх
Для балок из пластичного материала, у которого допускаемое напряжение на растяжение и сжатие не отличается, наибольшее напряжение берется по абсолютному значению. Для балок из хрупкого материала, у которого допускаемые напряжения на растяжение и сжатие различны, необходимо рассматривать два условия прочности: по наибольшим растягивающим напряжениям и по наибольшим сжимающим напряжениям.
maxσzр ≤ [σ]р , maxσzс ≤ [σ]р |
(6. 7) |
По условиям прочности (6.6) и (6.7) можно решить задачи трех типов: а) Проверочный расчет, когда заданы размеры поперечного сечения и
нагрузка. Проверка прочности сводится к удовлетворению условий (6.6, 6.7).
б) Подбор поперечного сечения, когда заданы нагрузка и известны [σ]. Из условия прочности (6.6) определяется требуемый момент сопротивления поперечного сечения:
max Мх
Wх = |
-----------, |
(6. 6*) |
|
[σ] |
|
по которому определяются размеры заданного поперечного сечения или номер прокатного профиля сечения, имеющий момент сопротивления, равный требуемому или ближайший больший.
в) Определение допускаемой нагрузки (грузоподъемности), когда известны характеристики поперечного сечения и [σ]. Из условия прочности (6. 6) допускаемый изгибающий момент определяется выражением:
[Мх] = [σ] . Wх |
(6. 6*) |
Допускаемая нагрузка определяется по наибольшему изгибающему моменту, выраженному в долях этой нагрузки.
max Мх ≤ [σ] = [σ] Wх
100
Определяющими в оценке прочности балок являются нормальные напряжения, по которым проводится основной расчет. По его выполнении необходима проверка на сдвиг (срез), т.е. на наибольшие касательные напряжения по формуле:
maxQу . SхΩ |
|
maxQу |
|
max τzy = ---------------- |
= |
------------- ≤ [τ] , |
(6. 8) |
yх . вн.сл. |
|
Z 0 . вн.сл. |
|
где maxQу – наибольшее значение поперечной силы для рассматриваемой балки;
[τ] – допускаемое касательное напряжение (обычно [τ] = 0,5[σ]).
Рассмотрим решение некоторых задач.
Задача 1.
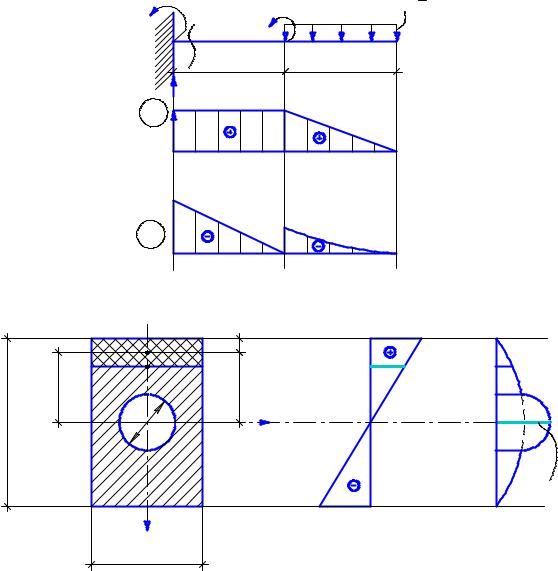
Для деревянной балки, изображенной на рис. 6.6 в сечении 1-1 (у заделки) определить нормальное и касательное напряжение в точке В поперечного сечения и проверить прочность заданной балки, если [σ] = 12Мпа, [τ] = 2МПа.
Решение.
Строим эпюры поперечных сил и изгибающих моментов.
В сечении 1-1, которое совпадает с опасным сечением Qу = 20 кН, Мх = - 20 кНм.
|
|
101 |
|
|
|
МА |
М=10кНм |
q=20мкН |
|
|
1 |
|
|
|
|
1 |
1м |
1м |
|
|
RA |
|
|
|
|
20 |
20 |
|
|
|
Qy |
|
|
|
|
[кН] |
|
|
|
|
20 |
|
|
|
|
Mx |
10 |
|
|
|
|
|
|
|
|
[кНм] |
|
|
|
|
1-1 |
|
Эп.δz |
|
|
|
maxδ |
р |
|
|
|
|
||
|
|
|
z |
|
|
|
5 |
|
|
|
ус |
10 |
|
|
h=30см |
0 |
х |
|
|
|
1 |
|
|
|
|
у |
|
maxδzс |
|
|
в=20см |
|
|
|
|
|
Рис. 6.6 |
|
|
Эп.τzy
τ В |
zy |
maxτzy |
Определим нормальное напряжение в точке В сечения 1-1, предварительно вычислив момент инерции Jх.:
bh3 |
π R4 |
20 . 303 |
π . 54 |
Jх = ----- - |
----- = |
-----------12 - |
--------- = 45000 – 490 . 6 = 44509,4 см4 |
12 |
4 |
4 |
|
Мх |
. уВ = |
-2000 кНсм |
|
σzВ = ------- |
----------------- |
(-10)см = 0,45кН/см2 = 4,5МПа |
|
Jх |
|
44509,4см4 |
|
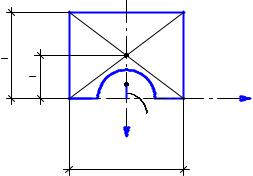
Для определения касательных напряжений в точке В вычислим статический момент отсеченной части площади, расположенной выше точки В.
Sхω = ω. ус = 5 . 20 . 12,5 = 1250 см3
|
|
|
|
102 |
|
|
|
|
|
Qу . │SхΩ│ |
|
20 кН . 1250 см3 |
|
|
|
|
|||
max τzyВ = --------- |
= ------------------------- = 0,028 кН/см2 = 0,28 МПа |
||||||||
Jх . в |
|
44509,4 см4 . 20см |
|
|
|
|
|||
Проверим прочность балки по наибольшим нормальным напряжениям в |
|||||||||
опасном сечении у заделки. |
|
|
|
|
|
|
|
||
|
max│Мх │ |
2000 |
|
|
|
|
|||
max σz = --------------- |
= ---------- = 0,67кН/см2 = 6,7Мпа < [σ] |
||||||||
|
|
Wх |
2967,3 |
|
|
|
|
||
|
|
|
|
Jх |
44509,4 |
|
|
|
|
|
где Wх = ---------- = ------------- = 2967,3см2 |
|
|
||||||
|
|
|
уmax |
15 |
|
|
|
|
|
Условие прочности по наибольшим касательным напряжениям выпол- |
|||||||||
няется. |
|
|
|
|
|
|
|
|
|
Проверим условие прочности по наибольшим касательным напряжени- |
|||||||||
ям, вычислив для этого статический момент части площади поперечного се- |
|||||||||
чения, расположенного по одну сторону от нейтральной оси. |
|
|
|||||||
Sхω1 = ω1 |
|
|
|
bh |
h |
πR2 |
4R |
bh2 |
2 |
. ус1 - ω2 |
. ус2 = ----- . ----- - ------- . ------ = ------ - ----R3 = |
||||||||
|
|
|
|
2 |
4 |
2 |
3π |
8 |
3 |
|
20 . 302 |
2 |
|
|
|
|
|
||
= ----------- - ------ . 53 = 2250 – 83,3 = 2166,7см2 |
|
||||||||
|
8 |
3 |
|
|
|
|
|
||
|
|
вн.с. = b – 2R = 20 – 10 = 10 см |
|
|
|||||
max Qу . Sхω1 |
20 . 1250 |
|
|
|
|
|
|||
max τzyВ = ---------------- = ---------------- = 0,097 кН/см2 = 0,97 Мпа < [τ] |
|||||||||
Jх . в н.с. |
|
44509,4 . 10 |
|
|
|
|
|||
|
2 |
h |
h |
|
с1 |
|
|
|
|
|
|
с2 |
|
|
|
|
|
||
|
|
|
4 |
|
|
х |
|
|
|
|
|
|
|
|
ус |
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
Рис. 6.7 |
|
|
|
|
|
103
т.е. прочность балки обеспечена.
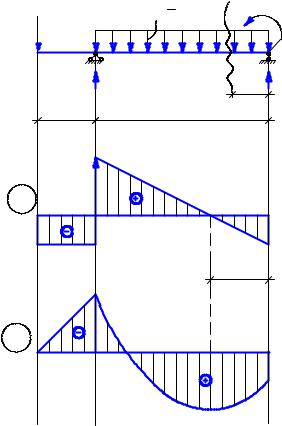
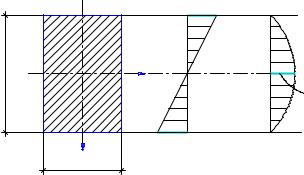
Строим эпюры σz и τzy в сечении 1-1 у заделки.
Задача 2.
Подобрать размеры поперечного сечения балки, изображенной на рис. 6.8, в следующих вариантах:
а) стальную балку двутаврового сечения по таблице сортамента, [σ] = 160 МПа, [τ] = 100 МПа;
б) деревянную балку прямоугольного сечения при h = 2b, [σ] = 12 МПа, [τ] = 2 МПа;
в) деревянную балку круглого сечения при таких же допускаемых напряжениях.
F=20кН |
q=10мкН |
I |
М=20кНм |
|
RA |
z |
RВ |
|
|
1 |
|
|
2м |
6м |
|
|
40 |
|
|
Qy |
|
|
|
[кН] |
20 |
|
20 |
|
|
||
а=2м
40
Mx
[кНм]
20
40
Рис. 6.8
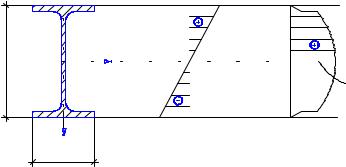
Решение.
Для построения эпюр Qу и Мх находим реакции опор из уравнений рав-
новесия статики:
∑mА = 0 F . 2 – q . 6 . 3 + RB . 6 = 0
|
-40 + 180 - 20 |
RB = ------------------ = 20 кН |
|
|
6 |
∑mB = 0 |
. 8 + q . 6 . 3 + М - RА . 6 = 0 |
|
|
|
|
|
|
|
|
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
160 + 180 + 20 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
RА = -------------------- = 60 кН |
|
||||||||||||||||||||||||
Проверка: |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
+F - RА + q . 6 - RB = 20 – 60 + 60 – 20 = 0. |
||||||||||||||||||||||||||
∑У = 0 |
|
|
|
|
||||||||||||||||||||||||||
Рассмотрим участок балки в пролете, составив для него выражения по- |
||||||||||||||||||||||||||||||
перечной силы и изгибающего момента. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1-й участок 0 ≤ z1 ≤ 6м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Qу = - RB + q . z1 (прямая), |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
q . z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Мх = М + RB . z - ------- |
|
(квадратная пабола) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При z1 = 0 Qу = -20 кН, |
|
|
Мх = 20 кНм, |
|
||||||||||||||||||||||||||
При z1 = 6м Qу = 40 кН, Мх = - 40 кНм. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Найдем экстремальное значения Мх: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Qу/ z1=а = 0, - RB + q . а = 0, |
|
-20 + 10а = 0, |
а = 1 м. |
|||||||||||||||||||||||||||
|
Мх/ z1=2 = 20 + 20 . 2 – 10 . 22 / 2= 40 кНм. |
|||||||||||||||||||||||||||||
2-й участок 0 ≤ z2 ≤ 2м. Qу = -F = -20 кН, |
Мх = -F . z2 = -20z2 . |
|||||||||||||||||||||||||||||
Для подбора сечений берем наибольшие значения поперечной силы и |
||||||||||||||||||||||||||||||
изгибающего момента в опасном сечении балки над опорой А: |
||||||||||||||||||||||||||||||
|
|
|
|
Qу = 40 кН, max Мх = - 40 кНм. |
|
|||||||||||||||||||||||||
а) Определим требуемый момент сопротивления двутавра из условия |
||||||||||||||||||||||||||||||
прочности: |
|
|
|
|
|
|
|
max│Мх │ |
|
|
2000 кНсм |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
max σz ≥ --------------- = --------------- = 250см3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
[σ] |
|
16 кН/см2 |
|
||||||||||||||||||
Принимаем по таблице сортамента (ГОСТ 8239-72) двутавр № 22а, |
||||||||||||||||||||||||||||||
имеющий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wх = 254см3, Jх = 2790см4, Sхпол = 143см3, |
|
|||||||||||||||||||||||||||||
А = 32,8см3 , b = 12см, вн.с. = d = 0,54см. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эп.δz |
|
|
|
Эп.τzy |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
maxδ р |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
||
h=22см |
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
maxτzy |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уmaxδzс
в
Рис. 6.9
105
Проверим условие прочности по наибольшим касательным напряжени-
ям:
max Qу . Sх |
20 кН . 143 см 3 |
|
max τzy = ----------------- |
= |
---------------------- = 3,8 кН/см2 = 38 Мпа < [τ] |
Jх |
. в н.с. |
2790 см 4 . 0,54 см |
т.е. балка удовлетворяет условию прочности по касательным напряжениям.
Строим эпюры σz и τzy в опасном сечении.
б) Определим требуемый момент сопротивления деревянной балки:
|
max Мх |
4000кНсм |
Wх = |
----------- = |
---------------- = 3333 см3 |
|
[σ] |
1,2 кН/см2 |
Для балки прямоугольного сечения момент сопротивления определяется по формуле:
|
bh2 |
b(2b)2 |
2 |
Wх = |
------- = |
--------- = |
----- = 2/3b3, откуда |
|
6 |
6 |
3 |
3 ________
b = √ 3/2 . 3333 = 17,2 см h = 2b = 34,4 см
Проверим условие прочности по наибольшим τ.
maxQу . bh2/8 |
3 |
maxQу |
3 |
40кН |
max τzy = ------------------- = --- . --------- = ---- . ----------------- = |
||||
bh3/12 . b |
2 |
bh |
2 |
17,2 . 34,4см2 |
= 0,1кН/см2 = 1МПа < [τ], |
|
|||
т.е. прочность балки обеспечена. |
|
|
|
|
|
|
Эп.δz |
|
Эп.τzy |
|
|
maxδ |
р |
|
|
z |
|
h |
х |
|
|
|
|
maxτzy |
|
|
|
|
|
у |
maxδ |
с |
|
|
z |
|
|
в |
|
|
|
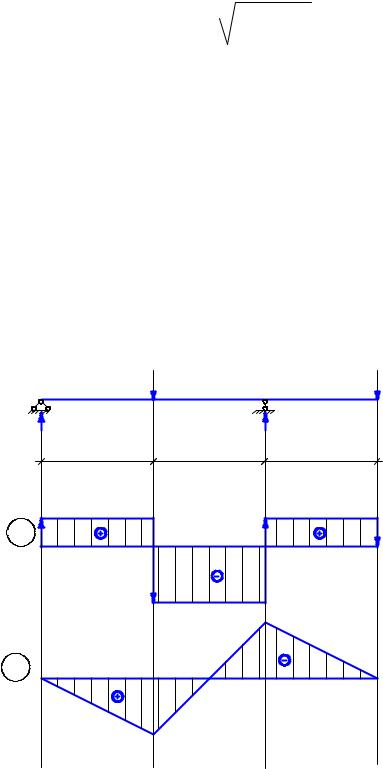
Рис. 6.10
106
Строим эпюры σz и τzy в опасном сечении.
в) Для балки круглого сечения определим диаметр поперечного сечения
при требуемом Wх = 3333 см3. |
|
πd3 |
|
|
|
|
πd3 |
|
|
|
|
|
|
Wх = ----- ≈ 0,1d3 |
; |
------ ≥ 3333 см3 , |
|
откуда |
||
32 |
|
32 |
|
|
|
|
|
3 |
3333 . 32 |
|
|
|
|
|
|
|
|
|
|
|
d ≥ ------------- = 32,1 см |
|
|
||||
Проверим по наибольшим τ. |
π |
|
|
|
|
|
|
|
|
|
|
||
maxQу . 2/3R2 4 |
maxQу |
4 |
maxQу |
4 |
40 |
|
max τzy = ------------------ = --- . --------- = ---- . -------- = --- . -------------- = |
||||||
πR4/4 . 2R |
3 |
πR2 |
3 |
A |
3 |
π . 16,052 |
= 0,066кН/см2 = 0,66 МПа < [τ],
т.е. прочность балки обеспечена.
Задача 3.
Определить допускаемую нагрузку для балки двутаврового сечения (рис. 6. 11) при следующих данных:
двутавр № 30; [σ] = 160 МПа = 16кН/см2; [τ] = 100 МПа.
|
3F |
|
F |
RA |
|
RВ |
|
|
2 |
2 |
2 |
F |
F |
F |
F |
Qy [кН]
2F |
2F |
2F
Mx
[кНм]
2F
Рис. 6.11
107
Решение:
Для построения эпюр Qy и Mx находим реакции опор из уравнений равновесий статики:
∑mА = 0 |
-3F . 2 + RB . 4 – F . 6 = 0 |
|
6F + 6F |
|
RB = ------------ = 3F |
|
4 |
∑mB = 0 |
- RА . 4 + 3F . 2 – F . 2 = 0 |
|
6F – 2F |
|
RA = ----------- = F |
|
4 |
Строим эпюры Qy и Mx.
Опасное сечение в середине пролета max Mx = 2F кНм, max Qy = -2F кН.
Геометрические характеристики для двутавра берем из сортамента:
Wх = 472 см3, Jх = 7080 см4, Sх = 268 см3, в н.с. = d = 0,65 см, в = 13,5 см.
Определим допускаемый изгибающий момент:
[М] = [σ] . Wх = 16 кН/см2 . 472 см3 = 7552 кНсм = 75,52 кНм
Проверим условие прочности по наибольшим τ.
max Qу . Sхωр |
75,52кН . |
268 см3 |
|||||
max τzy = ----------------- |
= ------------------------ |
|
|
= 4,4 кН/см2 = 44 Мпа < [τ] |
|||
Jх . в н.с. |
7080 см4 |
. 0,65 см |
|||||
т.е. прочность балки обеспечена. |
|
|
|
||||
|
|
|
Эп.δz |
Эп.τzy |
|||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h=30см
х
d
maxτzy
|
|
|
у |
maxδzр=[δ] |
|
в
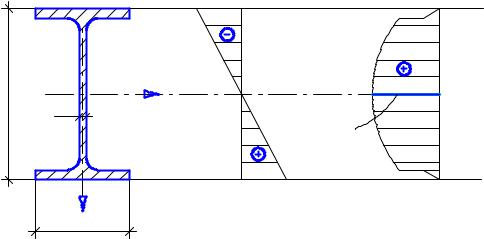
Рис. 6.12
Строим эпюры σz и τzy в опасном сечении (т.к. значения τzy значительно меньше значений σz, то эпюру τzy можно построить в другом масштабе).
