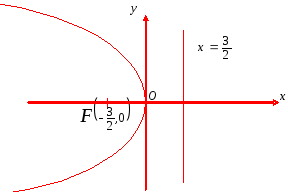
Можно запомнить, что ось симметрии совпадает с переменной входящей в уравнение в первой степени.

Рис. 17

Рис. 18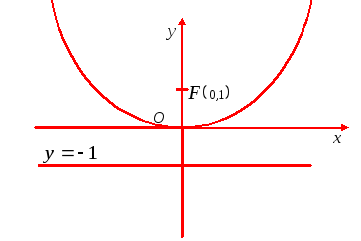

§ 3. Параллельный перенос

Если перенести начало координат в точку и не менять направление осей, то связь между старыми координатами , и новыми , одной и той же точки выражается формулами:

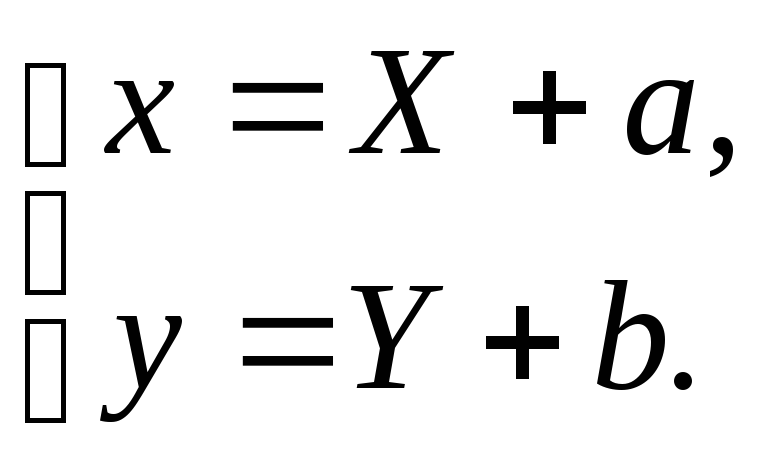или

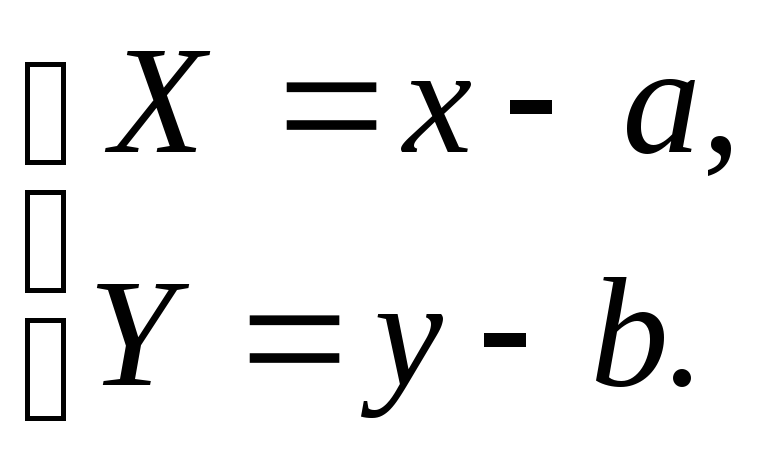
Пример

Установить, что данное уравнение определяет эллипс. Найти координаты его центра, полуоси, эксцентриситет.

Решение:

Перегруппируем слагаемые . Вынесем коэффициент при старших степенях за скобку .

В каждой из полученных скобок добавим слагаемые, так чтобы получился полный квадрат, воспользовавшись формулами сокращенного умножения и .

В нашем случае .

Вынесем за скобки слагаемые, не входящие в полный квадрат

.

Применим формулы сокращенного умножения

. Перенесем свободный член в правую часть.

. Разделим обе части уравнения на 48.

. Произведя сокращение в дробях, получим

.

Введем новые обозначения

Получим . Это каноническое уравнение эллипса в новой системе координат, полученной параллельным переносом старой системы координат, а именно оси на одну единицу вправо, оси на две единицы вниз. Новый центр находится в точке .

Полуоси эллипса равны соответственно и , то есть , значит, фокусы располагаются на оси ординат. Расстояние между фокусами .

Эксцентриситет эллипса равен

.

Пример

Установить, что данное уравнение определяет гиперболу. Найти координаты ее центра, полуоси, эксцентриситет.

Решение:

Перегруппируем слагаемые . Вынесем коэффициент при старших степенях за скобку .

В каждой из полученных скобок добавим слагаемые, так чтобы получился полный квадрат, воспользовавшись формулами сокращенного умножения и .

В нашем случае .

Вынесем за скобки слагаемые, не входящие в полный квадрат

.

Применим формулы сокращенного умножения

Перенесем свободный член в правую часть.

Разделим обе части уравнения на (–144).

. Произведя сокращение в дробях, получим

.

Введем новые обозначения

Получим . Это каноническое уравнение гиперболы в новой системе координат, полученной параллельным переносом старой системы координат, а именно оси на две единицы вправо, оси на одну единицу вниз. Новый центр находится в точке .

Полуоси гиперболы равны соответственно и . Так как знак минус стоит перед , значит, ось есть мнимая ось, а ось – действительная ось, значит, фокусы располагаются на оси ординат. Расстояние между фокусами .

Эксцентриситет гиперболы равен .

§ 4. Плоскость

Пусть в пространстве задана некоторая плоскость P и декартова система координат.

1. Положение плоскости в пространстве однозначно определено, если задана некоторая точка , принадлежащая плоскости Р, и некоторый вектор , перпендикулярный этой плоскости (рис. 20). Пусть – произвольная точка плоскости. Тогда вектор будет перпендикулярен вектору и, следовательно, Так как , , то получим уравнение

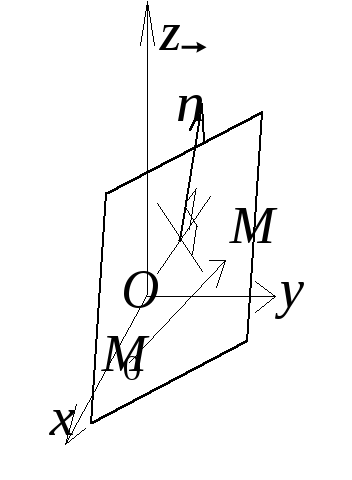
Рис. 20

. (1)

Уравнение (1) есть уравнение плоскости, проходящей через точку перпендикулярно вектору .

Заметим, что вектор называется нормальным вектором плоскости Р.

2. Если в уравнении (1) раскрыть скобки и обозначить: , то получим общее уравнение плоскости:

. (2)

Пусть заданы плоскости P₁: и P₂: . Тогда для того чтобы P₁||P₂ (P₁P₂), необходимо и достаточно, чтобы .

3. Положение плоскости в пространстве также однозначно определено, если заданы три точки , , , принадлежащие плоскости P и не лежащие на одной прямой. Пусть − произвольная точка плоскости. Тогда векторы , , компланарны и .

Так как , , , то последнюю формулу можно переписать в виде

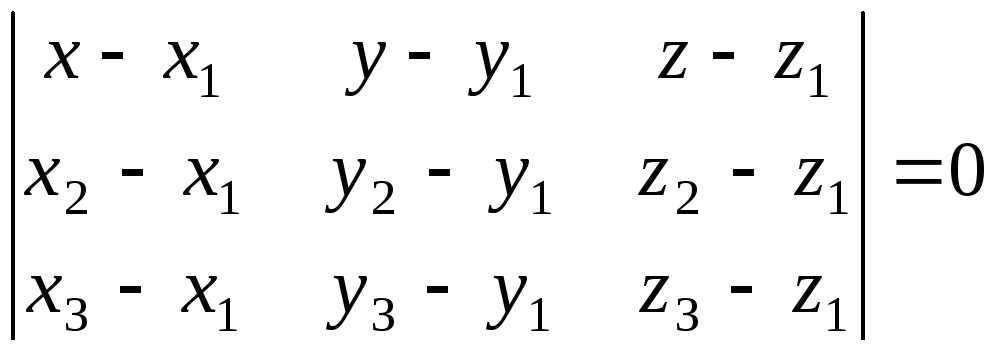. (3)

Уравнение (3) есть уравнение плоскости, проходящей через три известные точки , , .

Пример

Найти угол между плоскостями P и Q, заданными уравнениями и .

Решение:

Угол между плоскостями P и Q равен углу между нормальными векторами этих плоскостей, т.е. между векторами , .

Находим:

,

.