§ 3. Предел функции. Вычисление пределов

Рассмотрим задачи, приводящие к вычислению пределов.

Пример 1

Для наиболее рационального использования леса необходимо знать закономерности увеличения древесной массы в дереве с течением времени. В лесоведении различают два вида прироста: средний и текущий. Текущим приростом в возрасте n лет называют величину , где  объем дерева соответственно в возрасте n и n–1 лет. Средним приростом в возрасте n лет называют величину .

При нормальных условиях средний прирост в первый период жизни возрастает (у хвойных до 50–60 лет), а затем убывает. Докажите, что в период возрастания среднего прироста его величина меньше величины текущего прироста, а затем больше [3].

Доказательство: Справедливость утверждения вытекает из следующего соотношения: .

Пример 2

Бревна и дрова на складах лесоматериалов укладывают в штабеля (штабель с дровами обычно называют поленницей) различной формы. Учет уложенных в штабеля лесоматериалов ведется [27] с помощью коэффициента полнодревесности штабеля, под которым понимается отношение объема древесины в штабеле к геометрическому объему штабеля (первый меньше из-за имеющихся пустот).

Докажите, что значения коэффициента полнодревесности поленницы треугольного профиля, составленной из одинаковых цилиндрических чурок, не выходя из интервала (0,60; 0,91).

Рис. 8

Доказательство: Рассматриваемая поленница (рис. 8) представляет собой «лежащую на боку» правильную треугольную призму. Если в первом ряду поленницы уложено n чурок, то во втором ряду их n–1, в третьем n–2, в последнем 1. Общее количество чурок в поленнице

.

Коэффициент полнодревесности поленницы ,

где l – длина, r– радиус чурки, S – площадь поперечного сечения поленницы, т.е. площадь треугольника ABC. Так как АВ = AD + DE + BE,

, , то.

Следовательно, и

Таким образом, коэффициент полнодревесности поленницы не зависит от радиуса укладываемых чурок, но зависит от их количества, определяемого числом n чурок в первом ряду. Обозначим коэффициент полнодревесности, соответствующий данному n, через и покажем, что последовательность () возрастающая. В самом деле,

,

откуда и вытекает, что .

Для возрастающей последовательности верно соотношение .

У нас . Итак, мы получили для коэффициента полнодревесности оценку снизу: > 0,60.

Для получения оценки сверху заметим, что предел а возрастающей последовательности больше любого члена последовательности: . В нашем случае .

Определение 1. Совокупность действительных чисел

, (1)

расположенных в порядке возрастания номера , называетсячисловой последовательностью, если каждому числу натурального ряда чисел ставится в соответствие некоторое действительное число .

Если функция рассматривается только при целых и положительных значениях аргумента, то она называется функцией натурального аргумента. Таким образом, переменная величина , являющаяся общим членом числовой последовательности (1), зависит от номераи является функцией натурального аргумента, т.е.=().

Пример

Написать первые пять членов последовательности, общий член которой .

Решение:

Придавая аргументу значения 1, 2, 3, 4, 5, получим

; ;;;.

Следовательно, искомая последовательность имеет вид:

, ,,,

Пример

Написать формулу общего члена последовательности

, ,,,

Он имеет вид: .

Определение 2. Число называется пределом последовательности , если для всякого сколь угодно малого положительного числанайдется такое положительное число, чтопри.

В этом случае пишут .

Определение 3. Число называется пределом функции при, если для любого сколь угодно малого положительного числанайдется такое положительное число, чтопри.

В этом случае пишут .

Если , то функцияназываетсябесконечно малой при .

Условно записывают , еслипри, где М –произвольное положительное число. В этом случае функцияназываетсябесконечно большой при .

Если и, то употребляют запись, числоназываетсяпределом слева функции в точке.

Если и, то употребляют запись, числоназываетсяпределом справа функции в точке.

Для существования предела функции принеобходимо и достаточно, чтобы.

Практическое вычисление пределов основывается на следующих теоремах:

Если существуют и, то

1. Предел алгебраической суммы двух (или нескольких) функций равен алгебраической сумме пределов этих функций

.

2. Постоянный множитель можно выносить за знак предела

, где .

3. Предел произведения двух (или нескольких) функций равен произведению пределов этих функций

.

4. Предел частного двух функций равен частному пределов этих функций

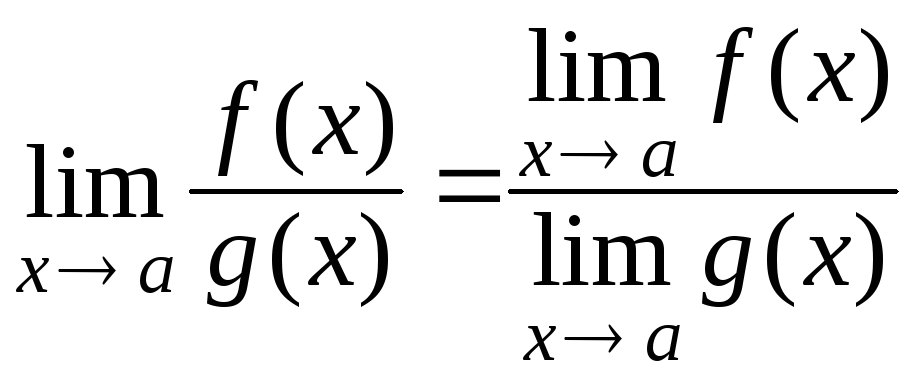(при ).

При вычислениях пределов используются также следующие пределы (а – постоянная, отличная от нуля):

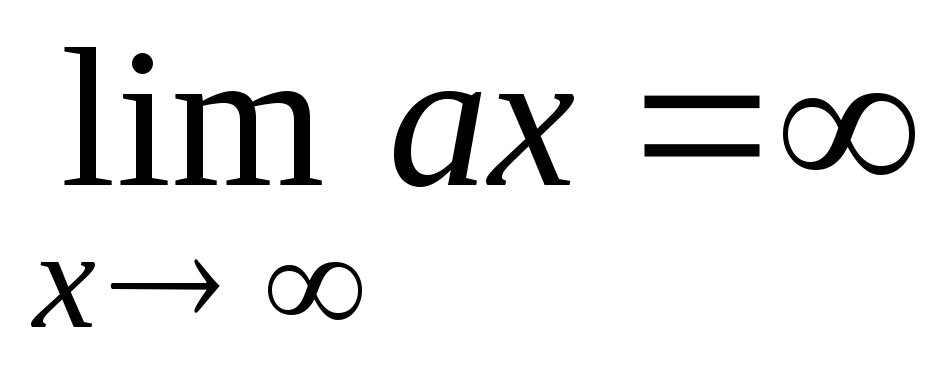1. ; 2) ; 3); 4)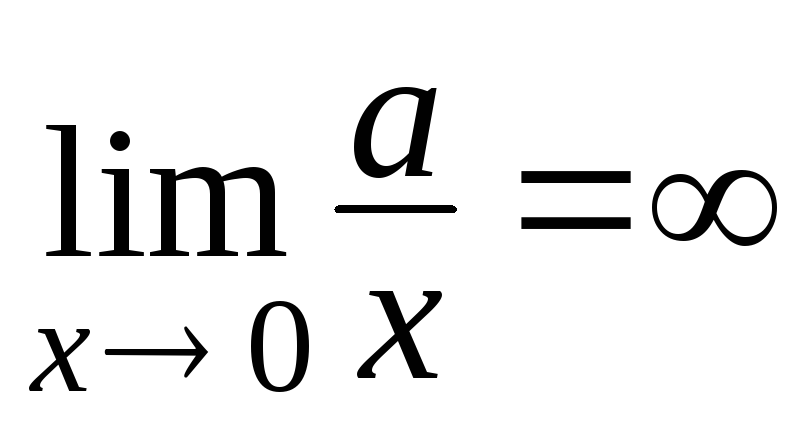

5) Первый замечательный предел:

(есть радианная мера угла).

6) Второй замечательный предел:

.

Для того чтобы найти предел непрерывной функции при, необходимо подставить предельное значение аргументаиз области определения функции в данную функцию и получить значение функции при:

.

Примеры

Найти пределы функций:

1)

так как функция непрерывна в предельной точке , поэтому находим предел функции как частное значение в предельной точке.

2) =.

3) .

Рассмотрим, чему равен предел многочлена при , то есть

Коэффициенты могут быть как положительные, так отрицательные, поэтому возможны случаи, когда под знаком предела будет не сумма (), предел которой, естественно, равен бесконечности, а разность (), предел которой надо отыскать. Вынесем за скобку первое слагаемое многочлена и рассмотрим предел сомножителя, оставшегося в скобках

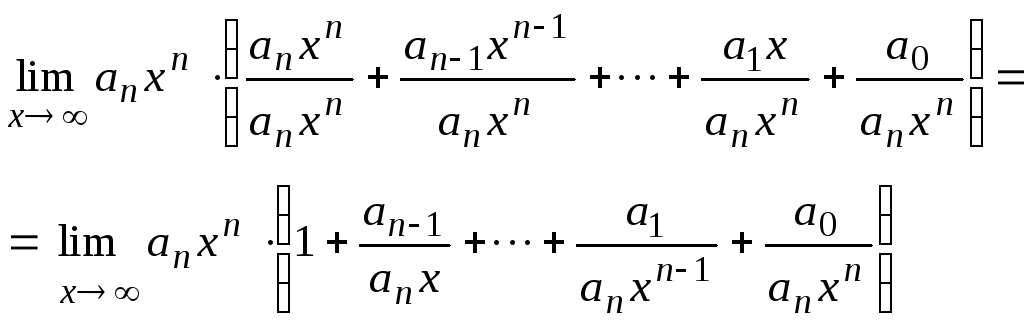
Находим предел выражения, заключенного в скобки

Следовательно, предел многочлена при полностью определяется пределом первого слагаемого

=

На основании этого рассмотрим нахождение предела отношения многочленов при .