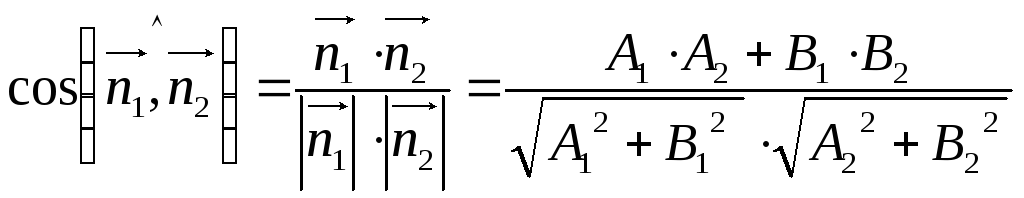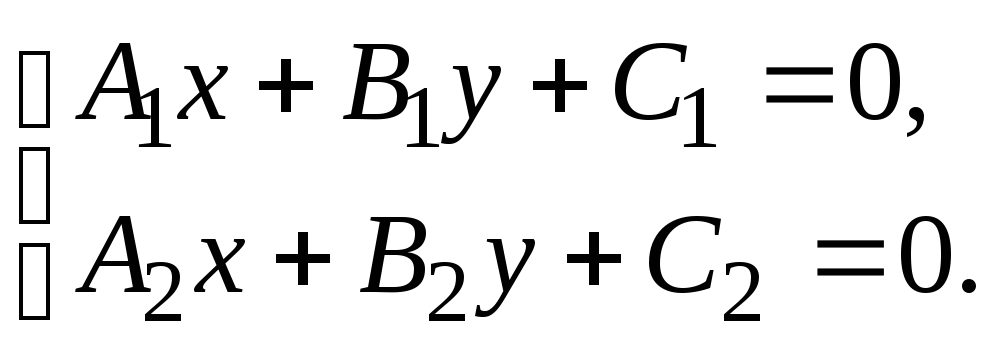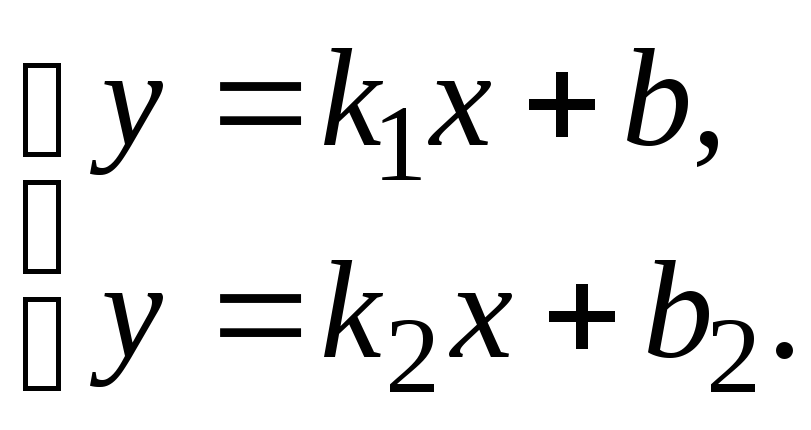Высшая математика / 6_46-53

Пусть заданы прямые l₁: и l₂: . Тогда для того чтобы l₁||l₂ (l₁l₂), необходимо и достаточно, чтобы .

4. Уравнение прямой, проходящей через заданную точку в заданном направлении ()

(4)

5. Положение прямой на плоскости однозначно определено также и в том случае, если известны две точки , через которые проходит прямая. Пусть – произвольная точка прямой. Тогда векторы и коллинеарны, то есть выполняется равенство

(5)

Уравнение (5) определяет прямую, проходящую через две точки .

6. Положение прямой на плоскости однозначно определено, если задана некоторая точка на этой прямой и так называемый направляющий вектор, принадлежащей прямой, параллельной данной. Пусть – некоторая точка прямой l, – ее направляющий вектор. Пусть – произвольная точка прямой. Тогда векторы , коллинеарны, и выполняется равенство =, где  – некоторое действительное число, а также равенства , ; следовательно, и . Уравнение

(6)

определяет прямую, проходящую через известную точку , параллельную направляющему вектору , и называется каноническим уравнением прямой l.

Замечание. Уравнение (6) может быть получено из уравнения (5), если в последнем вектор принять за направляющий вектор.

Расстояние от точки до прямой

Пусть заданы точка и прямая l: . Тогда расстояние от точки M до прямой l (т.е. длина перпендикуляра, опущенного из точки M на прямую l) определяется из следующего соотношения:

. (7)

Взаиморасположение двух прямых

Пусть заданы прямые уравнениями

l1: , l2: , .	l1: l2: .
Угол между прямыми
Равен углу между нормальными векторами данных прямых	и , угол между прямыми можно определить как тангенс разности двух углов Если нужно вычислить острый угол между прямыми l1 и l2., то
Условие параллельности прямых l1||l2
, т.к. их нормальные вектора параллельны	, так как углы наклона прямых к оси равны.
Условие перпендикулярности прямых l1l2
, так как нормальные векторы данных прямых взаимно перпендикулярны	, вытекает из того, что не существует, т.е.
Точка пересечения прямых и аналитически находится путем решения системы уравнений, определяющих эти прямые

Пример

Даны прямые l₁: и l₂: .

А) найти аналитически и графически координаты точки пересечения прямых l₁ и l₂

Б) проверить принадлежит ли точка пересечения прямых и прямым

и ;

В) найти угол между прямыми и .

Решение:

А) Для нахождения точки пересечения двух прямых необходимо составить систему уравнений, описывающих данные прямые. Систему уравнений можно решать разными способами, например, методом Гаусса:

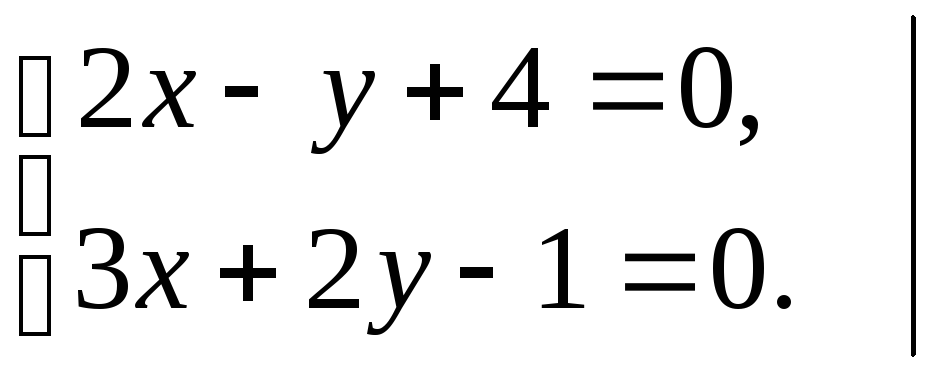2 получаем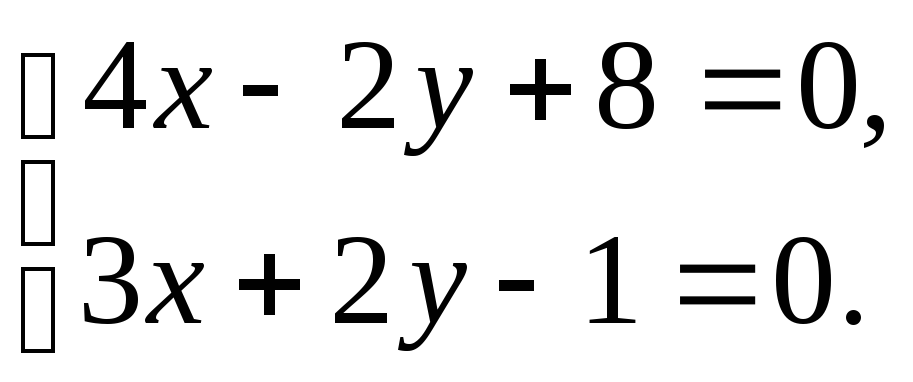

Сложим оба уравнения, получим , откуда или .

Подставив в любое из уравнений системы, получим .

Второй способ решения полученной системы уравнений: можно выделить в каждом из уравнений : и : , а затем приравнять правые части , умножим на 2 обе части уравнения , откуда или . Подставив в любое из уравнений прямых, получим .

Итак, точка пересечения прямых и .

Для того чтобы решить задачу графически, надо прямые и построить на координатной плоскости. Так как через две точки можно провести только одну прямую, найдем по две точки, принадлежащие прямым и .

Для прямой найдем точки пересечения ее с осями координат:

Пусть , тогда или .

Пусть , тогда или .

Таким образом, имеем две точки и .

Для прямой найдем две произвольные точки, задавая произвольные значения одной из переменных, причем желательно задавать такое целое значение одной переменной, чтобы для точности построения вторая переменная имела также целые значения.

П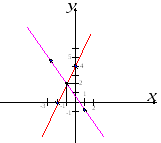усть , тогда , то есть .

Пусть , тогда , то есть .

Т

аким образом, имеем две точки и .

И

Рис. 3

з чертежа видим, что точка пересечения данных прямых , то есть данное решение совпадает с аналитическим.

Б) Для того чтобы проверить, проходит ли прямая через данную точку, достаточно подставить координаты этой точки в уравнение прямой и убедиться, что уравнение обращается в тождество.

В уравнение прямой : подставим координаты точки , получим , откуда , что неверно; значит, точка не принадлежит прямой .

В уравнение прямой : координаты точки , получим откуда , это верно; значит, точка принадлежит прямой .

В) Для нахождения угла  между прямыми и воспользуемся формулой:

В первом случае или

, откуда

Во втором случае . В данном случае необходимо знать угловые коэффициенты прямых и .

l₁: , следовательно, , то есть

l₂: , следовательно, , то есть

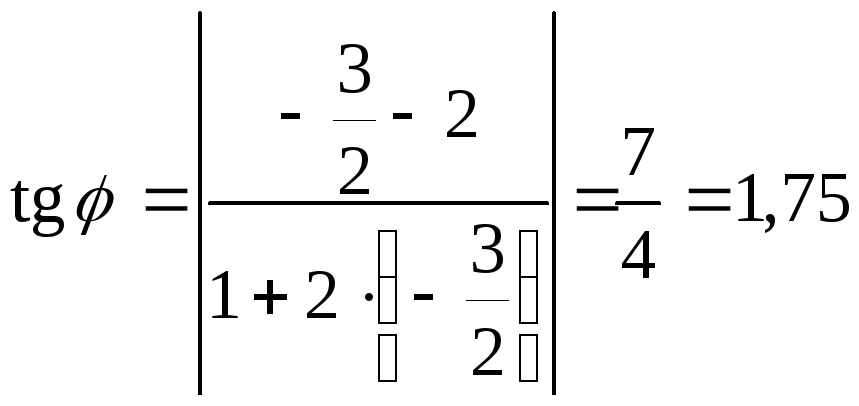, откуда .

=.

При решении контрольной работы угол  достаточно найти одним способом.

Пример

Даны точки, , . Составить уравнения прямых:

А) – проходящей через точки , ;

Б) – проходящей через точку перпендикулярно вектору ;

В) – проходящей через точку параллельно прямой ;

Г) – проходящей через точку перпендикулярно прямой .

Решение:

А) Для составления прямой, проходящей через две заданные точки, воспользуемся формулой: . В нашем случае или , откуда или .

Построим прямую по точке пересечения с осями координат. Убедитесь, что построенная прямая проходит через точки , (для этого подставьте координаты данных точек в уравнение прямой и получите верные равенства).

	0	4
	2	0

Б) Для составления уравнения прямой воспользуемся уравнением прямой в виде .

Найдем

Так как , то за нормальный вектор прямой можем взять , тогда имеет уравнение или .

Построим прямую по любым двум точкам, удовлетворяющим полученному уравнению прямой.

	0	-3
	-1	5

В) Для составления уравнения прямой воспользуемся условием параллельности прямых ||,то есть =1, то есть у параллельных прямых нормальные векторы могут быть равны (а не только пропорциональны).

Таким образом, все прямые, имеющие вид , параллельны прямой , которая имеет уравнение .

Подставив в уравнение координаты точки , найдем с: , откуда . Получаем уравнение прямой : .

Построим прямую , найдя любые две точки, удовлетворяющие уравнению .

	0	3
	5	-1

Г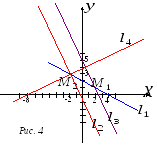) Составить уравнение – проходящей через точку перпендикулярно прямой . Найдем угловой коэффициент прямой , а затем воспользуемся условием перпендикулярности прямых и уравнением . Для этого в уравнении : уединим переменную в левой части .

Коэффициент перед переменной есть угловой коэффициент прямой . Из условия перпендикулярности прямых имеем . Тогда имеет уравнение . Умножим обе части уравнения на 2, получим или уравнение прямой в общем виде .

Построим прямую по уравнению, отыскав точки пересечения с осями координат.

	0	-8
	4	0

§ 2. Кривые второго порядка на плоскости

Кривыми второго порядка называются линии, уравнения которых могут быть записаны следующим образом:

.

где коэффициентыи не могут быть равны нулю одновременно.

52