
Высшая математика / 5_34-45
.doc
Решение:![]()
![]() .
.
Теорема
2. Если
![]() и
и
![]() ,
то
,
то
![]() ,
,
![]() .
.
Пример
Найти
![]() ,
если
,
если
![]() ,
,
![]() .
.
Решение:
![]() .
.
Теорема
3. Если
![]() ,
то
,
то
![]() ,
тогда векторы
,
тогда векторы
![]() и
и
![]() коллинеарны. (См. Теорема 1 § 2, условие
коллинеарности векторов (стр.27)).
коллинеарны. (См. Теорема 1 § 2, условие
коллинеарности векторов (стр.27)).
Условие
коллинеарности векторов:
![]() .
.
Пример
Проверить
коллинеарность векторов
![]() и
и
![]() ,
если
,
если
![]() ,
,
![]()
Решение:
Проверим
условие коллинеарности векторов
![]() ,
имеем
,
имеем
![]() .
Равенства
справедливы, следовательно, векторы
.
Равенства
справедливы, следовательно, векторы
![]() и
и
![]() коллинеарны.
коллинеарны.
Пример
Найти
![]() ,
если
,
если
![]() ,
,
![]() .
.
Решение:
![]() ;
;
![]() .
.
Пусть
,
,
– углы между вектором
![]() и осями Ох,
Oy,
Oz
соответственно (cм. рис. 16).
и осями Ох,
Oy,
Oz
соответственно (cм. рис. 16).
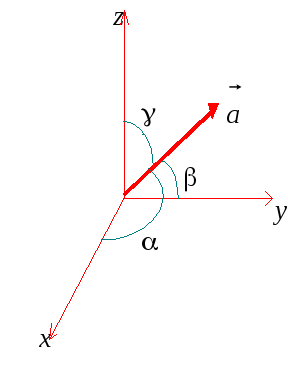 Рис.
16
Рис.
16
Тогда
по свойству 2 проекции вектора на ось
(см. § 3),
![]() ,
,
![]() ,
,
![]() .
.
Определение
3.
cos,
cos,
cos
называются
направляющими
косинусами
вектора
![]() .
.
Теорема
4.
![]() .
.
Деление отрезка в данном отношении
Говорят,
что точка
М
с координатами
x, y, z делит
отрезок
![]()
в
отношении
> 0, если
отношение длин отрезков
![]() и
и
![]() равно
(т.е.
равно
(т.е.![]() ).
).
Теорема
5.
Координаты
точки М, делящей отрезок
![]() в отношении ,
находятся по формулам:
в отношении ,
находятся по формулам:
![]() ,
,
![]() ,
,
![]() .
.
Пример
Для
точек
![]() и
и
![]() найти координаты точки М,
делящей отрезок
найти координаты точки М,
делящей отрезок
![]() в отношении
3 (т.е.
в отношении
3 (т.е.
![]() ).
).
Решение:
Воспользуемся последними формулами, подставив в них числовые данные:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, точка М имеет координаты (0; 2; 1).
§ 6. Скалярное произведение векторов
Определение
1. Скалярным
произведением
![]() векторов
векторов
![]() и
и
![]() называется
называется
число,
равное произведению модулей векторов
![]() и
и
![]() на косинус угла между ними:
на косинус угла между ними:
![]() .
(1)
.
(1)
Отметим,
что если векторы
![]() и
и
![]() перпендикулярны, то их скалярное
произведение равно нулю:
перпендикулярны, то их скалярное
произведение равно нулю:
![]() .
Из определения скалярного произведения
следует, что если
.
Из определения скалярного произведения
следует, что если
![]() острый, то
острый, то
![]() ;
если
;
если
![]() тупой, то
тупой, то
![]() .
Из (1) вытекает, что
.
Из (1) вытекает, что
![]() .
Заметим также, что в силу свойства
проекции вектора на ось или вектор
справедливо равенство
.
Заметим также, что в силу свойства
проекции вектора на ось или вектор
справедливо равенство
![]() .
.
Некоторые свойства скалярного произведения
1.
![]()
2.
![]()
3.
![]()
4.
![]()
![]()
![]()
Теорема
1.
Скалярное
произведение векторов
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
![]() .
.
Тогда свойство 4 (условие перпендикулярности векторов) имеет вид
![]() .
.
Скалярное произведение позволяет находить угол между векторами,
координаты которых известны. Из определения скалярного произведения имеем:
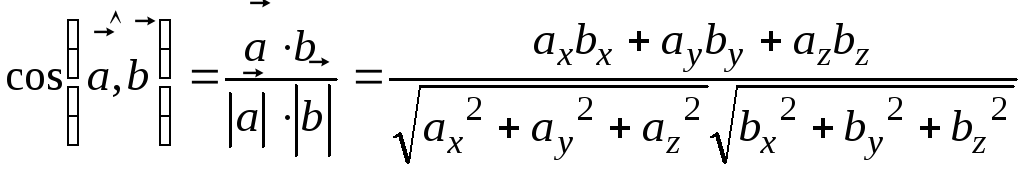 .
.
Пример
Даны
точки
![]() ,
,
![]() ,
,
![]() .
Найти координаты и модуль вектора
.
Найти координаты и модуль вектора
![]() и угол
и угол
![]() между векторами
между векторами
![]() и
и
![]() .
.
Решение:
Найдём
координаты векторов
![]() ,
,
![]() и
и
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Найдем
координаты вектора
![]() :
:
![]()
Найдем
модуль вектора
![]() :
:
![]() .
.
Найдем
косинус
![]() =
=
![]() :
:
![]()
![]() .
.
Построение
П остроим
точки
остроим
точки
![]() .
Из точки
.
Из точки
![]() построим вектор
построим вектор
![]() ,
из точки
,
из точки
![]() построим вектор
построим вектор
![]() ,
соединив точки
,
соединив точки
![]() и
и
![]() ,
получим искомый вектор
,
получим искомый вектор
![]() .
.
Таким
образом,
![]() ,
,
![]() ,
тогда
,
тогда
![]()
П остроение
можно сделать по-другому (зависит от
удобства построения). В начало координат
поместим начало вектора
остроение
можно сделать по-другому (зависит от
удобства построения). В начало координат
поместим начало вектора
![]() и начало вектора
и начало вектора
![]() ,
тогда
,
тогда
![]() .
.
§ 7. Векторное произведение векторов
Определение.
Векторным
произведением
![]() векторов
векторов
![]() и
и
![]() называется вектор
называется вектор
![]() (рис.
17) такой, что:
(рис.
17) такой, что:
1)
![]() ;
;
2)
![]() перпендикулярен
к плоскости векторов
перпендикулярен
к плоскости векторов
![]() и
и
![]() ;
;
3)
![]() образует с упорядоченной парой векторов
образует с упорядоченной парой векторов
![]() и
и
![]() правую тройку (т.е. если смотреть с конца
вектора
правую тройку (т.е. если смотреть с конца
вектора
![]() на плоскость векторов
на плоскость векторов
![]() и
и
![]() ,
то кратчайший поворот от вектора
,
то кратчайший поворот от вектора
![]() к вектору
к вектору
![]() происходит против часовой стрелки).
происходит против часовой стрелки).
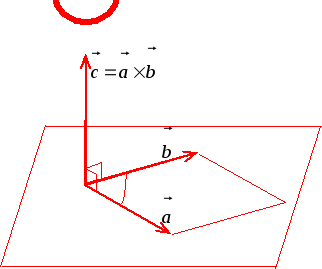
Рис. 17
Геометрический
смысл векторного произведения:
Модуль
векторного произведения
![]() численно
равно площади параллелограмма,
построенного на векторах
численно
равно площади параллелограмма,
построенного на векторах
![]() и
и
![]() .
.
Из определения векторного произведения следует (см. рис. 18), что
![]() .
.
![]() Рис.
18
Рис.
18
Теорема.
Векторное
произведение векторов
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
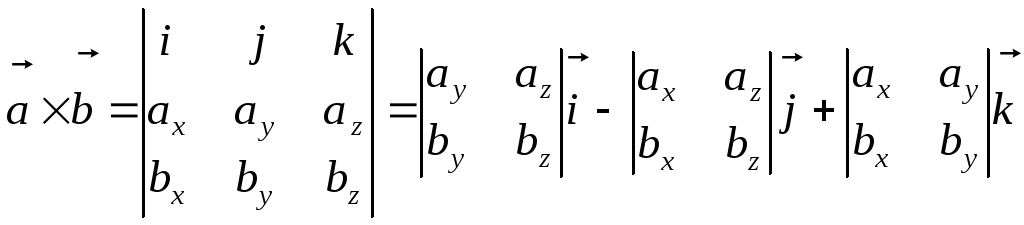 .
.
§ 8. Смешанное произведение векторов
Определение.
Смешанным произведением векторов
![]() ,
,
![]() и
и
![]() называется число,
равное скалярному произведению вектора
называется число,
равное скалярному произведению вектора
![]() на вектор
на вектор
![]() или
вектора
или
вектора
![]() на
вектор
на
вектор
![]() .
.
Будем
обозначать:
![]() .
.
Геометрический
смысл смешанного произведения: Модуль
смешанного произведения
![]() равен объёму параллелепипеда, построенного
на векторах
равен объёму параллелепипеда, построенного
на векторах
![]() ,
,
![]() и
и
![]() .
.
Действительно,
обозначим через H
основание перпендикуляра, опущенного
из точки А
на плоскость
![]() (см. рис. 19). Тогда
(см. рис. 19). Тогда
![]()
![]() .
.
Теорема
1.
![]() тогда и
только тогда, когда векторы
тогда и
только тогда, когда векторы
![]() ,
,
![]() и
и
![]() компланарны.
компланарны.

Рис. 19
Теорема
2.
Пусть
![]() ,
,
![]() ,.
Тогда
,.
Тогда
![]()
 .
.
Пример
Найти объём пирамиды АВСD, где А(2;-3;1), В(4;7;0), С(5;5;-7), D(1,1,1).
Решение:
Найдём координаты векторов
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Из
школьной программы по геометрии известно,
что объём тетраэдра, построенного на
векторах
![]() ,
есть одна шестая часть параллелепипеда,
построенного на этих векторах. Поэтому,
в силу теоремы 2,
,
есть одна шестая часть параллелепипеда,
построенного на этих векторах. Поэтому,
в силу теоремы 2,
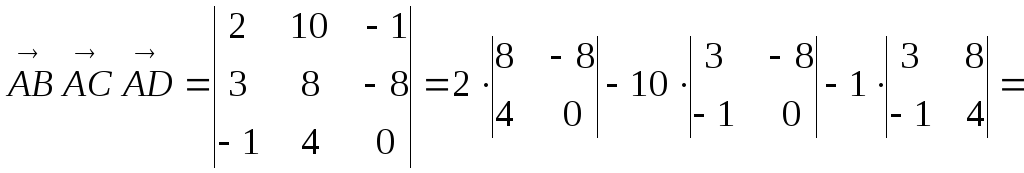
=
![]()
![]()
Глава 3. Элементы аналитической
геометрии
Аналитическая геометрия – раздел математики, изучающий геометрию методами алгебры, то есть геометрические объекты описываются уравнениями.
Уравнением
линии на плоскости называется уравнение,
связывающее
![]() и
и
![]() ,
которому удовлетворяют координаты
любой точки линии и не удовлетворяют
координаты ни одной точки, не лежащей
на линии.
,
которому удовлетворяют координаты
любой точки линии и не удовлетворяют
координаты ни одной точки, не лежащей
на линии.
§ 1. Прямая на плоскости
Пусть на плоскости задана некоторая прямая l и декартова система координат.
1.
Положение прямой l
на плоскости однозначно определено,
если задана некоторая точка
![]() ,
принадлежащая прямой l,
и некоторый вектор
,
принадлежащая прямой l,
и некоторый вектор
![]() ,
перпендикулярный этой прямой (рис. 1).
,
перпендикулярный этой прямой (рис. 1).
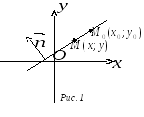
Пусть
![]() – произвольная точка прямой. Тогда
вектор
– произвольная точка прямой. Тогда
вектор
![]() будет перпендикулярен вектору
будет перпендикулярен вектору
![]() и, следовательно,
и, следовательно,
![]() .
Так как
.
Так как
![]() ,
,
![]() ,
то получим уравнение
,
то получим уравнение
![]() . (1)
. (1)
Отметим,
что вектор, перпендикулярный данной
прямой, называется нормальным
вектором
этой прямой. Уравнение (1) есть уравнение
прямой, проходящей через точку М0
перпендикулярно нормальному вектору
![]() .
.
2.
Если в
уравнении (1) раскрыть скобки и обозначить:
![]() ,
то получим общее
уравнение прямой:
,
то получим общее
уравнение прямой:
![]() . (2)
. (2)
Пусть
заданы прямые l1:
![]() и l2:
и l2:
![]() .
Тогда для того чтобы l1||l2
(l1l2),
необходимо и достаточно, чтобы
.
Тогда для того чтобы l1||l2
(l1l2),
необходимо и достаточно, чтобы
![]()
![]() .
.
3.
В уравнении (2) выразим переменную y,
то есть
![]() .
Введя новые обозначения
.
Введя новые обозначения
![]() ,
получим уравнение
прямой с угловым коэффициентом
,
получим уравнение
прямой с угловым коэффициентом
![]() , (3)
, (3)
известное
из школьной программы как уравнение
линейной функции (графиком которой
является прямая). Здесь
![]() ,
– угол между прямой и положительным
направлением оси Ох,
b
– ордината точки пересечения прямой и
оси Оу
(cм.
рис. 2).
,
– угол между прямой и положительным
направлением оси Ох,
b
– ордината точки пересечения прямой и
оси Оу
(cм.
рис. 2).
