2) Дисперсию ;

3) Среднее квадратическое отклонение .

4) Построить многоугольник распределения;

5) Построить функцию распределения.

361. 362.

Х	-6	8	9	10		Х	-2	0	1	4
р	0,1	0,1	0,6	0,2		р	0,5	0,1	0,2	0,2

363. 364.

Х	-2	-1	0	3		Х	-1	0	1	3
р	0,2	0,5	0,1	0,2		р	0,4	0,4	0,1	0,1

365. 366.

Х	-5	-4	-2	3		Х	-1	2	4	8
р	0,1	0,5	0,2	0,2		р	0,2	0,5	0,1	0,2

367. 368.

Х	-6	-3	2	1		Х	-8	-6	-1	5
р	0,3	0,3	0,2	0,2		р	0,5	0,1	0,3	0,1

369. 370.

Х	-4	-2	1	3		Х	-2	0	1	3
р	0,1	0,3	0,2	0,4		р	0,1	0,1	0,3	0,5

371. 372.

Х	-7	-2	2	3		Х	-4	-1	3	5
р	0,1	0,3	0,2	0,4		р	0,1	0,6	0,2	0,1

373. 374.

Х	-5	-2	3	7		Х	-3	-1	0	2
р	0,1	0,3	0,2	0,4		р	0,3	0,2	0,3	0,2

375. 376.

Х	0	2	4	5		Х	-3	0	2	7
р	0,1	0,2	0,2	0,5		р	0,1	0,6	0,2	0,1

377. 378.

Х	-5	1	2	4		Х	-3	2	4	6
р	0,2	0,3	0,1	0,4		р	0,1	0,7	0,1	0,1

379. 380.

Х	1	3	4	5		Х	-3	-1	1	3
р	0,4	0,3	0,2	0,1		р	0,2	0,1	0,2	0,5

В задачах 381- 400 Случайная величина задана функцией распределения вероятностей. Найти:

1) Вероятность попадания случайной величины в интервал;

2) плотность распределения вероятностей случайной величины ;

3) математическое ожидание ;

4) дисперсию .

381. 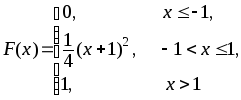382.

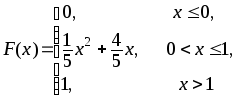
383. 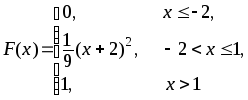384.

385. 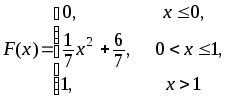386.

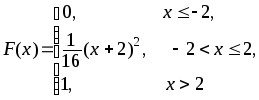
387. 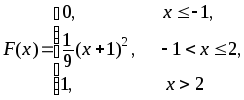388.

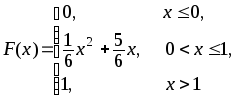
389. 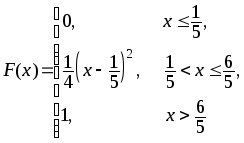390.

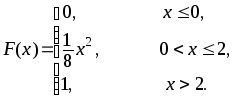
391. 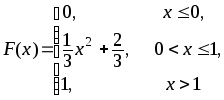392.

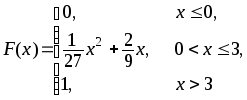
393. 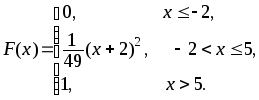394.

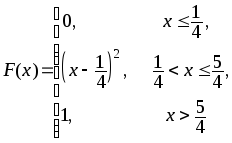
395. 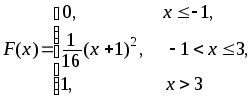396.

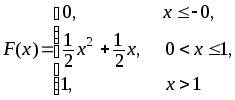
397. 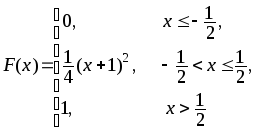398.

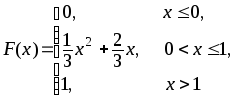
399. 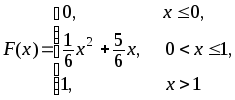400.

В задачах 401-420 дано, что детали выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали (математическое ожидание) равна мм, среднее квадратическое отклонение -мм. Найти:

1) вероятность того, что диаметр наудачу взятой детали будет больше мм и меньшемм;

2) вероятность того, что диаметр наудачу взятой детали отклонится от стандартной длины не более чем на мм.

401. ,,,,.

402. ,,,,.

403. ,,,,.

404. ,,,,.

405. ,,,,.

406. ,,,,.

407. ,,,,.

408. ,,,,.

409. ,,,,.

410. ,,,,.

411. ,,,,.

413. ,,,,.

413. ,,,,.

414. ,,,,.

415. ,,,,.

416. ,,,,.

417. ,,,,.

418. ,,,,.

419. ,,,,.

420. ,,,,.

255