Высшая математика / 14_171-179

Определение 2. Дискретной случайной величиной называется величина, число возможных значений которой либо конечно, либо бесконечное счетное множество, все возможные значения которого могут быть занумерованы с помощью натурального ряда чисел.

Определение 3. Законом распределения ДСВ называется соответствие, устанавливающее связь между возможными значениями случайной величины и вероятностями появления этих значений.

Зная закон распределения вероятностей, можно до опыта судить о том, какие значения случайной величины будут появляться чаще, какие реже.

Способы и формы представления законов распределения могут быть различными. Закон распределения можно задавать таблично, аналитически и графически. При табличном задании в первой строке таблицы перечисляются все возможные значения случайной величины, а во второй – соответствующие им вероятности.

			...
			...

Заметим, что сумма вероятностей всех возможных значений равна . Действительно, события , , ..., попарно несовместны, а их сумма является достоверным событием, так как в результате осуществления комплекса условий случайная величина принимает одно из ее возможных значений. Поэтому . По формуле сложения вероятность суммы несовместных событий равна сумме вероятностей каждого из этих событий. Таким образом, Это свойство закона распределения называется свойством нормировки.

При аналитическом задании закона распределения задается формула для вычисления вероятностей того, что примет значение, равное . Например, формулы Бернулли задают закон распределения случайной величины – числа появления события A в серии из испытаний. Возможными значениями случайной величины являются числа 0, 1, 2,..., , а вероятности этих значений находят по формулам

, где .

Закон распределения, в котором вероятности возможных значений вычисляются по формулам Бернулли, называют биномиальным.

При графическом задании на одной оси откладываются значения случайной величины, а на другой – вероятности этих значений. Точки соединяются отрезками прямых и полученную фигуру называют многоугольником распределения. Многоугольник распределения дает наглядное представление о распределении вероятностей возможных значений случайной величины.

§ 8. Числовые характеристики ДСВ

I. Математическое ожидание ДСВ

Определение 1. Математическим ожиданием ДСВ называют число, равное сумме произведений всех возможных значений случайной величины на вероятности этих значений

=

Свойства математического ожидания

Пусть _, – случайные величины, а – постоянная величина, тогда математическое ожидание обладает следующими свойствами:

1.

2.

3.

4. , если и – независимые ДСВ.

5. Если  , то

II. Дисперсия и среднее квадратическое отклонение ДСВ

Определение 2. Дисперсией случайной величины называют число равное математическому ожиданию квадрата отклонения случайной величины от её математического ожидания.

Дисперсия может быть вычислена по формуле

Размерность дисперсии равна квадрату размерности , поэтому вводят ещё одну характеристику разброса с той же размерностью, что и , которая называется средним квадратическим отклонением .

Свойства дисперсии

Пусть _, – независимые случайные величины, а – постоянная величина, тогда дисперсия обладает следующими свойствами:

1.

2.

3. , .

Пример

Найти дисперсию ДСВ _, заданной законом распределения

	1	2	3
	0,25	0,5	0,25

Решение:

1 способ. Вычислим сначала математическое ожидание этой случайной величины. По определению .

Для вычисления дисперсии по определению составим закон распределения случайной величины .

	1	0	1
	0,25	0,5	0,25

Вычислим математическое ожидание этой случайной величины.

.

По определению это число и является дисперсией. Таким образом, .

2 способ. Вычислим дисперсию по формуле . Уже подсчитано, что , поэтому .

Составим закон распределения .

	1	4	9
	0,25	0,5	0,25

Найдем , тогда

.

§ 9. Непрерывные случайные величины

Определение 1. Непрерывной случайной величиной (НСВ) называется такая величина, все возможные значения которой заполняют сплошь некоторый интервал числовой оси (конечный или бесконечный).

Так как все возможные значения НСВ невозможно занумеровать, то закон распределения НСВ нельзя задать в виде таблицы, поэтому необходим новый способ задания закона распределения вероятностей.

I. Функция распределения вероятностей

Определение 2. Функцией распределения случайной величины называется функция , которая для каждого значения аргумента равна вероятности того, что при испытании случайная величина примет значение меньшее, чем , то есть .

Иногда вместо термина функция распределения пользуются термином интегральная функция распределения.

Свойства функции распределения

1. Из определения функции распределения непосредственно следует, что .

2. – неубывающая функция, то есть если , то .

3.

Если возможные значения случайной величины принадлежат интервалу , то

1. при _;

2. при .

На рис. 1 изображен график функции распределения некоторой случайной величины , возможные значения которой принадлежат интервалу .

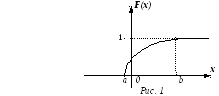
II. Дифференциальная функция распределения вероятностей (плотность вероятности).

Определение 3. Плотностью вероятности непрерывной случайной величины называется функция , обладающая следующими свойствами: 1.

2. 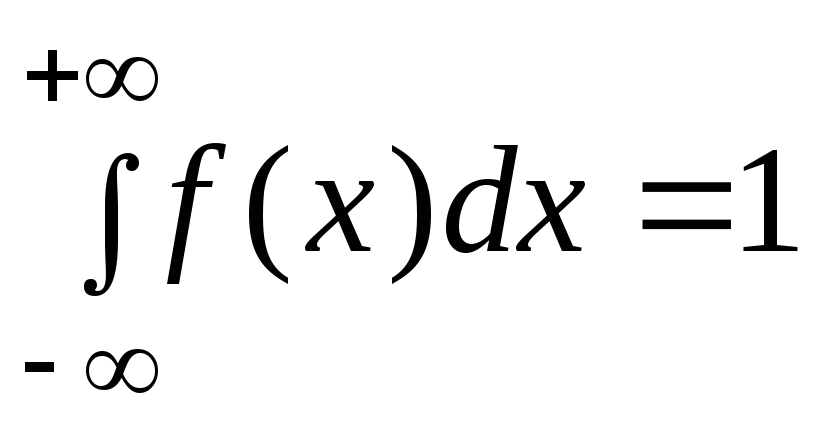при и при .

3. .

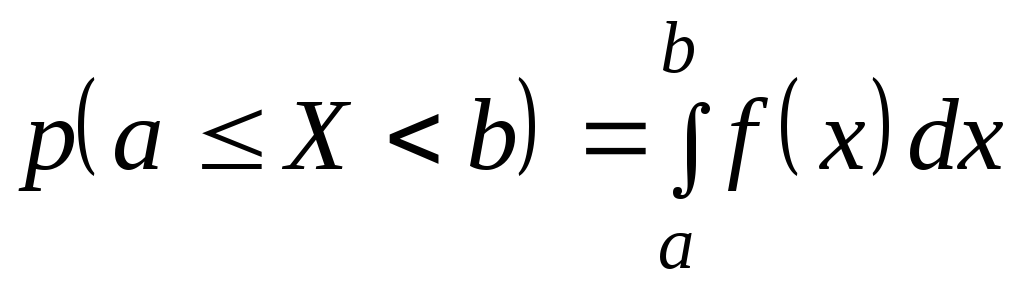График плотности вероятности называется кривой распределения. Кривая распределения располагается либо выше оси Ох, либо на некоторых участках совпадает с ней. Геометрически свойство 2 (нормировки) означает, что площадь под кривой распределения равна 1, а свойство 3 означает, что вероятность попадания значения случайной величины в заданный интервал на оси равна площади криволинейной трапеции, ограниченной сверху кривой распределения, основанием которой является данный интервал.

Определение 4. Математическим ожиданием НСВ называется несобственный интеграл

Замечание. Несобственным интегралом называется интеграл с бесконечными пределами интегрирования.

Определение 5. Дисперсией НСВ называют математическое ожидание квадрата её отклонения от математического ожидания .

Определение 6. Средним квадратическим отклонением НСВ называется .

§ 10. Законы распределения непрерывных случайных величин

1. Равномерное распределение

Определение. Распределение вероятностей НСВ , принимающей все свои значения из отрезка называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, то есть

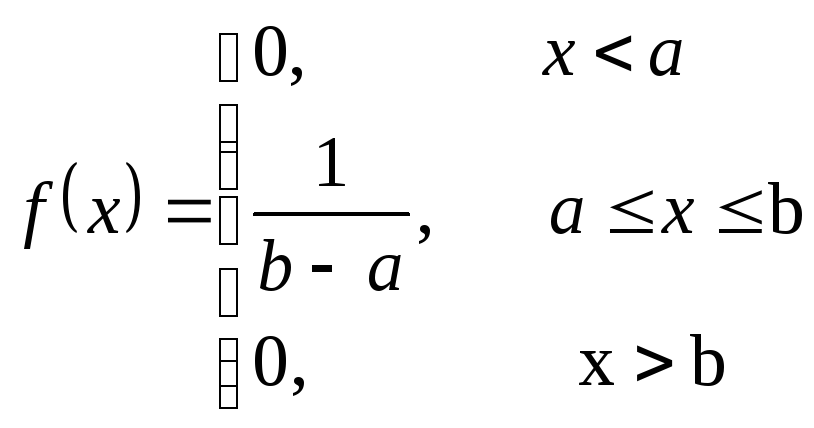
Функция распределения равномерного закона

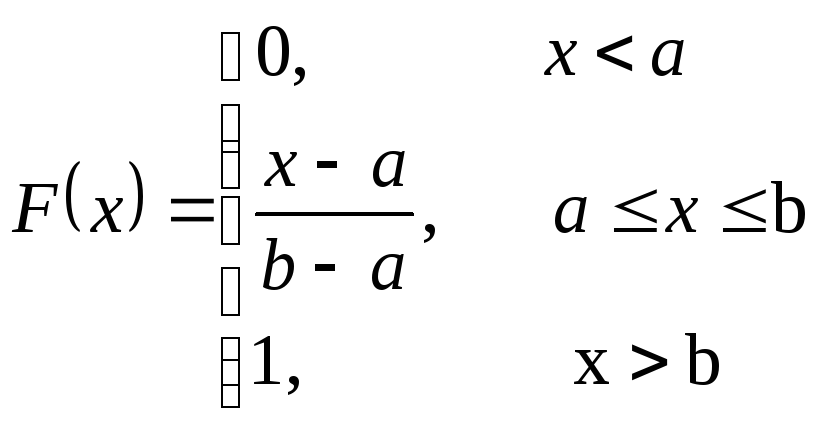
Вероятность попадания в интервал непрерывной случайной величины , распределенной по равномерному закону .

Математическое ожидание, дисперсия и среднее квадратическое отклонение равномерного распределения соответственно равны:

, , .

2. Показательное распределение

Определение. Закон распределения вероятностей непрерывной случайной величины называется показательным, если ее плотность вероятности определяется формулой

где – постоянная положительная величина.

Функция распределения показательного закона

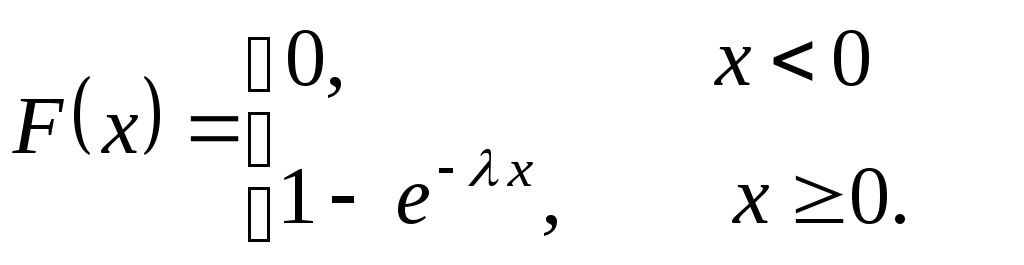
Вероятность попадания в интервал непрерывной случайной величины , распределенной по показательному закону .

Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:

, , .

3. Нормальное распределение

Определение. Закон распределения вероятностей непрерывной случайной величины называется нормальным, если ее плотность вероятности

определяется формулой , где , .

Вероятность того, что случайная величина примет значение, принадлежащее интервалу , вычисляется по формуле

,

где – функция Лапласа. Таблица функции Лапласа для положительных значений () приведена в приложении 2. Для значений полагают . Для отрицательных значений учитывают, что функция Лапласа нечетная .

Вероятность того, что абсолютная величина отклонения меньше положительного числа , то есть или, раскрывая модуль, , вычисляется по формуле

, таким образом, .

Правило трех сигм

Если случайная величина имеет нормальное распределение, то практически достоверно, что абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

.

Таким образом, событие или практически достоверно.

Пример

В парке растут липы одного года посадки. Средний диаметр их стволов на высоте 1метр равен 40 мм. Будем считать, что диаметр ствола есть НСВ распределенная по нормальному закону со средним квадратическим отклонением мм. Найти:

1) вероятность того, что диаметр наудачу измеренного ствола липы будет больше 34 мм и меньше 43мм;

2) вероятность того, что диаметр наудачу измеренного ствола липы отклонится от его математического ожидания не более чем на 1,5 мм.

3) с помощью правила трех сигм найти границы, в которых будет находиться диаметр наудачу измеренного ствола липы.

Решение:

1) Так как диаметр наудачу измеренного ствола липы - НСВ , распределенная по нормальному закону, то средний диаметр является математическим ожиданием НСВ , т.е. . Применим формулу для вычисления вероятности попадания НСВ в заданный интервал, т.е.

где – функция Лапласа, , .

В задаче , , , . Тогда

2) По условию задачи , где , .

. Тогда

3) Практически достоверно, что диаметр ствола липы заключен в границах от мм до мм, то есть .

179